Control and Redundancy in Network Dynamics
The paradigmatic example of a complex system is the web of biochemical interactions that make up life. We still know very little about the organization of life as a dynamical, interacting network of genes, proteins and biochemical reactions. How do biochemical networks—containing many regulatory, signaling, and metabolic processes—achieve reliability and robustness while evolving? Cells function reliably despite noisy dynamic environments, which is all the more impressive given that control strategies implemented by intra and inter-cellular processes cannot rely on a centralized, global view of the relevant networks. Are the resulting complex dynamics made up of relatively autonomous modules? If so, what is their functional role and how can they be identified? How robust is the collective computation performed by intra-cellular networks to mutations, delays and stochastic noise? To address these questions, we are focused on developing both novel methodologies and informatics tools to study control and collective computation in automata networks used to model gene regulation and biochemical signaling.
Network science has provided many insights into the organization of complex systems. The success of this approach is its ability to capture the organization of multivariate interactions as networks or graphs without explicit dynamical rules for node variables. As the field matures, however, there is a need to move from understanding to controlling complex systems; for example, to revert a diseased cell to a healthy state, or a mature cell to a pluripotent state. This is particularly true in systems biology and medicine, where increasingly accurate models of biochemical regulation have been produced. We have contributed to this goal with two mathematical concepts which allow us to remove different forms of redundancy in networks: 1) distance closures, and 2) canalization via schema re-description. The latter concept is used to remove redundancy from the logical rules of biochemical regulation models in systems biology, revealing that most variables (e.g. chemical species) rely on a smaller subset of their inputs to be regulated (canalization). The removal of this redundancy simplifies and indeed enables the causal and actionable characterization of control in large biochemical and neural network models, which are otherwise too large to study analytically [Rocha , 2022].
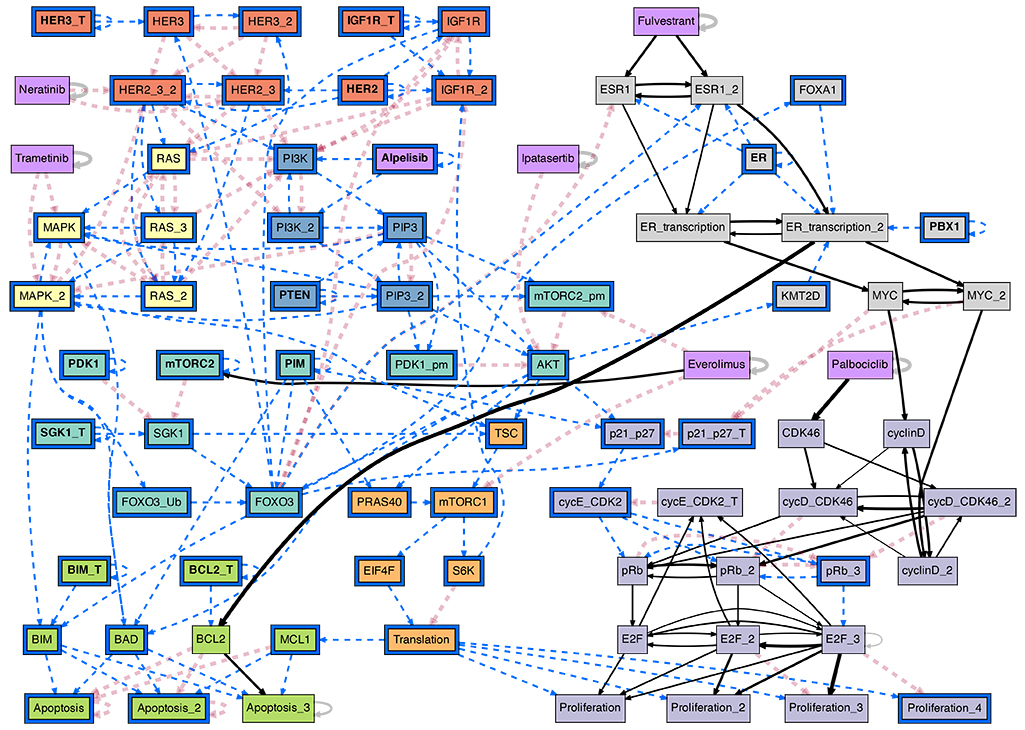
The conditional effective graph of the ER+ breast cancer BN model, conditioned on the ER+/Her2- cancer cell state baseline plus the PI3K inhibitor Alpelisib. This probabilistic causal graph reveals canalization in the biochemical regulation of pharmacological interventions in Cancer; it allows the study of actionable interventions in treatment and disease progression. (see [Gates et al, 2021] for details)
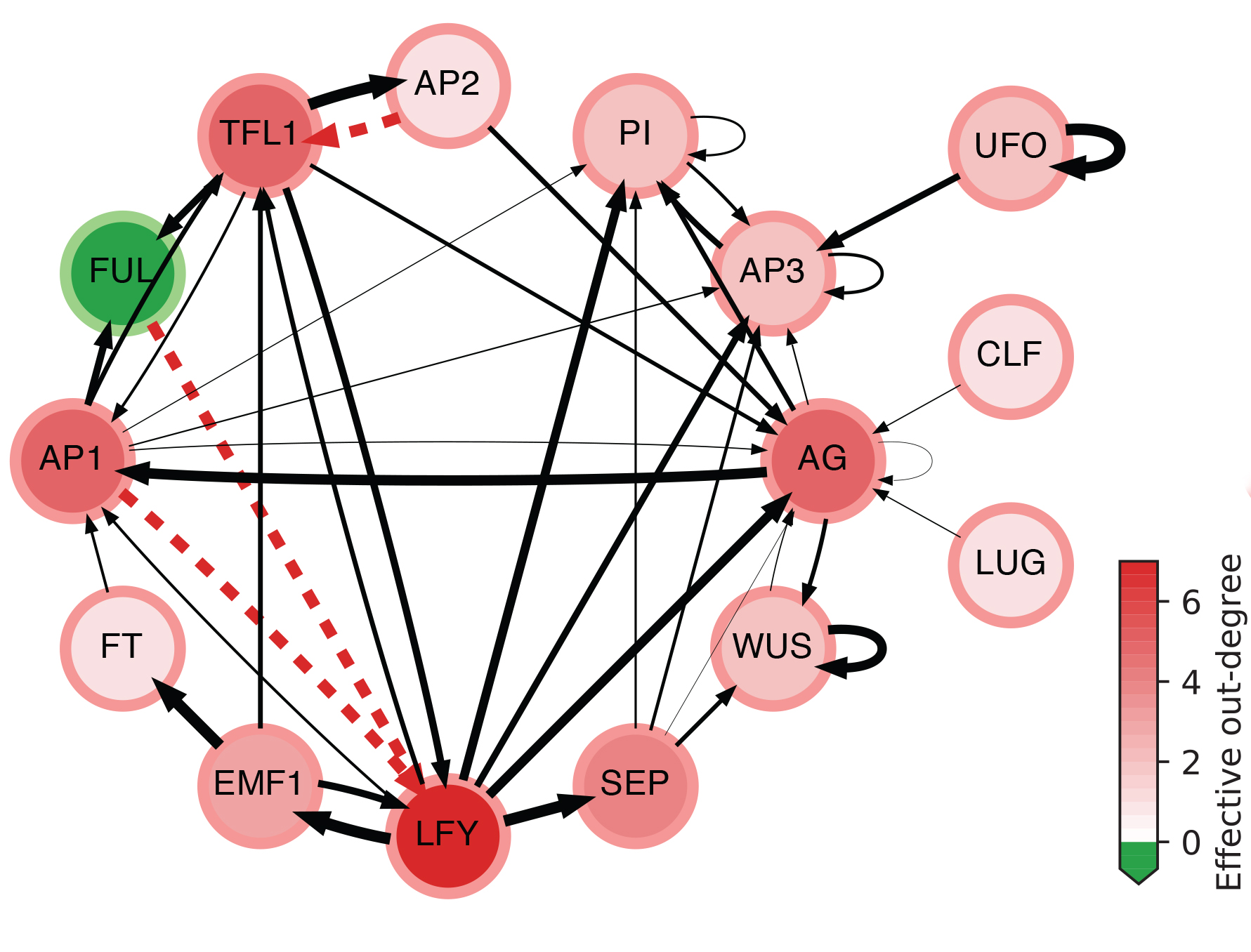
The effective graph of a Boolean Network model of gene regulation in Arabidopsis Thaliana. Edge thickness denotes effectiveness; dashed red indicates fully redundant edges; node color intensity denotes effective out-degree; and green nodes denote cases of null effective out-degree. (see details in [Gates et al, 2021])
Control from structure and dynamics of network models of biochemical regulation.
While a recent interest in linear control has lead much recent research to infer control from the structure of network interactions, we have shown that, structural controllability, minimum dominating sets and even feedback vertex set theory fail to properly characterize controllability in systems biology models of biochemical regulation, and even in small network motifs. Indeed, structure-only methods both undershoot and overshoot the number and which sets of variables actually control these models, highlighting the importance of the system dynamics in determining control [Gates and Rocha, 2016][Gates et al, 2021]. We have also shown that the logic of automata transition functions, namely how canalizing they are, plays a key role in dynamical regime and evolvability [Manicka, Marques-Pita and Rocha, 2022], as well as on controllability [Gates et al, 2021] (see more on canalization below).
Considering the possible dynamics that can unfold on specific network structure is a focus of research in our group. In addition to control, we study prediction [Kolchinsky and Rocha, 2011], modularity [Kolchinsky, Gates and Rocha, 2015, Marques-Pita and Rocha, 2013], multi-scale integration in the dynamics of complex network, such as brain networks [Kolchinsky et al 2014], and other scalable methods to study dynamics of networks [Rocha , 2022; Parmer, Rocha, & Radicchi, 2022]---for dynamics on networks see our work on distance backbones.
Redundancy and canalization in the dynamics of automata network models of biochemical regulation.
Schema redescription with two symbols is a method to eliminate redundancy in the transition tables of Boolean automata. One symbol is used to capture redundancy of individual input variables, and another to capture permutability in sets of input variables: fully characterizing the canalization present in Boolean functions [Marques-Pita and Rocha, 2011] [Marques-Pita and Rocha, 2013] (see figure). In our formulation, canalization becomes synonymous with redundancy present in the logic of automata. This results in straightforward measures to quantify canalization in an automaton (micro-level), which is in turn integrated into a highly scalable way to characterize the collective dynamics of large-scale automata networks (macro-level). This way, our approach provides a method to link micro- to macro-level dynamics---a crux of complexity. Our methodology is applicable to any complex network that can be modelled using automata, but we focus on biochemical regulation and signalling, towards a better understanding of the (decentralized) control that orchestrates cellular activity---with the ultimate goal of explaining how do cells and tissues "compute". Our group also focuses on providing open-source code so that others can test our approach [Correia, Gates, Wang, and Rocha , 2018].
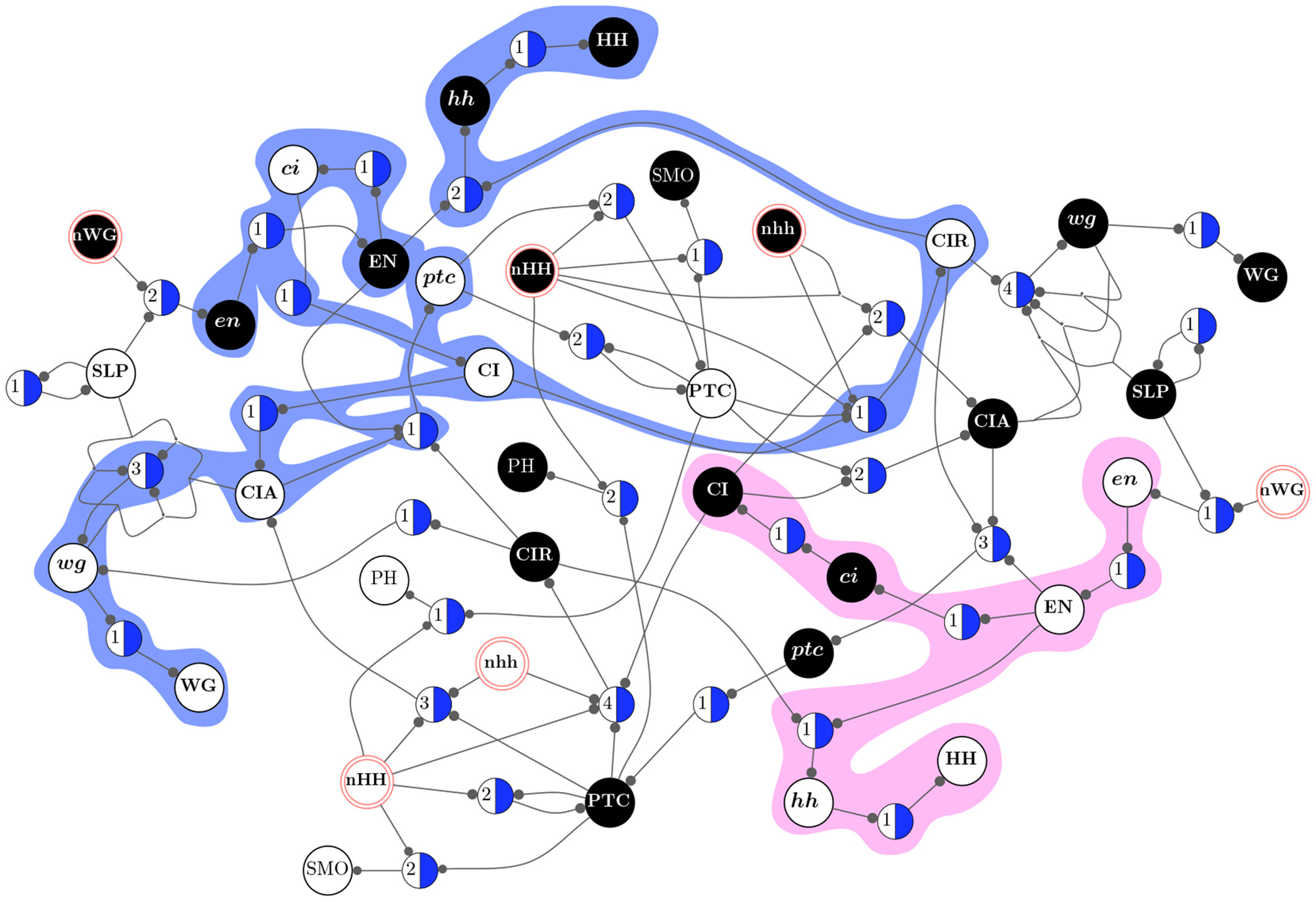
By removing redundancy (canalization) from discrete models of biochemical regulation, we can extract the effective structure that controls their dynamics, revealing their dynamical modularity (modules in the dynamics rather than in the structure of networks) and robustness [Marques-Pita and Rocha, 2013]. In particular, we can extract the minimal conditions (as schemata or motifs) and critical nodes that control convergence to attractors---associated with phenotypic behavior in these models, such as the effect of specific medications in cancer [Gates et al, 2021]. The approach is scalable because it only needs to compute the redundancy of the transition functions of each node in the network, rather than the entire dynamical landscape of the multivariate dynamical system [Rocha , 2022]. This has lead us, for instance, to obtain a better understanding of a well-known 60-variable model of the intra- and inter cellular genetic regulation of body segmentation in Drosophila Melanogaster [Marques-Pita and Rocha, 2013]. We were able to measure more accurately the size of its wild-type attractor basin (larger than previously thought), to the identify novel minimal conditions and critical nodes that control wild-type behaviour, and estimate its resilience to stochastic interventions. Similarly, we are able to characterize analytically the causal pathways in large cancer models (without estimating via Monte-Carlo simualtions) [Gates et al, 2021] and better predict the dynamical regime of large ensembles of automata networks and experimentalli-validated systems biology models [Manicka, Marques-Pita and Rocha, 2022].
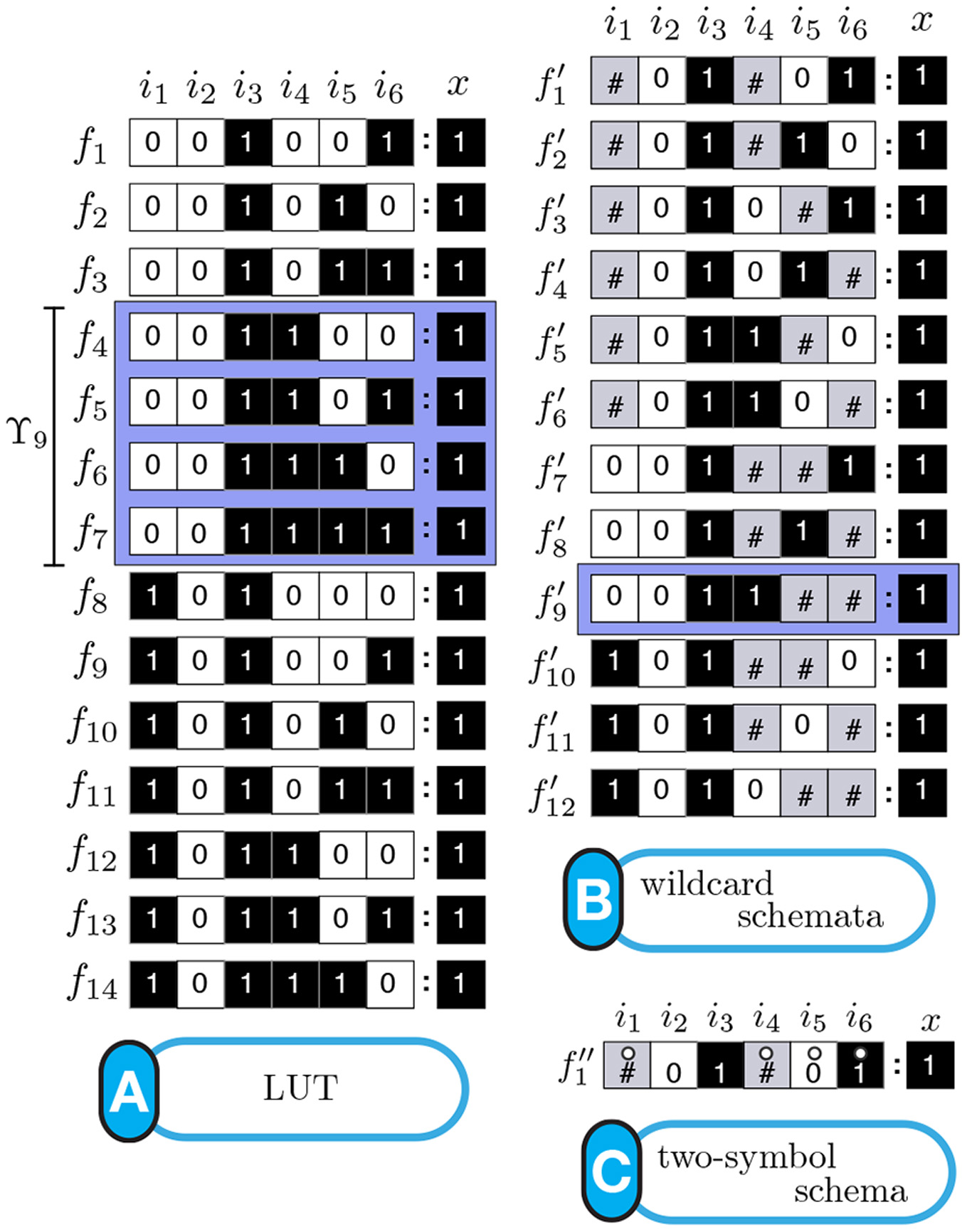
Schemata Redescription ofAutomata. (A) Look-Up table (LUT) entries of an example automaton. (B) Wildcard schema redescription; Wildcard (#) entries are redundant. (C) Two-symbol schema redescription, using the additional position-free symbol (circle); the entire set is compressed into a single schema: any inputs marked with the circle can permute. (see [Marques-Pita and Rocha, 2013] for details)
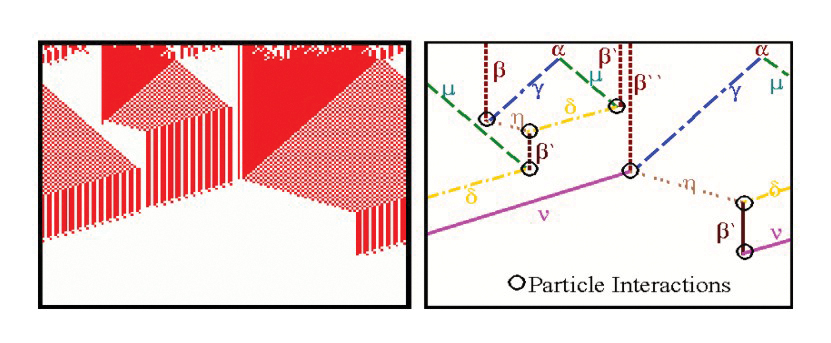
Top: Emergent Computation in the AND Rule for the CA density classification task(From Rocha and Hordijk [2005]). Bottom: two decoupled pathway modules define the dynamical collective behavior of gene regulation in a model of drosophila development (From [Marques-Pita and Rocha, 2013]).
Emergent Computation and the Origin of Representations in Evolving Cellular and Network Automata
We have been interested on the problem of how information, symbols, representations and the like can arise from a purely dynamical system of many components. This is a topic of particular interest in Cognitive Science, where the notions of representation and symbol often divide the field into opposing camps. Often, in the area of Embodied Cognition the idea of self-organization in dynamical systems leads many researchers to reject representational or semiotic elements in their models of cognition. This attitude seems not only excessive, but indeed absurd as it ignores the informational processes so important for biological organisms. Therefore, we have been working both on a re-formulation of the concept of representation for embodied cognition, as well as on simulations of dynamical systems (using Celular Automata) where one can study the origin of representations.
The Evolving Cellular Automata experiments of Crutchfield, Mitchell et al, in the late 1990’s were very exciting, as the ability of evolved cellular automata to solve non-trivial computation tasks seemed to provide clues about the origin of representations and information from dynamical systems [Mitchell, 1998] [Rocha ,1998b]. We conducted additional experiments which extended the density classification task with more difficult logical tasks [Rocha, 2000; Rocha, 2004]. Later, we proposed a re-formulation of the concept of representation in cognitive science and artificial life which is based on this work, but argues that the type of emergent computations observed in these experiments do not produce representations quite as rich as those as observed in biology and cognition [Rocha and Hordijk ,2005]. These experiments allow us to think about how to evolve symbols from artificial matter in computational environments. The figure above, depicts a space-time diagram and particle model of a CA rule evolved to solve the AND task. Some additional Figures and experiment details of CA rules for logical tasks in our experiments are also available.
We have also used our dynamical redundancy removal method to show that despite having very different collective behavior, Cellular Automata (CA) rules can be very similar at the local interaction level [Marques-Pita and Rocha, 2011]—leading us to question the tendency in complexity research to pay much more attention to emergent patterns than to local interactions. Additionally, schema redescription allows us to obtain more amenable search spaces of CA rules for the Density Classification Task—obtaining some of the best known rules for this task. [Marques-Pita and Rocha, 2008, Marques-Pita, Mitchell, and Rocha, 2008].
Additionally, by removing redundancy (canalization) from discrete automata networks, we can identify their dynamical modularity (modules in the dynamics rather than in the structure of networks.) This allows us to observe that biochemical regulation relies of pathways comprised of specific states of biochemical variables which are largely dynamically decoupled from one another and function as macroscale building blocks for collective behavior (or emergent computation) [Marques-Pita and Rocha, 2013] (see side image).
Funding Project partially funded by
- Fundacao para a Ciencia e Tecnologia, Portugal. PTDC/MEC-AND/30221/2017. Project title: “The sperm cell core genetic program: combined clinical and research approach to the diagnosis of male infertility”. 2018-2021
- National Science Foundation, Research Traineeship Program, NSF1735095: Interdisciplinary Training in Complex Networks and Systems, 2017-2022
- Fulbright U.S. Scholar grant, J. William Fulbright Foreign Scholarship Board (FFSB). 2016-2017
- Fundacao para a Ciencia e Tecnologia, Portugal. PTDC/EIA-CCO/114108/2009. Project title: “Collective Computation and Control in Complex Biochemical Systems”
- Fundação Luso-Americana para o Desenvolvimento (Portugal) and National Science Foundation (USA), 2012-2014. Project title: “Network Mining For Gene Regulation And Biochemical Signaling.” (171/11)
Project Members (Current and Former)

Luis Rocha (PI)

Reka Albert

Rion Brattig Correia

Felipe Xavier Costa

Alex Gates

Artemy Kolchinsky

Santosh Manicka

Austin Marcus

Manuel Marques Pita

Melanie Mitchell

Thomas Parmer

Filippo Radicchi

Jordan C. Rozum

Herbert Sizek

Xuan Wang
Selected Project Publications
- M. De Domenico, L. Allegri, G. Caldarelli, V. d'Andrea, B. Di Camillo, L.M. Rocha, J. Rozum, R. Sbarbati, F. Zambelli [2025]. "Challenges and opportunities for digital twins in precision medicine: a complex systems perspective." npj Digital Medicine 8, 37. DOI: 10.1038/s41746-024-01402-3. Preprint also available: arXiv:2405.09649
- A.M. Marcus, J. Rozum, H. Sizek, and L.M. Rocha. [2024]. "CANA v1. 0.0 and schematodes: efficient quantification of symmetry in Boolean automata.". arXiv:2405.07123. DOI: 10.48550/arXiv.2405.07123.
- K.H. Park, F.X. Costa, L.M. Rocha, R. Albert, J.C. Rozum [2023]. "Robustness of biomolecular networks suggests functional modules far from the edge of chaos". PRX Life. 1, 023009. DOI: 10.1103/PRXLife.1.023009. Preprint available at bioRxiv:2023.06.30.547297. DOI: 10.1101/2023.06.30.547297
- Costa, F.X.; Rozum, J.C.; Marcus, A.M.; Rocha, L.M. [2023]. "Effective Connectivity and Bias Entropy Improve Prediction of Dynamical Regime in Automata Networks". Entropy. 25(2):374. doi: 10.3390/e25020374.
- T. Parmer and L.M. Rocha. [2023]. "Dynamical Modularity in Automata Models of Biochemical Networks". arXiv:2303.16361. DOI: 10.48550/arXiv.2303.16361
- Parmer, T., Rocha, L.M. & Radicchi, F. [2022]. "Influence maximization in Boolean networks". Nature Communications. 13, 3457, DOI: 10.1038/s41467-022-31066-0.
- L.M. Rocha [2022]. "On the feasibility of dynamical analysis of network models of biochemical regulation". Bioinformatics. btac360, DOI: 10.1093/bioinformatics/btac360. PrePrint: arXiv:2110.10821.
- Manicka, S., M. Marques-Pita, and L.M. Rocha [2022]. Effective connectivity determines the critical dynamics of biochemical networks. Journal of the Royal Society Interface. 19(186):20210659. DOI: 10.1098/rsif.2021.0659.
- Gates, A., R.B. Correia, X. Wang, and L.M. Rocha [2021]. "The effective graph reveals redundancy, canalization, and control pathways in biochemical regulation and signaling". Proceedings of the National Academy of Sciences. 118 (12) e2022598118; DOI: 10.1073/pnas.2022598118.
- Gates, A., R.B. Correia, X. Wang, and L.M. Rocha [2020]. "The effective graph: a weighted graph that captures nonlinear logical redundancy in biochemical systems". Complex Networks 2020. The 9th International Workshop on Complex Networks and Their Applications. Dec. 1-3, 2020, Madrid, Spain (Online).
- A. Gates, X. Wang, R.B. Correia, L.M. Rocha [2019]. "The effective graph captures canalizing dynamics and control in Boolean network models of biochemical regulation." NetSci 2019: International School and Conference on Network Science. May 27-31, 2019, Burlington, VT, USA.
- R.B. Correia, A.J. Gates, X. Wang, L.M. Rocha [2018]. CANA: A python package for quantifying control and canalization in Boolean Networks. Frontiers in Physiology. 9: 1046. DOI: 10.3389/fphys.2018.01046
- Correia, R.B, Gates, A., Manicka, S., M. Marques-Pita, X. Wang, and L.M. Rocha [2017]. "The effective structure of complex networks: Canalization in the dynamics of complex networks drives dynamics, criticality and control". Complex Networks 2017. The 6th International Workshop on Complex Networks & Their Applications. Nov. 29 - Dec. 01, 2017, Lyon, pp. 354-355
- A. Gates and L.M. Rocha. [2016] "Control of complex networks requires both structure and dynamics." Scientific Reports 6, 24456. doi: 10.1038/srep24456.
- A. Kolchinsky, A. Gates and L.M. Rocha. [2015] "Modularity and the spread of perturbations in complex dynamical systems." Phys. Rev. E Rapid Communications. 92, 060801(R).
- A. Kolchinsky, M. P. Van Den Heuvel, A. Griffa, P. Hagmann, L.M. Rocha, O. Sporns, J. Goni [2014]. "Multi-scale Integration and Predictability in Resting State Brain Activity". Frontiers in Neuroinformatics, 8:66. doi: 10.3389/fninf.2014.00066.
- A. Gates and L.M. Rocha [2014]. “Structure and dynamics affect the controllability of complex systems: a Preliminary Study”. Artificial Life 14: Proceedings of the Fourteenth International Conference on the Synthesis and Simulation of Living Systems: 429-430, MIT Press.
- M. Marques-Pita and L.M. Rocha [2013]. “Canalization and control in automata networks: body segmentation in Drosophila Melanogaster”. PLoS ONE, 8(3): e55946. doi:10.1371/journal.pone.0055946.
- A. Kolchinsky, and L.M. Rocha [2011].”Prediction and Modularity in Dynamical Systems“.In: Advances in Artificial Life, Proceedings of the Eleventh European Conference on the Synthesis and Simulation of Living Systems (ECAL 2011). August 8 – 12, 2011, Paris, France,. MIT Press, pp. 423-430.
- M. Mourao [2011]. Reverse engineering the mechanisms and dynamical behavior of complex biochemical pathways. PhD Dissertation, Indiana University
- M. Marques-Pita and L.M. Rocha [2011]. “Schema Redescription in Cellular Automata: Revisiting Emergence in Complex Systems“. In: The 2011 IEEE Symposium on Artificial Life, at the IEEE Symposium Series on Computational Intelligence 2011. April 11 – 15, 201, Paris, France,. IEEE Press, pp: 233-240.
- M. Marques-Pita, M. Mitchell, and L.M. Rocha [2008]. “The Role of Conceptual Structure in Learning Cellular Automata to Perform Collective Computation“. In: Unconventional Computation: 7th International Conference (UC 2008). Lecture Notes in Computer Science. Springer-Verlag, 5204: 146-163.
- Rocha, Luis M. and W. Hordijk [2005]. "Material Representations: From the Genetic Code to the Evolution of Cellular Automata". Artificial Life. 11 (1-2), pp. 189 - 214
- Rocha, Luis M. [2000]. "Syntactic autonomy, cellular automata, and RNA editing: or why self-organization needs symbols to evolve and how it might evolve them". In: Closure: Emergent Organizations and Their Dynamics. Chandler J.L.R. and G, Van de Vijver (Eds.) Annals of the New York Academy of Sciences. Vol. 901, pp 207-223.