6. Von Neumann and Natural Selection

By Luis M. Rocha

Lecture notes for ISE483/SSIE583 - Evolutionary Systems and Biologically Inspired Computing. Spring 2024. Systems Science and Industrial Engineering Department, Thomas J. Watson School of Engineering and Applied Science, Binghamton University. Also available in adobe acrobat pdf format

"Turing invented the stored-program computer, and von Neumann showed that the description is separate from the universal constructor. This is not trivial. Physicist Erwin Schrödinger confused the program and the constructor in his 1944 book What is Life?, in which he saw chromosomes as “architect's plan and builder's craft in one”. This is wrong. The code script contains only a description of the executive function, not the function itself." [Brenner, 2012]

Von Neumann thought of his logical model of self-reproduction as an answer to the observation that, unlike machines, biological organisms have the ability to self-replicate while seemingly increasing their complexity without limit. Mechanical artefacts are instead produced via more complicated factories (as opposed to self-production) and can only degenerate in their complexity. He was searching for a threshold of complexity beyond which machines self-reproduce (with no outside control) while possibly increasing their complexity.

In a posthumous book edited by Arthur Burks, Von Neumann [1966] produced a Cellular Automata implementation of his theory. But the overall theory was introduced in five lectures at the University of Illinois in 1949 [Von Neumann, 1949]. Unlike what Burks' posthumous book implies (and most people take from the theory), Von Neumann was not looking to show how machines can self-reproduce. In the Illinois lectures, he states that achieving self-replication is trivial, and attainable by non-living structures like crystals which do not grow in complexity. Indeed, the goal was a logical theory of life that could explain how organisms locally beat the second law of thermodynamics: a minimum complexity threshold for evolution by natural selection. He clearly stated that the logic he reached (see Figure 1 and explanation below) is not the simplest way to achieve mere self-replication. He was instead after the logical requirements for evolvable matter via inherited variation.

Von Neumann concluded that the threshold of complexity for evolvable automata (machines) entails a memory-stored description Φ(X) that can be interpreted by a universal constructor automaton A to produce any automaton X; if a description of A, Φ(A), is fed to A itself, then a new copy of A is obtained. However, to avoid a logical paradox of self-reference, the description, which cannot describe itself, must be both copied (undecoded role) and translated (decoded role) into the described automaton. This way, in addition to the universal constructor, an automaton B capable of copying any description, Φ(X), is included in the self-replication scheme. A third automaton C is also included to perform all the manipulation of descriptions necessary—a sort of operating system. To sum it up, the self-replicating system contains the set of automata (A + B + C) and a description Φ(A + B + C); the description is fed to B which copies it three times (assuming destruction of the original); one of these copies is then fed to A which produces another automaton (A + B + C); the second copy is then handled separately to the new automaton which together with this description is also able to self-reproduce; the third copy is kept so that the self-reproducing capability may be maintained (it is also assumed that A destroys utilized descriptions). See Figure 1(i) for a visual representation.

Figure 1: Von Neumann's (threshold of complexity) scheme for evolving machines. i) The four necessary automata and their separate description. ii) A mutation to the description of automaton D' leads to offspring variation in subsequent generation.

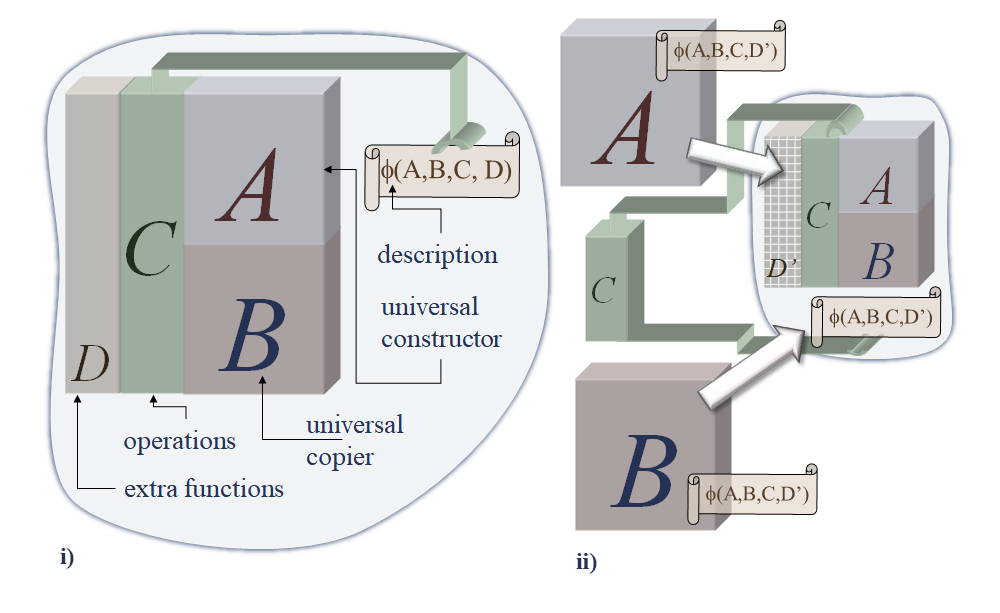
Notice that the description, or memory, is used in two different ways: it is both translated and copied. In the first role, it controls (or programs) the construction of an automaton by causing a sequence of activities in the machine—Von Neumann named it the active role of information. In the second role, the description is simply copied without reference to its meaning—the passive role of information. In other words, the decoded description controls/programs construction, and the undecoded description is copied separately, passing along its stored information (memory) to the next generation, without access to its meaning. This parallels the horizontal and vertical transmission of genetic information in biological organisms (protein translation via ribosomes and DNA duplication via polymerases, respectively), which is all the more remarkable since Von Neumann proposed this scheme before the structure of the DNA molecule was uncovered by Watson, Crick and Franklin [Watson and Crick, 1953]—though after the Avery-MacLeod-McCarty [1944] experiment which identified DNA has the carrier of genetic information.

"The concept of the gene as a symbolic representation of the organism—a code script—is a fundamental feature of the living world and must form the kernel of biological theory. ". [Brenner, 2012]

The notion of description-based self-reproduction implies a language. A description must be cast on some symbol system while it must also ultimately be implemented by some physical structure (or axiomatic/logical system if considering an exclusively formal treatment) [Rocha & Hordijk, 2005]. When A interprets a description to construct some automaton, a semantic code is utilized to map instructions into construction commands to be performed. When B copies a description, only its syntactic aspects are replicated. Now, the language of this semantic code presupposes a set of primitives (e.g. parts and processes) for which the instructions are said to "stand for". Descriptions are not universal insofar as they refer to these building blocks which cannot be changed without altering the significance of the descriptions. The building blocks ultimately produce the dynamics, behavior, and/or functionality of the overall system. In Biology, we can think of the genetic code as instantiating such a language. Genes are one-dimensional, linear descriptions that encode specific parts: amino acids chains with are constructed by folding into three-dimensional, dynamical machines [Pattee, 2022]. In a computational setting parts are typically logical operations, but they must ultimately be material building blocks (in hardware) where instructions in the language are decoded/translated to specific physical actions [Rocha & Hordijk, 2005].

Von Neumann’s active vs. passive modes of information, or the decoded vs undecoded use of genetic descriptions in biology, can also be cast as interpreted vs. uninterpreted material representations [Rocha & Hordijk, 2005], where interpretation is understood in the sense of a computer language compiler. However, the term “interpretation” can be confusing and arguably best left for when different alternative meanings for symbols arise at higher levels of organism engagement with an environment, cognition, or social interaction [Pattee, 2021]. For our purposes, what is important is the recognition of the necessity of two distinct roles for descriptions in evolvable self-replication. Per Von Neumann’s scheme, and per what we know about biology today [Brenner, 2012; Pattee, 2021, 2022]: organisms (or evolvable machines) decode descriptions to control material self-construction (horizontally), and also copy (undecoded) descriptions separately and vertically for offspring (though horizontal transmission of undecoded descriptions is also possible.)

Open-ended evolution and natural selection

"Biologists ask only three questions of a living organism: how does it work? How is it built? And how did it get that way? They are problems embodied in the classical fields of physiology, embryology and evolution. And at the core of everything are the tapes containing the descriptions to build these special Turing machines.". [Brenner, 2012]

Perhaps the most important consequence of separate descriptions in Von Neumann's self-reproduction scheme (and Turing's Tape) is its opening the possibility for open-ended evolution [Rocha, 1998; McMullin, 2000]. As Von Neumann [1966] discussed, and shown in Figure 1(ii), if the description of the self-reproducing automata is changed (mutated), in a way as to not affect the basic functioning of (A + B + C) then, the new automaton (A + B + C)` will be slightly different from its parent. Von Neumann used a new automaton D to be included in the self-replicating organism, whose function does not disturb the basic performance of (A + B + C); if there is a mutation in the D part of the description, say D`, then the system (A + B + C + D) + Φ(A + B + C + D`) will produce (A + B + C + D`) + Φ(A + B + C + D`). Von Neumann [1966, page 86] further proposed that non-trivial self-reproduction should include this "ability to undergo inheritable mutations as well as the ability to make another organism like the original", to distinguish it from "naive" self-reproduction like growing crystals.

Notice that changes in (A + B + C + D) are not heritable, only changes in the description, Φ(A + B + C + D), are inherited by the automaton's offspring and are thus relevant for evolution. This ability to transmit mutations (vertically) is precisely at the core of the principle of natural selection of modern Darwinism. Through variation (mutation) populations of different organisms are produced; the statistical bias these mutations impose on reproduction rates of organisms will create survival differentials (fitness) on the population which define natural selection. In principle, if the language of description is rich enough, an endless variety of organisms can be evolved: open-ended evolution.

The evolvability of a self-reproducing system is dependent on the parts used by the semantic code. If the parts are very simple, then the descriptions will have to be very complicated, whereas if the parts possess rich dynamic properties, the descriptions can be simpler since they will take for granted a lot of the dynamics that otherwise would have to be specified. In the genetic system, genes do not have to specify the functional characteristics of the proteins produced, but simply the string of amino acids that will produce that functionality "for free" [Moreno et al, 1994]. Furthermore, there is a trade-off between programmability and evolvability [Conrad, 1983, 1990] which grants some self-reproducing systems no evolutionary potential whatsoever. When descriptions require high programmability they will be very sensitive to damage. Low programmability grants self-reproducing systems the ability to change without destroying their own organization, though it also reduces the space of possible evolvable configurations [Rocha, 2001].

Considering a varying degree of programmability is crucial to understand the power of the Von Neumann’s theory. He demonstrated the logical feasibility of a universal constructor (A) for the self-replication system using a 29-state cellular automaton [Von Neumann, 1966]. But this specification is best seen as a specific mathematical instance of his general theory of evolvable complexity. More recently, simpler computational implementations of that mathematical proof have been reached [e.g. Pesavento, 1995, see Sipper, 1998]. But Von Neumann famously said that by pursuing implementations of his theory, that is, “by formalizing the problem” he was perhaps “throwing away the baby with the bath water.” Indeed, many people have confused the implementation for the theory, e.g. when suggesting that the overall theory is brittle, and thus not a good model for how living organisms evolve.

The original and current computer implementations are indeed brittle because they are cast in our high-programmability computer languages (e.g. cellular automata), but the qualitative theory put in terms of the A,B,C & D machines outlined above is agnostic as to how one implements it. I side with Pattee [Pattee, & Raczaszek-Leonardi, 2012] and Brenner [2012] in thinking the theory captures quite well (better than any other) what biological cells do, and those are quite robust. In principle, if one adds redundancy to a translation code (like the genetic code) and other components, one can make the artificial implementations of the system much less brittle. Many have argued that the theory should be implemented materially, not logically/computationally to achieve low-programmability and robust emergence of functionality (e.g. Moreno et al [1994], Cariani [1989, 1992]).

The A automaton implementing the decoding/translation function, like any code, is fragile to new semantic assignments. Letters are assigned specific meanings , e.g. "lion" in English or in the genetic code UAA, UAG and UGA signifying the stop codon or AUG the methionine amino acid. The semantics of any language are highly affected if those code assignments are tampered with. If by "lion" I mean "chair" English speakers will be confused–and I may even induce someone to be killed by a real lion if I instruct people to sit on them. Similarly, the genetic code is very brittle to changing ribosome/tRNA assignments such as the examples above, which is why we observe almost no variation of the genetic code on earth. However, the genetic code has built-in redundancy to lead to fewer errors in fast translation (only 20 amino acids for 64 possible codon-aminoacid assignments). This adds much robustness in decoding/translation, but not to the ultimate code assignments themselves; if those are tamped with, organisms are likely not viable. In principle, this type of redundancy can be added to artificial implementations of Von Neumann's theory as well [Conrad, 1990]. This would make those less brittle to perturbation in translation, but still as brittle as the genetic code for new code assignments. Indeed, Von Neumann's theory suggests that machines evolved accordingly would have an A automaton with a very conserved code and would only survive if there is built-in redundancy in the code assignments (for reliability under noise).

Turing and Von Neumann were the first to correctly formalize the required inheritance mechanism behind neo-Darwinian evolution by Natural Selection. This understanding of the most fundamental design principle of life, puts Turing and Von Neumann on the Parthenon of great thinkers in Biology, alongside Darwin and Mendel [Brenner, 2012]. The dovetailing of computational thinking and biology, inherent in the cybernetics movement of Turing, Von Neumann, Shannon, Wiener and others, emphasizes how (material) control of symbolic information is the hallmark of both computation and biocomplexity.

6. Von Neumann and Natural Selection

By Luis M. Rocha

Von Neumann's Theory of Evolvable Self-Reproduction

Open-ended evolution and natural selection

Further Readings and References