3. Modeling the World and Systems Approach to Life
By Luis M. Rocha
Lecture notes for ISE483/SSIE583 - Evolutionary Systems and Biologically Inspired Computing. Spring 2025. Systems Science and Industrial Engineering Department, Thomas J. Watson School of Engineering and Applied Science, Binghamton University. Also available in adobe acrobat pdf format. A companion AI-Generated podcast via Google NotebookLM is also available for fun (but it does not substitute the lecture notes at all! it brings up many connections not really in the argument, it is provided for fun only.)
"When you can measure what you are speaking of and express it in numbers you know that on which you are discoursing. But if you cannot measure it and express it in numbers. your knowledge is of a very meagre and unsatisfactory kind." Lord Kelvin

The Nature of Information and Information Processes in Nature1
The word information derives from the Latin informare (in + formare), meaning to give form, shape, or character to. Etymologically, it is therefore understood to be the formative principle of something, or to imbue with some specific character or quality. However, for hundreds of years, the word information is used to signify knowledge and aspects of cognition such as meaning, instruction, communication, representation, signs, symbols, etc. This can be clearly appreciated in the Oxford English Dictionary, which defines information as "the action of informing; formation or molding of the mind or character, training, instruction, teaching; communication of instructive knowledge".
When we look at the world and study reality, we see order and structure everywhere. There is nothing that escapes description or explanation, even in the natural sciences where phenomena appear sometimes catastrophic, chaotic and stochastic. A good example of order and information are our roads. Information can be delivered by signs. Drivers know that signs are not distant things, but they are about distant things in the road. What signs deliver are not things but a sense or knowledge of things – a message. For information to work that way, there have to be signs. These are special objects whose function is to be about other objects. The function of signs is reference rather than presence. Thus a system of signs is crucial for information to exist and be useful in a world, particularly for the world of drivers!
The central structure of information is therefore a relation among signs, objects or things, and agents capable of understanding (or decoding) the signs. An AGENT is informed by a SIGN about some THING. There are many names for the three parts of this relation. The AGENT can be thought of as the recipient of information, the listener, reader, interpretant, spectator, investigator, computer, cell, etc. The SIGN has been called the signal, symbol, vehicle, or messenger. And the about-some-THING is the message, the meaning, the content, the news, the intelligence, or the information.
The SIGN-THING-AGENT relation is often understood as a sign-system, and the discipline that studies sign systems is known as Semiotics. In addition to the triad of a sign-system, a complete understanding of information requires the definition of the relevant context: an AGENT is informed by a SIGN about some THING in a certain CONTEXT. Indeed, (Peircean) semiotics emphasizes the pragmatics of sign-systems, in addition to the more well-known dimensions of syntax and semantics. Therefore, a complete (semiotic) understanding of information studies these three dimensions of sign-systems:
- Semantics: the content or meaning of the SIGN of a THING for an AGENT; it studies all aspects of the relation between signs and objects for an agent, in other words, the study of meaning.
- Syntax: the characteristics of signs and symbols devoid of meaning; it studies all aspects of the relation among signs such as their rules of operation, production, storage, and manipulation.
- Pragmatics: the context of signs and repercussions of sign-systems in an environment; it studies how context influences the interpretation of signs and how well a signs-system represents some aspect of the environment.
Signs carry information content to be delivered to agents. However, it is also useful to understand that some signs are more easily used as referents than others. In the beginning of the 20th century, Charles Sanders Peirce defined a typology of signs:
- Icons are direct representations of objects. They are similar to the thing they represent. Examples are pictorial road signs, scale models, and of course the icons on your computer. A footprint on the sand is an icon of a foot.
- Indices are indirect representations of objects, but necessarily related. Smoke is an index of fire, the bell is an index of the tolling stroke, and a footprint is an index of a person.
- Symbols are arbitrary representations of objects, which require exclusively a social convention to be understood. A road sign with a red circle and a white background denotes something which is illegal because we have agreed on its arbitrary meaning. To emphasize the conventional aspect of the semantics of symbols, consider the example of variations in road signs: in the US yellow diamond signs denote cautionary warnings, whereas in Europe a red triangle over a white background is used for the same purpose. We can see that convention establishes a code, agreed by a group of agents, for understanding (decoding) the information contained in symbols. For instance, smoke is an index of fire, but if we agree on an appropriate code (e.g. Morse code) we can use smoke signals to communicate symbolically.
Clearly, signs may have iconic, symbolic and indexical elements. Our alphabet is completely symbolic, as the sound assigned to each letter is purely conventional. But other writing systems such as Egyptian or Mayan hieroglyphs, and some Chinese characters use a combination of phonetic symbols with icons and indices. Our road signs are also a good example of signs with symbolic (numbers, letters and conventional shapes), iconic (representations of people and animals) and indexical (crossing out bars) elements.
Finally, it is important to note that due to the arbitrary nature of convention, symbols can be manipulated without reference to content (syntactically). This feature of symbols is what enables computers to operate. As an example of symbol manipulation without recourse to content, let us re-arrange the letters of a word, say "deal": dale, adel, dela, lead, adle, etc. We can produce all possible permutations (4! = 4×3×2×1 = 24) of the word whether they have meaning or not. After manipulation, we can choose which ones have meaning (in some language), but that process is now a semantic one, whereas symbol manipulation is purely syntactic. All signs rely on a certain amount of convention, as all signs have a pragmatic (social) dimension, but symbols are the only signs which require exclusively a social convention, or code, to be understood.
We are used to think of information as pertaining purely to the human realm. In particular, the use of symbolic information, as in our writing system, is thought of as technology used exclusively by humans. Symbols, we have learned, rely on a code, or convention, between symbols and meanings. Such a conventional relation usually specifies rules created by a human community. But it can have a more general definition:
A code can be defined as a set of rules that establish a correspondence between two independent worlds. The Morse code, for example, connects certain combinations of dots and dashes with the letters of the alphabet. The Highway Code is a liaison between illustrated signals and driving behaviours. A language makes words stand for real objects of the physical World." [Barbieri, 2003, page 94]
We can thus think of a code as a process that implements correspondence rules between two independent worlds (or classes of objects), by ascribing meaning to arbitrary symbols. Therefore, meaning is not a characteristic of the individual symbols but a convention of the collection of producers and recipients of the encoded information.
Interestingly, we can see such processes in Nature, where the producers and recipients are not human. The prime example is the genetic code, which establishes a correspondence between DNA (the symbolic genes which store information) and proteins, the stuff life on Earth is built of. With very small variations, the genetic code is the same for all life forms. In this sense, we can think of the genetic system and cellular reproduction as a symbolic code whose convention is “accepted” by the collection of all life forms.
Other codes exist in Nature, such as signal transduction from the surface of cells to the genetic system, neural information processing, antigen recognition by antibodies in the immune system, etc. We can also think of animal communication mechanisms, such as the ant pheromone trails, bird signals, etc. Unlike the genetic system, however, most information processes in nature are of an analog rather than digital nature. Throughout this course we will discuss several of these natural codes.
formalizing knowledge: uncovering the design principles of nature2
Once we create symbols, we can also hypothesize relationships among the symbols which we can later check for consistency with what we really observe in the World. By creating relationships among the symbols of things we observe in the World, we are in effect formalizing our knowledge of the World. By formalizing we mean the creation of rules, such as verbal arguments and mathematical equations, which define how our symbols relate to one another. In a formalism, the rules that manipulate symbols are independent of their meaning in the sense that they can be calculated mechanically without worrying what symbols stand for.
It is interesting to note that the ability to abstract characteristics of the world from the world itself took thousands of years to be fully established. Even the concept of number, at first was not dissociated from the items being counted. Indeed, several languages (e.g. Japanese) retain vestiges of this process, as different objects are counted with different variations of names for numbers. Physics was the first science to construct precise formal rules of the things in the world. Aristotle (484-322 BC) was the first to relate symbols more explicitly to the external world and to successively clarify the nature of the symbol-world (symbol-matter) relation. “In his Physics he proposed that the two main factors which determine an object's speed are its weight and the density of the medium through which it travels. More importantly, he recognized that there could be mathematical rules which could describe the relation between an object's weight, the medium's density and the consequent rate of fall.” [Cariani, 1989, page 52] The rules he proposed to describe this relations were:
- For freely falling or freely rising bodies: speed is proportional to the density of the medium.
- In forced motion: speed is directly proportional to the force applied and inversely proportional to the mass of the body moved.
This was the first time that the relationships between observable quantities were hypothesized and used in calculations. Such a formalization of rules as a hypothesis to be tested is what a model is all about. Knowledge is built upon models such as this that sustain our observations of the World.
"While these quantities were expressed in terms of numbers, they were still generally regarded as inherent properties of the objects themselves. It was not until Galileo took the interrelationships of the signs themselves as the objects of study that we even see the beginnings of what was to be progressive dissociation of the symbols from the objects represented. Galileo's insight was that the symbols themselves and their interrelations could be studied mathematically quite apart from the relations in the objects that they represented. This process of abstraction was further extended by Newton, who saw that symbols arising from observation […] are distinct from those involved in representing the physical laws which govern the subsequent motion". [Cariani, 1989, page 52]
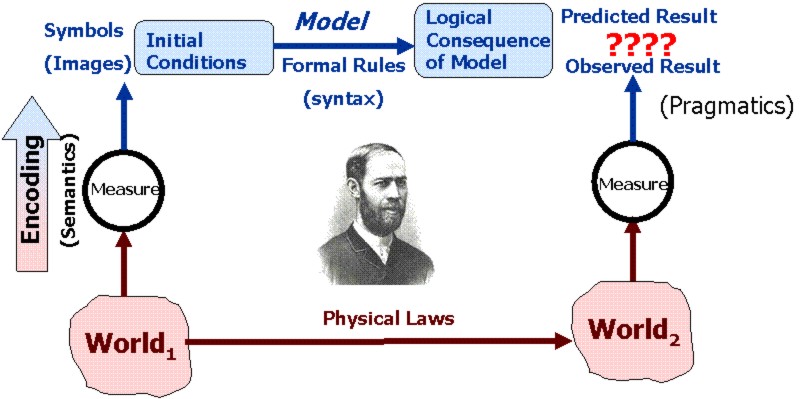
Figure 1: The Modeling Relation between knowledge and reality according to Hertz (adapted from Cariani, 1989)
"In 1894 Heinrich Hertz published his Principles of Mechanics which attempted […] to purge mechanics of metaphysical, mystical, undefined, unmeasured entities such as force and to base the theory explicitly on measurable quantities. Hertz wanted to be as clear, rigorous, and concise as possible, so that implicit, and perhaps unnecessary, concepts could be eliminated from physical theories, [which he thought should be based solely on measurable quantities]." [Cariani, 1989, page 54]. Since the results of measurements are symbols, physical theory should be about building relationships among observationally-derived symbols, that is, it should be about building formal models, which Hertz called "images":
A model is any complete and consistent set of verbal arguments, mathematical equations or computational rules which is thought to correspond to some other entity, its prototype. The prototype can be a physical, biological, social psychological or other conceptual entity.
The etymological roots of the word model lead us to the Latin word “modulus”, which refers to the act of molding, and the Latin word “modus” (a measure) which implies a change of scale in the representation of an entity. The idea of a change of scale, can be interpreted in different ways. As the prototype of a physical, social or natural object, a model represents a change on the scale of abstraction: certain particularities have been removed and simplifications are made to derive a model.
In the natural sciences, models are used as tools for dealing with reality. They are caricatures of the real system specifically build to answer questions about it. By capturing a small number of key elements and leaving out numerous details, models help us to gain a better understanding of reality and the design principles it entails. But it is still surprising how effective mathematical and computational models, these formal caricatures, can aid in the prediction of physical and social reality [Wigner, 1960].
Computational Systems Models vs Thought Experiments 3
Computation is the abstraction and automation of a formal mathematical system, or an axiomatic system. It is defined by the purely syntactic process of mapping symbols to symbols. Such mapping is the basis of the concept of mathematical function, and it is all that computers do. This abstraction requires that all the procedures to manipulate symbols are defined by unambiguous rules that do not depend on physical implementation, space, time, energy considerations or semantic interpretations given to symbols by observers. Formal computation is, by definition, implementation-independent.
Modeling, however, is not entirely a formal process. The Hertzian modeling paradigm (Figure 1) clearly relates formal, computational models to measurements of reality against which they must be validated. The measuring process transforms a physical interaction into a symbol – via a measuring device. The measuring process cannot be formalized as it ultimately depends on interacting with a specific (not implementation-independent) portion of reality. We can simulate a measurement process, but for that simulation to be a model we will need in turn to relate it to reality via another measurement, and so on indefinitely. This important aspect of modeling is often forgotten in Artificial Life, when the results of simulations are interpreted without access to real world measurements (see Chapter 2).
Likewise, a computer is a physical device that implements a particular abstract computational model as precisely as possible. Modern day computers are so successful because they can implement general-purpose computations almost independently of their specific physics. We do not have to worry about the specific physical architecture of the device as we compute, even though small errors in our computations do occur due to the physical elements of the computing device. In summary, a computation is a process of rewriting symbol strings in a formal system according to a program of rules. The following characteristics are important: (1) Operations and states are syntactic. (2) Symbols follow syntactical rules. (3) Rate of computation is irrelevant. (4)Program determines result, not speed of machine (Physical implementation is irrelevant).
Studying the design principles of life by computational means can be pursued in different ways. While we tend to refer to all of them as simulations, it is important to distinguish approaches that retain empirical validation in the natural, material World, from those that are only theoretically grounded. Only the former are based on Hertz’ modeling relation underlying the scientific method. Artifical life, based on the study of life-as-it-could-be as proposed by Langton, is circumscribed to theory (see Chapter 2). Its simulations are not scientific models in the sense of Hertz. They are in effect sophisticated computer-aided thought experiments, whose utility is the exploration of the axiomatics, corollaries, and limits of existing theories of life —computational philosophy? Another utility of such computer-aided thought experiments is the generation of bio-inspired machine learning methods, which can also be established by theoretical optimization principles. This engineering discipline does not aim to model life, but rather obtain useful methods to optimize machines and other human and social problems. Interestingly, because the utility of bio-inspired algorithms must ultimately be pragmatically decided in real-World applications, it often provides insights about and challenges to theoretical dispositions more efficiently than the computer-aided thought experiments of artificial life [Floreano & Mattiussi, 2008; Nunes de Castro, 2006].
In systems-theoretic terms, artificial life pertains to the realm of mathematical principles, where isomorphic symbol relabelings are pursued, without measurement or interpretation of experimental observations and validations in the material World [Klir, 2001; Pattee & Raczaszek-Leonardi, 2012]. It is a wholly systemhood affair, without direct access to or constraints from thinghood [Rosen, 1986]. But as Klir [2001] emphasized, the study of systemhood alone --- without thinghood interpretation or validation --- is not (complex) systems science, it is mathematics. Indeed, other systems approaches to studying life are more complete in the sense of restricting computational and systems methodologies to life-as-we-know-it, thus not getting rid of thinghood altogether. This is the case of the related fields of systems biology, computational biology, bioinformatics, and synthetic biology [Kanehisa, 2000; Kitano, 2002;Villa & Sonis, 2020; Meng & Ellis, 2020], which, like artificial life, also pursue a methodology of holistic synthesis (rather than reductionist analysis). But, unlike artificial life, these disciplines pursue the integration and synthesis of large-scale biochemical, behavioral and ecological information into complex networks and systems models that are validated via measurement of the material World, rather than exclusively from symbolic relabeling within theory.
footnotes
2This subsection is an excerpt of [Rocha and Schnell, 2005b].
3This section is indebted to many writings of Howard Pattee, including lecture notes and personal communications.
further readings and references
Aris, R. (1978). Mathematical modelling techniques. London: Pitman. (Reprinted by Dover).
Barbieri, M. [2003]. The Organic Codes: An Introduction to Semantic Biology. Cambridge University Press.
Bossel, J. (1994). Modeling and simulation. Wellesley, MA: A K Peters.
Cariani, P. (1989). On the Design of Devices with emergent Semantic Functions. PhD Dissertation, SUNY Binghamton.
Hertz, H. [1894]. Principles of Mechanics. tr. D. E. Jones and J. T. Walley. New York: Dover 1956
Kanehisa, M. [2000]. Post-genome informatics. OUP Oxford.
Kitano, H.. "Systems biology: a brief overview." Science 295.5560 [2002]: 1662-1664
Klir, G. [2001], Facets of Systems Science. Springer.
Lin, C. C. and Segel, L. A. (1974). Mathematics applied to deterministic problems in the natural sciences. New York: Macmillan Publishing. (Reprinted by SIAM).
Meng, F., & Ellis, T. [2020]. The second decade of synthetic biology: 2010–2020. Nature Communications, 11[1], 5174.
Pattee, H. H., & Raczaszek-Leonardi, J. [2012]. Laws, language and life: Howard Pattee’s classic papers on the physics of symbols with contemporary commentary [Vol. 7]. Springer Science & Business Media.
Polya, G. (1957). How to solve it: A new aspect of mathematical method. Pricenton, NJ: Princeton University Press.
Rocha, L.M. and S. Schnell (2005). “The Nature of Information”. Lecture notes for I101 – Introduction to Informatics. School of Informatics, Indiana University.
Rocha, L.M. and S. Schnell (2005b). “Modeling the World”. Lecture notes for I101 – Introduction to Informatics. School of Informatics, Indiana University.
Rosen, R. [1986], “Some Comments on Systems and System Theory”. In Int. Journal of General Systems. Vol. 13, No. 1
Saari, D. G. (2001). Chaotic elections! A mathematician looks at voting. American Mathematical Society. Also you can read: “Making sense out of consensus” by Dana MacKenzie, SIAM News. 33, (8).
Villa, A. & S.T. Sonis [2020]. "System biology." In Translational Systems Medicine and Oral Disease, pp. 9-16. Academic Press.
Wigner, E.P. [1960], "The unreasonable effectiveness of mathematics in the natural sciences". Richard courant lecture in mathematical sciences delivered at New York University, May 11, 1959. Comm. Pure Appl. Math., 13: 1-14.
for the next lectures read
Floreano, D. and C. Mattiussi [2008]. Bio-Inspired Artificial Intelligence: Theories, Methods, and Technologies. MIT Press. Available in electronic format for SUNY students. Chapter 2.
Optional: Nunes de Castro, Leandro [2006]. Fundamentals of Natural Computing: Basic Concepts, Algorithms, and Applications. Chapman & Hall. Via BU/SUNY Library. On Google Books. Chapter 2, Chapter 7, sections 7.3 – Cellular Automata Chapter 8, sections 8.1, 8.2, 8.3.10
Optional: Chapters 10, 11, 14 – Dynamics, Attractors and chaos of Flake, G. W. [1998]. The Computational Beauty of Nature: Computer Explorations of Fractals, Complex Systems, and Adaptation. MIT Press. Via BU/SUNY library..
Last Modified: February 16, 2025