Lab 4: Evolutionary Algorithms
ISE483/SSIE583: Evolutionary Systems and Biologically Inspired Computing
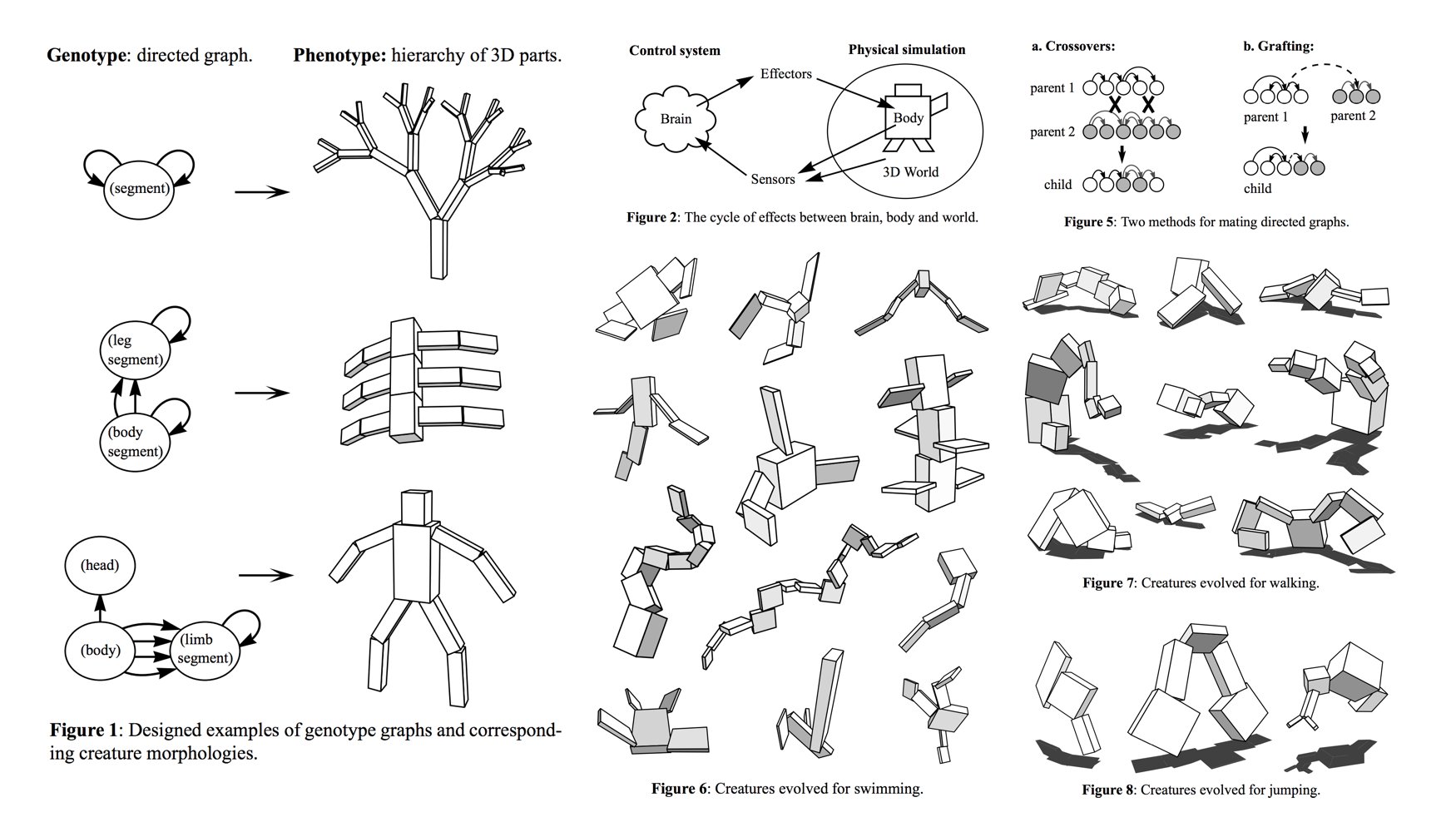
Evolved swimmers, from Karl Sim's "Evolving Virtual Creatures", SIGGRAPH '94 (source)
Assignment 4
- Chapter 1 in Floreano and Mattiussi [2008] Bio-Inspired Artificial Intelligence: Theories, Methods, and Technologies. MIT Press, provides a good introduction to evolutionary computing. Sections 1.1 to 1.10 cover 'standard genetic algorithms'.
- Please see the Lab 4 Video Presentation by Mario and Duxiao.
- Complete the following problems, worth a total of 10 points. Points for each question are shown below.
- Please submit your well-documented code as separate python files, one for each answer. Summarize your answers in a PDF document including
figures, if any. Organize this document well, clearly indicating the question being answered and the respective Python file name(s). Upload all files into the 'Assignment 4' folder in Brightspace.
- Assignment is due on April 22nd
Questions or problems? See email and office hours information.
The problems
- Genetic Algorithms.
a) [1 point] The basics of a genetic algorithm. (GA) is covered in sections 1.1 to 1.10 of the class book. A template of the implementation is available in python, containing the below functions. Describe in your own words, what each of the individual functions in a typical GA does, and how they all work in concert. For example, if you are describing the function 'evaluate' explain exactly what the function evaluates (inputs), how it evaluates (algorithm) and the range and format of the final evaluation scores (outputs). The object of this question is for you to get a picture of what's under the hood, and convey it.init()evaluate(population)
select(population, fitnesses)
recombine(father_genotype, mother_genotype, recombination_rate)
mutate(genotype, mutation_rate)
b) [1.5 points] A simple genetic algorithm. Using a population size, genome size, and number of iterations of your preference, implement a GA to evolve a 'textual' genotype in the following way. Your init() method should initialize each genotype in the population to consist of a string of random letters. The objective is to evolve genotypes that contain as many (lowercase) a's as possible. That is, you can use the number of lowercase a's present in a genotype as its fitness score in your evaluate() method. At the end of each generation, print out the best performing genotype. For solving this simple problem (by GA standards), you may choose to not use the recombine() method, but you are welcome to try it. NOTE: Your mutation method should not explicitly replace a genotype letter with 'a'. Although it will lead to solutions more quickly, it's not natural from an evolution point of view that is blind in a sense.
c) [Optional, extra 1 point] Find the global minima of the Himmelblau's function and the Holder's Table function using a binary encoding for the GA. In each case the function must respect their standard search domain, [-5,5]x[-5,5] and [-10,10]x[-10,10], respectively.
d) [2.5 points] Evolving L-systems. Implement a GA with the genotypes encoding L-system production rules similar to those that you used to generate trees in Lab 2. A good encoding scheme to use though you are welcome to use another one if you'd like is to create genotypes using only the characters in alphabet:{'F','[',']','+', '-'}that represent 'step forward', 'open branch', 'close branch', 'turn right' and 'turn left' respectively. Each genotype would represent a single production rule to replace'F'; the default axiom would be'F'(see L-System 1 specification in Q3 of Lab2, for example). Be sure to have the brackets balanced in every genotype, particularly after recombination (a paper for reference on tips for ensuring balanced brackets). You may like to have fixed-length genotypes to keep things simple, but you are welcome to play with variable-length genotypes as well. Implement the GA with roulette wheel selection with or without elite carryover. Define your own values for the recombination and mutation rates (try small values first), and most importantly formulate a good fitness function that evaluates your L-system generated at the end of a fixed number of iterations. Hints: you may want your L-system to look like a tree that is maximally banched, with branches that are maximally spread out, with as much symmetry as possible, or you may want your L-system to maximally possess the characteristics of a shape that you like, etc. By the way, it is very useful to draw your 'best-so-far' L-system at the end of every GA generation.
e) [Optional, extra 1.5 points] Increase the mutation rate and run your GA again. Does your GA find good solutions faster or slower than it did earlier? Choose at least 3 different mutation rates sufficiently spread in the range (0, 1), and discuss how mutation rate affects the search. - Discovering mathematical formulae using evolutionary software.
a) [5 points] GPlearn GPlearn is a symbolic regression tool that uses genetic programming to discover mathematical relationships among variables in a dataset. In this problem, you will use GPlearn to perform binary classification task. The dataset contains n = 16 data items representing different animal species. Each species is a data vector of 13 binary (0 or 1) variables representing features such as size, hairiness, etc. A '1' indicates the presence of that feature, and '0' otherwise. Each of the 16 species can be classified into one of two categories: bird or terrestrial animal (indicated in the dataset). GPlearn can be trained to learn the association between the species' features and their categories, and thus have it automatically compute the category using only the features. It learns associations in the form of a mathematical function, using genetic programming. The object of this problem is for you to learn to use symbolic regression as a machine learning tool.- Prepare the dataset: It should contain a set of features or variables and a binary label that indicates the class of each data point. Each feature should be represented as a binary value (0 or 1).
- Define the target function: Specify the label as the target variable and set it as a function of the input features.
- Specify search parameters: Set the search parameters for gplearn, such as the maximum number of generations, population size, and the mutation rate.
- Evaluate the results: Evaluate the discovered formulae using metrics such as accuracy, precision, recall, and F1-score. You can also visualize the results using a confusion matrix and ROC curve.
- Refine the search: If the results are not satisfactory, you can refine the search by changing the search parameters, adding or removing features, or modifying the target function.
- Test the model: Use the discovered formulae to predict the class of new data points and evaluate the performance of the model on a test dataset
Deploy the model: Once you are satisfied with the performance of the model, you can deploy it for binary classification tasks.
b) [Optional, extra 1.5 points] Summarize all your findings, by describing the length of the best formulae you found, their respective errors in fitting the data etc. You may have found different kinds of formulae, some containing simple predictors, and others with compund predictors. As a budding scientist, comment on the existence of such multiple relationships in a dataset. To make predictions about new data items that the present dataset does not contain (say, a lizard), what formula would you prefer? Would you use a longer formula that fits the present data very well? Or would you rather prefer a shorter formula that contains some error? See the 'Error vs. Complexity' plot in the bottom right of the 'Results' tab to visualize this trade-off. Do you think that this trade-off might affect how well the corresponding formulae generalize to species not available in the training dataset?
Acknowledgements
- Lab prepared by Mario Franco, Duxiao Hao, Samer Abubaker and Jack Felag, updated from original design by Artemy Kolchinsky and Santosh Manicka.
Last Modified:Apri 8, 2024