Citation: Rocha, Luis M. [2001]."Identification of Interests, Trends and Dynamics in Document Networks". Los Alamos National Laboratory LDRD ER Research Proposal. Awarded for FY02-04.
Also available in Adobe Acrobat (.pdf) format.
Abstract.
This proposal aims to investigate the hypothesis that the metric behavior of the distance functions defining these associative networks, can be used as an indicator of the relevance of collections of documents, the interests of users who have selected certain sets of documents, the trends in communities associated with sets of documents, as well the dynamics of such networks in general. The hypothesis itself is based on empirical evidence gathered and discussed in the proposal. We are requesting funds to gather more empirical evidence, investigate adequate formalisms, validate the hypothesis, and build a recommendation system that makes use of results obtained.
The success of this research would have a strong impact on information retrieval and knowledge management. If the hypothesis is correct, we would be able to predict trends in a given community by the automatic analysis of the documents they produce . We would also gain another technique to identify the relevance of documents and the interests of users, which would need to be compared to existing methodology. This impact would be felt on LANL’s current knowledge management initiatives, as well as externally, on advancing the study of DN in particular and social networks in general, as well as by producing better recommendation systems for the World Wide Web and digital libraries.
For each DN we can identify several distinct relations among documents and between documents and semantic tags used to classify documents appropriately. For instance, documents in the WWW are related via a hyperlink network, while documents in bibliographic databases are related by citation and collaboration networks [Newman, 2000]. Furthermore, documents can be related to semantic tags such as keywords used to describe their content. Although all the technology and the hypothesis here discussed would apply equally to any of these relations extracted from DN, let us exemplify the problem with the datasets we have created for the Active Recommendation Project (ARP) (http://arp.lanl.gov), part of the Library Without Walls Project, at the Research Library of the Los Alamos National Laboratory [Rocha and Bollen, 2000].
Frequency |
Keyword |
187705 |
Cell |
150795 |
studi |
149594 |
system |
140738 |
express |
127350 |
protein |
124094 |
model |
120215 |
activ |
113740 |
human |
112737 |
rat |
112702 |
patient |
To discern closeness between keywords according to the documents they classify, we compute the Keyword Semantic Proximity (KSP), obtained from A by the following formula:
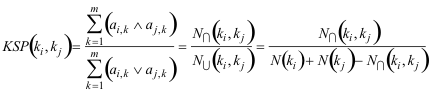
|
cell |
studi |
system |
express |
protein |
model |
activ |
human |
rat |
patient |
cell |
1.000 |
0.022 |
0.019 |
0.158 |
0.084 |
0.017 |
0.085 |
0.114 |
0.068 |
0.032 |
studi |
0.022 |
1.000 |
0.029 |
0.013 |
0.017 |
0.028 |
0.020 |
0.020 |
0.020 |
0.037 |
system |
0.019 |
0.029 |
1.000 |
0.020 |
0.017 |
0.046 |
0.022 |
0.014 |
0.021 |
0.014 |
express |
0.158 |
0.013 |
0.020 |
1.000 |
0.126 |
0.011 |
0.071 |
0.103 |
0.078 |
0.020 |
protein |
0.084 |
0.017 |
0.017 |
0.126 |
1.000 |
0.013 |
0.070 |
0.061 |
0.041 |
0.014 |
model |
0.017 |
0.028 |
0.046 |
0.011 |
0.013 |
1.000 |
0.016 |
0.016 |
0.026 |
0.005 |
activ |
0.085 |
0.020 |
0.022 |
0.071 |
0.070 |
0.016 |
1.000 |
0.058 |
0.053 |
0.021 |
human |
0.114 |
0.020 |
0.014 |
0.103 |
0.061 |
0.016 |
0.058 |
1.000 |
0.029 |
0.021 |
rat |
0.068 |
0.020 |
0.021 |
0.078 |
0.041 |
0.026 |
0.053 |
0.029 |
1.000 |
0.008 |
patient |
0.032 |
0.037 |
0.014 |
0.020 |
0.014 |
0.005 |
0.021 |
0.021 |
0.008 |
1.000 |
From the inverse of KSP we obtain a distance function between keywords:
d is a distance function because it is a nonnegative, symmetric real-valued function such that d(k, k) = 0 [Shore and Sawyer, 1993]. This distance function indicates how far, semantically, a keyword is from another in the set of keywords. This way, it defines a weighted graph D whose nodes are all of the keywords extracted from a given DN, and the edges are the values of d. Clearly, many other types of distance functions can be defined on the elements of a DN. All of the observations and hypothesis below would apply equally, but naturally, the conclusions drawn cannot be separated by how well, and how appropriately for a given application, a distance function is capable of discerning the elements of the set it is applied to. Thus, different distance functions applied to citation structures or collaboration networks, will require distinct semantic considerations than those used for keyword sets.
d (eq. 2) is not an Euclidean metric because it may violate the triangle inequality: d(k1, k2) ≤ d(k1, k3) + d(k3, k2) for some keyword k3. This means that the shortest distance between two keywords may not be the direct link but rather an indirect pathway. Such measures of distance are referred to as semi-metrics [Galvin and Shore, 1991]. Indeed, given that most social and knowledge-derived networks possess Small-World behavior [Watts, 1999], we expect that nodes which tend to be clustered in a local neighborhood of related nodes, have large distances to nodes in other clusters, but because of the existence of “gateway” nodes relating nodes in different clusters (the small-world phenomenon), smaller indirect distances between nodes in distinct clusters, through these “gateway” nodes, are to be expected.
Most hypotheses are born out of anecdotal, often personal, evidence. The one put forward here is no exception. It arose from questioning what could one infer from the semi-metric behavior of the distance functions calculated from DN. Given a distance function, what can we say about a pair of highly semi-metric elements from a finite set? And what can we say about the set, from the pairs of highly semi-metric pairs it contains?
To construct an intuition to answer these questions, one needs to deal with very familiar examples. In this case, the author could think of no DN more familiar than the set of books cited by his own dissertation [Rocha, 1997]! A database similar (but much smaller) to the one used by ARP contains the relevant information. This database contains about 150 books, each indexed by the respective Library of Congress Keywords, for example:
Kearfott, R. Baker and Vladik Kreinovich (Editors). [1996]. Applications of Interval Computations. Kluwer. Keywords: Optimization algorithms, Fuzzy logic, Uncertainty, Mathematics, Reliable Computation, Interval Computation.
|
Adaptive Systems |
Evolution |
Modeling systems |
Complex Systems |
Social Systems |
Adaptive Systems |
0.00 |
3.89 |
12.00 |
10.33 |
16.00 |
Evolution |
3.89 |
0.00 |
21.50 |
4.22 |
35.00 |
Modeling Systems |
12.00 |
21.50 |
0.00 |
5.75 |
10.00 |
Complex Systems |
10.33 |
4.22 |
5.75 |
0.00 |
19.00 |
Social Systems |
16.00 |
35.00 |
10.00 |
19.00 |
0.00 |
From this database, 86 keywords are extracted. A distance function d is calculated according to eq. 2. Table III shows the values of d for 5 of the keywords. One needs to note that this distance function is obtained from the relations extracted from a particular set of documents (in this case 150 books). Therefore, one should not expect these values to represent a universally accepted thesaurus or the associations one would anticipate from common sense knowledge. Indeed, this kind of distance is used to characterize particular information resources and users from the documents they contain or retrieve [Rocha, 2001]. In this case, the associative distances between keywords denote the way the dissertation set of books is related.
|
Adaptive Systems |
Evolution |
Modeling systems |
Complex Systems |
Social Systems |
Adaptive Systems |
0.00 |
3.89 |
12.00 |
8.11 |
16.00 |
Evolution |
3.89 |
0.00 |
9.97 |
4.22 |
19.89 |
Modeling Systems |
12.00 |
9.97 |
0.00 |
5.75 |
10.00 |
Complex Systems |
8.11 |
4.22 |
5.75 |
0.00 |
15.75 |
Social Systems |
16.00 |
19.89 |
10.00 |
15.75 |
0.00 |
Clearly, semi-metric behavior is a question of degree. For some pairs of keywords, the indirect distance provides a much shorter short-cut, a larger reduction of distance, than for others. One way to capture this property of pairs of semi-metric keywords is to compute a semi-metric ratio:
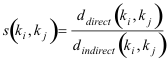
s is positive and ≥ 1 for semi-metric pairs. In our example, s(Modeling Systems,Evolution) = 21.5/9.97 =2.157. This ratio is important to discover semi-metric behavior necessary for our hypothesis as discussed below, but given that larger graphs tend to show a much larger spread of distance, s tends to increase with the number of keywords. Therefore, to be able to compare semi-metric behavior between different DN and their respective different sets of keywords, a relative semi-metric ratio is also used:
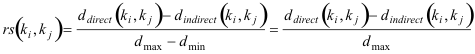
rs compares the semi-metric distance reduction to the maximum possible distance reduction in graph D. dmax is the largest distance in the graph, and dmin = 0 is the shortest distance.
Often, the direct distance between two keywords is ∞ because they do not index any documents in common. As a result, in closed graphs, s and rs are also ∞ for these cases. Thus, s and rs are not capable of discerning the degree of semi-metric behavior for pairs that do not have a finite direct distance. To detect relevant instances of this infinite semi-metric reduction, we define the below average ratio:
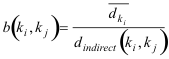
where
![]() represents the average direct distance from ki to all kj such that ddirect(k\i, kj) ≥ 0. b measures how much an
indirect distance falls below the average distance of all keywords directly associated with a keyword. Of course, b can
also be applied to pairs with finite semi-metric reduction.
represents the average direct distance from ki to all kj such that ddirect(k\i, kj) ≥ 0. b measures how much an
indirect distance falls below the average distance of all keywords directly associated with a keyword. Of course, b can
also be applied to pairs with finite semi-metric reduction.
The semi-metric ratios were applied to graph D of the dissertation database, and the semi-metric pairs with higher ratios were identified. Table V lists the top 5 pairs for semi-metric ratio s. If we rank pairs for the relative semi-metric ratio rs, there is a slight ordering of the top as the pair Evolution-DNA drops to rank 11 and the pair Life-Cognition to 6th, while the pair Evolution-Control rises to rank 3 (from 6th) and the pair Evolution-Information Theory rises to 5th (from 20th).
What is most interesting about these results is that these pairs denote the original contributions that were offered by the dissertation! Indeed, the dissertation was about using ideas and methodologies from Complex Adaptive Systems, Evolutionary Systems, and Artificial Life and apply them to Artificial Intelligence and Cognitive Science. In particular, the mathematical models (from Psychology) of cognitive categories were expanded using evolutionary ideas, by drawing an analogy with the symbolic characteristics of DNA. Furthermore, this framework was named Evolutionary Constructivism, a term that did not exist previously, but draws both from Evolutionary Theory and the Philosophy of Constructivism in Cognitive Science and Systems Theory.
To understand these results, we need to remember that the distance function d is derived from the finite set of books used in the dissertation. A high degree of semi-metricity for a keyword pair means that very few of the books in the database are simultaneously indexed by these two keywords, but that there exists a strong indirect association between these keywords via some indirect path whose short distances require the existence of many related books for each keywords pair in the pathway. Thus, a keyword pair with high semi-metric behavior, implies an association that is a property of the specific collection of documents, but not one identifiable in many included documents, and rather constructed from an indirect series of strongly related documents. In other words, the highly semi-metric pairs represent associations that “were begging to be made, given this specific collection of documents. Indeed, the two pairs (Evolution-Control and Evolution-Information Theory) ranked in the top 5 for the relative semi-metric ratio, identify two associations that are certainly implied by the collection of books (given its large subsets of Cybernetics and Information Theory books), but which were not dealt with in this dissertation – offering some topics for other dissertations!
The below average ratio b, was also used to identify keyword pairs with infinite semi-metric reduction. Those are the pairs that do not index simultaneously a single book in the collection, but which are nonetheless indirectly strongly related. For this particular dataset, the pairs with highest values of b, did not seem to produce meaningful results. This could be because, being a small, tight collection of books, the relevant associations implied by the collections are already made at least by a small set of books producing a large, but finite, distance. Such situation is not expected to occur in larger, multi-authored collections unlike the dissertation one.
The anecdotal analysis of the author’s dissertation database served the purpose of creating an intuition of what semi-metric behavior may mean for DN, but to even build a hypothesis, other more “subject-independent” datasets need to be studied.
The same semi-metric behavior ratios were used to study the ARP dataset describe above. The distance function d (eq. 2) was calculated for the set of the 500 most common keywords, and the semi-metric ratios (formulas 3 to 5) were calculated for all keyword pairs. Table VI shows the top 5 keyword pairs ranked by highest values of s.
To analyze these results, again, one must remember the original collection of documents, in this case, all the scientific articles published in journals indexed by ISI in SciSearch between the years of 1996 to 1999. A keyword pair with high semi-metricity, implies that while very few articles discuss the two topics together, a very large series of articles exists which creates an indirect pathway between these two keywords in D. To obtain a large semi-metric ratio, it is necessary that each link in the indirect pathway be defined by short distances, which in turn require the existence of many articles associated to both keywords in the link. Thus, a highly semi-metric keyword association implies that very few documents make that association, but that there are large sets of documents indirectly supporting it. In this sense, the existence of such support (particularly in scientific databases) may identify a trend that can be expected to be picked up.
The hypothesis generated from the anecdotal evidence described above, is that high semi-metric keyword associations, discovered in the distance function of DN defined by eq. 2, can (1) capture the interests of a person associated with a given small collection of documents, and (2) be used to identify trends in large, multi-authored document collections.
Clearly, much more evidence is needed to support this hypothesis. We have already applied this study to other cases such as random distance graphs (very small relative semi-metric ratios), distance graphs built from word association norms used in psychological tests (very little semi-metric behavior), distance graphs built from web-site collective usage [Bollen et al, 1999] (similar results to section 5), etc. In addition to a more thorough analysis of the semi-metric behavior of different distance functions applied to different DN, we propose to study this hypothesis by (1) creating an experimental database interface to evaluate how well the interests of users are captured by semi-metricity, and (2) studying the trend dynamics in large collections of documents such as the ARP database.
LANL’s research library is currently offering an ideal system to study how well semi-metric keyword associations capture the interests of a single person. The MyLibrary web portal (http://mylibrary.lanl.gov) allows LANL users to store links to publications in LANL’s several digital libraries with scientific articles, as well as links elsewhere on the WWW. We obtained permission from the research library to develop a recommendation system [Rocha, 2001] to be added to MyLibrary.
We propose to issue recommendations to users of MyLibrary from pairs of highly semi-metric keywords. We will use the distance function defined by eq. 2 on the keywords extracted from the documents stored by each user of the MyLibrary system. Recommendations will be issued in the form of documents that users may be unaware of but which directly associate the semi-metric keyword pairs, and directly as keywords. We will collect data from user behavior to validate how useful the recommendations are, thus gathering evidence for the first aspect of the semi-metric hypothesis.
If high semi-metricity is indeed an indicator of trends, then, by analyzing how semi-metric behavior changes in time in a DN we should be able to distinguish real trends from indirect associations never picked up by authors of documents. As a trend develops in time, we can expect the semi-metric ratios to lower, as more and more documents are added which directly associate the previously highly semi-metric keyword pairs. For instance, if the high semi-metricity pairs of Bioinformatics keywords related to Gene Expression Arrays identified in 6 do indeed imply a trend phenomenon, we should expect to see lower values of semi-metricity for these concepts in those articles published in 2000 and beyond.
Thus, we propose to collect the SciSearch articles for years 2000 and beyond, and use them as a validation set for the trends picked in the ARP database. We will also conduct the semi-metric analysis year by year, rather than the whole interval from 1996 to 1999, as well as for much more than the top 500 most frequent keywords. A more detailed study such as this, will allow us to capture the change in semi-metric behavior of a large set of keywords through the years, thus gathering evidence for the second aspect of the semi-metric hypothesis to study the dynamics of trends in DN.
We intend to tackle this proposal with the following chronological milestones:
In the first year we expect to finalize 1 and 2, and start 3 which will be ongoing through the duration of the project. In the second year we will tackle 4, 5, and 6. In the third year we will continue 6, and complete 7 and 8.
Bollen, J., H. Vandesompel, L.M. Rocha [1999]."Mining associative relations from website logs and their application to contex-dependent retrieval using Spreading Activation." In: Workshop on Organizing Web Space (WOWS), ACM Digital Libraries 99, August 1999, Berkeley, California.
Galvin, F. and S.D. Shore [1991]."Distance functions and topologies." The American Mathematical Monthly. Vol. 98, No. 7, pp. 620-623.
Klir, G.J. and B. Yuan [1995]. Fuzzy Sets and Fuzzy Logic: Theory and Applications. Prentice Hall.
Miyamoto, S. [1990]. Fuzzy Sets in Information Retrieval and Cluster Analysis. Kluwer.
Newman, MJ [2000]."The structure of scientific collaboration networks." Proc.Nat.Acad.Sci. No. 98, pp. 404-409.
Rocha, Luis M. [1997]. Evidence Sets and Contextual Genetic Algorithms: Exploring Uncertainty, Context and Embodiment in Cognitive and biological Systems. PhD. Dissertation. State University of New York at Binghamton. UMI Microform 9734528. (http://www.c3.lanl.gov/~rocha/dissert.html)
Rocha, Luis M. [2001]."TalkMine: A Soft Computing Approach to Adaptive Knowledge Recommendation." In: Soft Computing Agents: New Trends for Designing Autonomous Systems. V. Loia and S. Sessa (Eds.). Springer-Verlag. In press. (http://www.c3.lanl.gov/~rocha/softrec.html)
Rocha, Luis M. and Johan Bollen [2000]."Biologically motivated distributed designs for adaptive knowledge management." In: Design Principles for the Immune System and Other Distributed Autonomous Systems. Cohen I. And L. Segel (Eds.). Santa Fe Institute Series in the Sciences of Complexity. Oxford University Press. In Press. (http://www.c3.lanl.gov/~rocha/SFI99.html)
Shore, SD, Sawyer LJ [1993]."Explicit Metrization." Annals of the New York Academy of Sciences. v. 704 pp. 328-336 1993.
Watts, D. [1999]. Small Worlds: The Dynamics of Networks between Order and Randomness. Princeton University Press.