From Artificial Life to Semiotic Agent Models: Review and Research Directions
Table of Contents.
The term agent is used today to mean anything between a mere subroutine to a conscious entity.
There are "helper" agents for web retrieval and computer maintenance, robotic agents to venture into
inhospitable environments, agents in an economy, etc. Intuitively, for an object to be referred to as
an agent it must possess some degree of autonomy, that is, it must be in some sense distinguishable
from its environment by some kind of spatial, temporal, or functional boundary. It must possess some
kind of identity to be identifiable in its environment. To make the definition of agent useful, we often
further require that agents must have some autonomy of action, that they can engage in tasks in an
environment without direct external control. This leads us to an important definition of an agent from
the XIII century, due to Thomas Aquinas: an entity capable of election, or choice.
This is a very important definition indeed; for an entity to be referred to as an agent, it must be able
to step out of the dynamics of an environment, and make a decision about what action to take next
- a decision that may even go against the natural course of its environment. Since choice is a term
loaded with many connotations from theology, philosophy, cognitive science, and so forth, I prefer
to discuss instead the ability of some agents to step out of the dynamics of its interaction with an
environment and explore different behavior alternatives. In physics we refer to such a process as
dynamical incoherence [Pattee, 1993]. In computer science, Von Neumann, based on the work of
Turing on universal computing devices, referred to these systems as memory-based systems. That is,
systems capable of engaging with their environments beyond concurrent state-determined interaction
by using memory to store descriptions and representations of their environments. Such agents are
dynamically incoherent in the sense that their next state or action is not solely dependent on the
previous state, but also on some (random-access) stable memory that keeps the same value until it
is accessed and does not change with the dynamics of the environment-agent interaction. In contrast,
state-determined systems are dynamically coherent (or coupled) to their environments because they
function by reaction to present input and state using some iterative mapping in a state space.
Let us then refer to the view of agency as a dynamically incoherent system-environment engagement
or coupling as the strong sense of agency, and to the view of agency as some degree of identity and
autonomy in dynamically coherent system-environment coupling as the weak sense of agency. The
strong sense of agency is more precise because of its explicit requirement for memory and ability to
effectively explore and select alternatives. Indeed, the weak sense of agency is much more subjective
since the definition of autonomy, a boundary, or identity (in a loop) are largely arbitrary in
dynamically coherent couplings. Since we are interested in simulations of decision-making agents, we
need to look in more detail to agent based models with increasing levels of dynamical incoherency
with their environments.
To summarize:
- Dynamically Coherent Agents
- Rely on subjective (spacial, functional, temporal) definition of autonomy. Function
by reaction and are dynamically coupled to environments.
- Example: situated robots (wall-following machines), state-determined automata.
- Dynamically Incoherent Agents
- Possess models, syntax, language, decision-making ability. In addition to a level of
dynamical coherence with their environments (material coupling), they possess an
element of dynamical incoherence implemented by stable memory banks.
- Example: anything with symbolic memories and codes.
John Holland [1995] defines agents as rule-based input-output elements whose rules can adapt to an
environment. These rules define the behavior strategy utilized by agents to cope with a changing
environment. He also defines 7 basics or characteristics of agents and multi-agent sysems which
further specify the rule-based adaptive behavior of agents:
- Aggregation (Property) has 2 senses
- Categorization (agent level): Agents cope with their environments by grouping
things with shared characteristics and ignoring the differences.
- Emergence of large-scale behavior (multi-agent level): From the aggregation of
the behavior of individual agents (e.g. Ants in an ant colony) we observe
behavioral patterns of organization at the collective level. This leads to hierarchical
organization.
- Tagging (Mechanism). Agents need to be individualized. They possess some identity. This
in turn facilitates selection, specialization of tasks, and cooperation as different specific
roles and strategies may be defined.
- Nonlinearity (Property). The integration or aggregation of agents in multi-agent systems
is most often non-linear, in the sense that the resulting behavior cannot be linearly
decomposed into the behavior of individual agents. This also implies that multi-agent
systems lead to network causality, as effect and cause of agent behavior follow circular
loops that cannot be linearly decomposed into traditional cause and effect chains.
- Flows (Property). Multi-agent systems rely on many connections between agents that
instantiate the flow and transfer of interactions, information, materials, etc. Typically, the
network of flows is represented with graphs.
- Diversity (Property). Typically, multi-agent systems are heterogeneous, as there exist
different agent roles and behaviors. This makes the tagging mechanisms important so that
these different roles and behaviors may be identified.
- Internal Models (Mechanism) organize the rules that produce agent behavior and can be
used to let agents anticipate expected inputs from the environment. We can divide models
in 2 types.
- Implicit: Prescribes a current action under implicit prediction. This is associated
with hard-wired rules of behavior (e.g. by natural selection) and implemented by
state-determined automata. This kind of model instantiates agents which are
dynamically coupled to their environments, e.g. reactive, situated robots.
- Explicit: Use Representations stored in stable (or random access) memory to look
ahead by exploring possible alternatives. This type of model produces agents with
a level of dynamical incoherence with their environments, since they act not only
based on current state and input but also by integrating information stored in
memory. This integration can be pursued with more or less complicated reasoning
procedures. Since agents with explicit models possess behavior alternatives, we
can use them to study decision processes.
- Building blocks (Mechanism). Agents are built with less complicated components. This
allows for the instantiation of coded construction, which is essential for the recombination
of components to produce new agent with different behavior and models. Natural
selection, for instance, acts on the ability to randomly vary descriptions of agents, which
are cast on a language coding for building blocks leading to the production of new agents.
Holland's 7 basics lend themselves to our notions of dynamical incoherence, and therefore we can
well use them to describe agents and (complex adaptive) multi-agent systems.
The agents in the models described in this section are based on game-theoretic strategies, using simple
memory architectures. The environments in these models are defined exclusively by other agents,
therefore there is really no level of dynamical coupling between agent and environment. Rather, these
models aim to study only decision strategies and the evolution of strategies in an environment of other
changing strategies. However, the strategies pursued by these agents rely on present state and a
memory of only a small number of previous states and encounters. In addition, typically, the agent-rule updating is synchronous (all agents updated at the same time) and there is a determined behavior
outcome. This results in dynamically coherent multi-agent systems, since agents cannot choose when
and whether to participate, and their rules are determined by a short list of previous states.
Idealized model for real-world phenomena such as arm-races (Axelrod, 1984) and Evolutionary
Biology (Maynard-Smith, 1982), iut of Game Theory as defined by Von Neumann, Economics, and
Political Science. The dilemma is defined as follows: 2 individuals are arrested for committing a
crime together are held in separate cells; no communication is allowed; both are offered the same deal
to testify against the other (both know this); if one testifies (defects) gets a suspended sentence (S)
and the other gets the total sentence (T); if both testify (defect), the testimony is discredited: both
receive a heavy sentence (H); if neither one confesses (cooperate) both are convicted to a lesser
sentence (L). These values must obey the following 2 conditions: (1) S>L>H>T and (2) 2L>S+T.
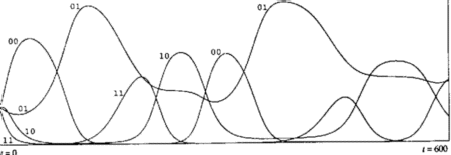
- Evolutionary Phenomena in Simple Dynamics, Kristian Lindgren [1991]. Finite
memory strategies for the iterated prisoner's dilemma (IPD) were encoded in a genetic
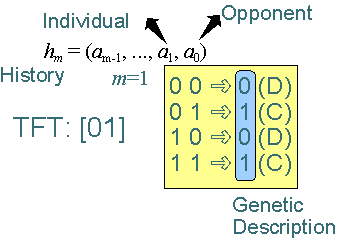
algorithm (GA). Each agent contains a strategy hm, which specifies how the agent should
play each iteration of the prisoner's dilemma game, based on a memory of size m. a0
denotes what the opponent did in the last encounter, a1 denotes what the agent did in the
last encounter, a2, what the opponent did in the one but the last encounter, and so forth.
The tit for tat (1) (TFT) strategy is a strategy of memory m=0, as it only requires memory of
what the opponent did last.
- Details of the GA:
- Encoding (see figure below). After ordering the binary possibilities of the rule,
only the right side of the rules is encoded as a genetic description. For
TFT, the binary possibilities are: 0 or 1 (opponent defected or cooperated)
and the rule specifies 0 or 1 respectively as a strategy. This way, TFT is
encoded as [01]. See figure below for an example of an extension of TFT for
m=1.
- The initial population of the GA possesses equal fractions of 4 strategies m=0: [00], [01], [10], and [11]
- Random operators. Point mutations, which flip a bit on the strategy: [01]
[00] (2x10-5); gene duplications which increase the memory size by 1
(do not change actual strategy): [01] [0101] (10-5); and split mutations,
which decrease the memory size by 1 producing two possibly distinct
strategies: [1001] [10] or [01] (10-5).
- Probability of mistake p. Probability that rule will produce opposite
outcome.
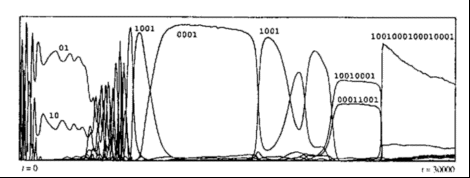
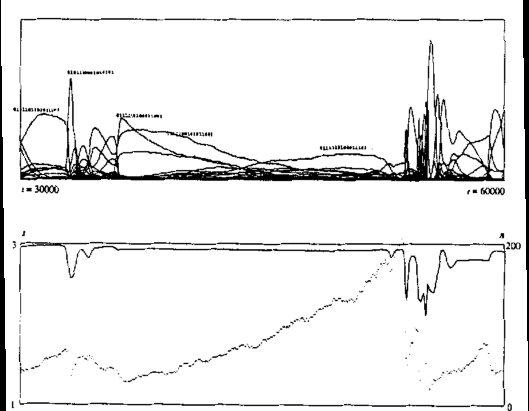
- Lindgren's experiments show stasis, punctuated equilibria, varying speeds of
evolution, mass extinctions, symbiosis, and complexity increase. Unlike Axelrod's
and Rappoport's results previously, these experiments show that TFT is not
evolutionarily stable as there are strategies which play as well with TFT but better
against other strategies.
- Experiments:
- Evolution of strategies of memory 1. See below.
- Evolution of strategies of memory 2 and 3. See figure below.
- Evolution of strategies of memory 4 and beyond. See figure below.
- Other related work.
- Karl Sigmund [1993] offers a very interesting overview of the original work by
Axelrod and Rappoport on the IPD.
- Melanie Mitchell [1996] and Klaus Emmeche [1994] offer an overview of
Lindgren's experiments.
- There is no evolutionary stable strategy in IPD [Boyd and Loberbaun,1987; Farrell
and Ware, 1989]
- Including Choice and Refusal of Game Players increases the emergence of
cooperation and results in more interesting modeling of negotiation strategies as
discovered by Stanley, Ashlock and Testfatsion, [1994]. This addition to the IPD tough
not a tremendous computational extension, offers a qualitatively different way of modeling
choice in the framework of the IPD. In this implementation, agents can refuse to play with
other agents given a past history of encounters. This addition can be seen to increase the
degree of dynamical incoherency between agents and their environment comprised of
other agents as agents can opt to decouple themselves from the on-going strategy
dynamics. Not surprisingly, this extension results in higher cooperation as agents can
choose to play only with other cooperating agents, thus obtaining higher payoffs.
- Violating the second rule of the PD payoff scheme yields (as expected) strategies that take
turns exploiting one another [Angeline, 1994]
- Cooperation also emerges in non-iterated PD in spatially arranged environments [Oliphant,
1994]. In this implementation, agents play the game with other agents in their
neighborhood. This allows us to study the emergence of spatially distributed families of
strategies.
The agents in the models described in this section possess more interesting environments with
changing or non-trivial demands. The objective of these models is to study how learning and
knowledge can interact with evolution.
The Baldwin Effect (organic selection): If learning helps the survival of organisms (more plastic
behavior) then this trait should be selected. If the environment is fixed, so that the best things to learn
remain fixed, the learned knowledge may be eventually genetically encoded via natural selection.
Example: animals capable of learning to avoid a new predator or other environmental danger, will
survive long enough to allow genetic variation to eventually discover that avoiding the danger is
useful trait to possess at a instinctual, genetically determined level. Waddington [1942] referred to
this process as genetic assimilation.
- Hinton and Nowlan [1987] Experiments: Agents were modeled by a very simple
neural network and evolution was modeled by a Genetic Algorithm:
- 1000 encoded neural nets with 20 potential connections. A connection can be
present (1 25%), absent (0 25%), and learnable (? 50%).
- Crossover, no mutation.
- Fitness: only one layout of 0's and 1's can solve the environment's problem (all
others have 0 fitness) 220 possibilities.
- If an agent has incorrect 1 or 0 it will never solve the problem, but those
with ?'s have the capacity to learn the correct pattern in 1000 learning trials
- fitness function: (1 + 19n/1000). tradeoff between efficiency and plasticity.
- "Learning" algorithm: Random guessing (network guesses at each trial the value of
its connections). It is not a proper algorithm but it allows the modeling of the
plastic nature of knowledge.
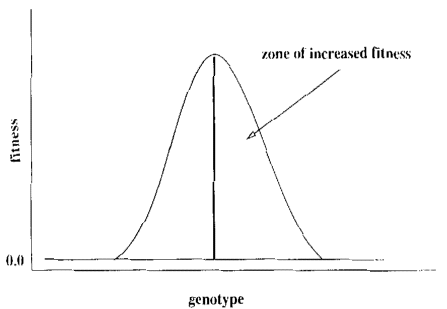
- Without learning the fitness landscape would be a single spike, with the plasticity
of learning it becomes a smoother curve (figure below).
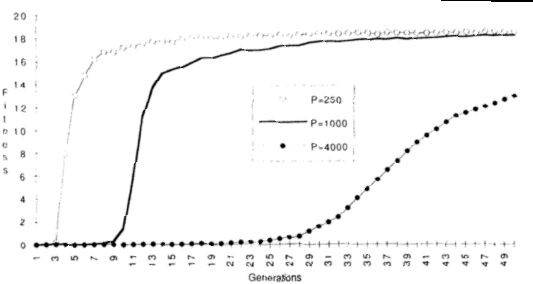
- Fitness never increases in runs without learning, but there is convergence to the
solution when learning is introduced (figure below, from [Belew, 1990]).
- Learning can be a way for genetically coded partial solutions to get partial credit,
allowing evolving agents to survive long enough for natural selection to discover
the genetic solutions. Belew [1990] showed that after long runs, the number of
unfixed positions (?) in the agents' networks decreases, as individuals with
genetically encoded correct 1's and 0's eventually appear.
- These experiments show that even such trivial learning processes as random
guessing in simple neural networks, will yield advantages to evolving agents in
very harsh environments. Leaning provides ontogenetic plasticity to practically
impossible phylogenetic solutions.
- Evolutionary Reinforcement Learning, [Ackley and Littman, 1991]. This model is a
much more complicated exploration of the interactions between learning and evolution. It
relies on an environment with no explicit evolutionary fitness function. Furthermore,
unlike a genetic algorithm, agents in a population do not reproduce on every single
generation, but only when certain necessary conditions are met. Agents are in this sense
asynchronous. This imbues the model with a certain degree of dynamical incoherency
between agents rules and environment laws which is both more realistic and important to
model decision processes. Another very important aspect of the agent architecture in this
model, is the distinction between innate, unchangeable, evaluation rules which denote the
agents' "dispositions" or "beliefs" about their situation in the environment and the actual
rules of behavior that can change in the lifetime if the agents. A similar architecture seems
to be most appropriate to model decision processes for the agent models we envision for
this project - even without an evolutionary component.
- The model:
- Agents in a 2-D environment with food, predators, hiding places, etc.
- Agent architecture with 2 feedforward neural networks:
- Evaluation net: gets agent state as input, produces judgement of how good
state is. Fixed from birth (innate dispositions, goals and desires).
- Action net: gets agent state as input, produces a move command (which
can have many outcomes). Weights changed during lifetime with
backpropagation/reinforcement learning algorithm. Implements the
behavior of agents.
- Fixed Architecture: only weights change for agents.

- The evolutionary algorithm uses genetic descriptions for each agent. These
descriptions encode (84) weights (of 4 bits) for networks (336 bits).
- Agents have an energy gauge and die for low values. They must find food
to keep energy at viable levels. Agents can only reproduce with enough
energy.
- Agents can reproduce asexually with mutation only and sexually when
neighbor exists, with crossover and mutation.
- Fitness emerges from environment and not from a pre- specified function
(artificial life model).
- At each step of the computation the difference between current and previous
evaluation is the reinforcement signal to modify weights of the action net. This
way, agents learn to act in ways that lead to states "deemed" better by the agent's
own innate evaluation net.
- Agents then move based on the adjusted weights of action net.
- Performance: time to extinction of a population.
- Results: Evolution alone (E) was not much better than random motion (B).
Learning plus evolution (ERL) was not much better than learning alone (L). The
authors propose that it is easier to generate randomly a good evaluation function
than a good action function, since the latter network is simpler. This way, in runs
without learning, the evolutionary algorithm cannot find a good behavior network.
This is similar to the previous model: the environment is too harsh for evolution.
On L runs, conversely, a good evaluation net is usually generated at random
initially, and learning is then able to produce a good action bet, while evolution
alone can not produce a good action net.
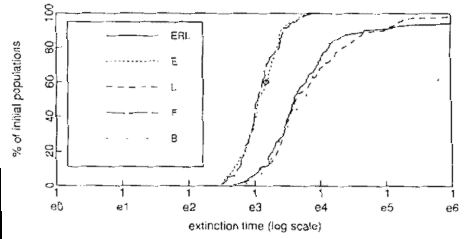
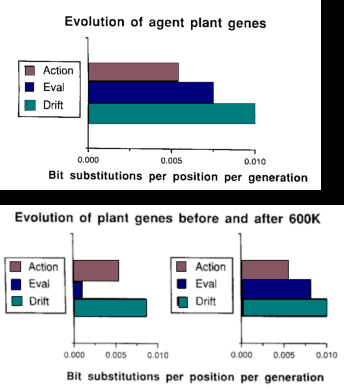
- Interactions between learning and evolution. The authors used functional
constraints analysis, a traditional technique of evolutionary biology which studies
the rate of change of different parts of the genome, to gain deeper knowledge
about this model. This analysis centers on the notion that the more fixed parts of
the genome are assumed to be important for survival during a given period. They
observed genes associated with actions concerning food, evaluations concerning
food, and genes coding for nothing (inserted for this sake):
- Naturally, non-coding genes have the highest rate of mutation.
- Evaluation genes mutate more, which implies that action genes are more
functionally constrained. However, during the first stages of the simulation,
evaluation genes are much more stable. Action genes become constrained
later. This leads us to conclude that learning is essential in the first stages
of the modeling experiment, but genetically encoded behavior for actions in
the environment becomes more functionally constrained in latter stages:
evidence for the Baldwin effect.
Another class of models with interest to our problem area deals with the emergence and evolution
of communication among agents with no explicitly programmed ability to communicate.
- Emergent Particle Computation. Crutchfield and Mitchell [1995]. In this model,
"agents" are simple boolean automata organized in a spatial one-dimensional lattice, or 1-D cellular automata (CA). The CA needs to solve a non-trivial task such as the density
task: When the initial state of the whole lattice contains a majority of automata/agents
with state=1 (0), then the whole lattice should converge to an all-1 (0) state. This is a non-trivial task because each agent has access solely to local information, namely the states of
its neighbors, yet the lattice as a whole is expected to perform a global task. Clearly, the
task can only be solved with some amount of information integration across the lattice.
The experiments were set up in the following way:
- Lattices of 149 (599, 999) boolean agent automata with boolean rules of radius 3
(7 cells in neighborhood).
- A Genetic Algorithm (GA) was used to evolve rules to solve this
task/environment.
- A typical result from running the GA is the block-expansion rule (figure below).

- But occasionally a rule emerges that can solve this task with much better results.
These rules create an intricate system of lattice communication. Groups of adjacent
automata propagate certain patterns across the lattice, which as they interact with
other such patterns "decide" on the appropriate solutions for the lattice as a whole.
An intricate system of signaling patterns and its communication syntax has been
identified, and can be said to establish the emergence of embedded-particle
computation in evolved CA's [Crutchfield and Mitchell, 1995, Hordijk et al,
1996]. The emergent signals (or embedded particles) refer to the borders of the
different patterns that develop in the space-time diagrams. If the areas inside these
patterns are removed, their boundaries can be identified as a system of signals with
a definite syntax, or emergent logic grammar. This syntax is based on a small number of signals, α, β, δ, γ, η, and μ, and a small number or rules such as: α + δ → μ, meaning that when signals α and δ collide, the μ signal results. See
Figure below.
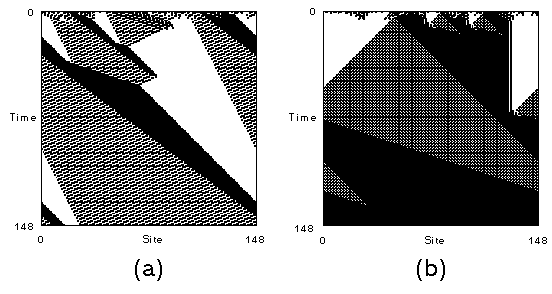
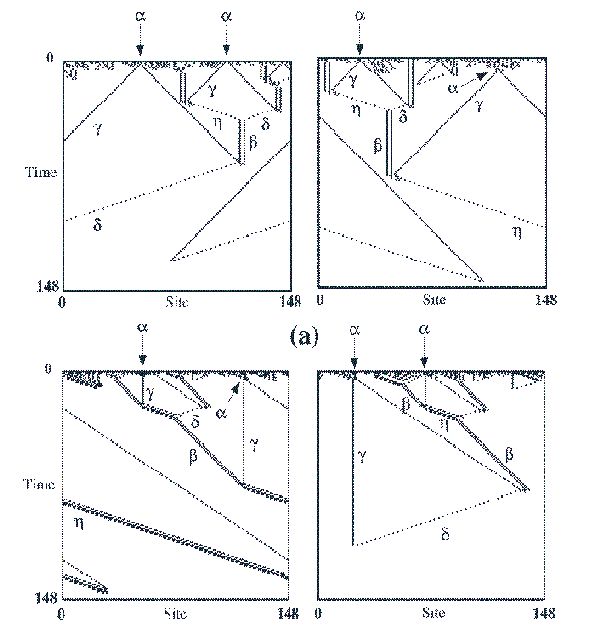
- The system of particle computation uses signals that are capable of integrating
distant global information to solve the task. These CA rules rely on a system of
signals used to communicate across the lattice and compute the answer to the task:
an autonomous sign system that grants great selective advantage to the rules
capable of developing it. The particle computation system truly introduces a
qualitatively different way of solving the task: through the emergence of
autonomous syntax, which allows certain rules to gain access to global lattice
information [Rocha, 1998].
- Rocha[1998] has expanded these rules to solve more complicated tasks such as
logical operations.
- Evolution of Communication.
- Werner and Dyer [1991], developed a agent-based computer experiment in the
same line of thought as that of Ackley and Littman detailed above, to study the
evolution of communication. The environment of these agents was set up so that
blind male agents need to wander a 2-D environment in search of female agents
with sight and the capacity to emit "sounds". Each agent has a distinct genome
which is interpreted to produce a neural network that defines the agent's action
behavior. This model also does not possess an explicit fitness function for the
evolutionary algorithm. Rather, agents are given a certain amount of time to find a
mate a reproduce. This produces the desirable asynchrony as agents do not
reproduce all in the same time step. This results in overlapping generations with
the possibility of inter-generational communication - important for the evolution
and transmission of communication and knowledge. These experiments produced a
number of very interesting "species" of male-female agents tuned to their own
communication protocol or semantic closure. This model will undoubtedly also
provide good design principles for our intended simulations.
- Evolution of Learning in the Cultural Process. Hutchins and Hazlehurst [1991]
produced an agent-based computer experiment to study how communication can
and should emerge from the regularities of a given environment. The show that the
evolution of communication is based adaptation of agents' internal structures to
the structure of the environment, that is, coordination between internal and
external structure. They embed their experiments in a framework which posits that
culture is a process that permits the learning of previous generations to have direct
effects on the learning of subsequent generations. Their experiments are also
fundamentally semiotic, as they posit that the signals that enable communication of
culture must be themselves somehow "physically" implemented in a environment.
In other words, communication must itself be based on some structure that exists
between agents and the environment in addition to agent internal structure and
environmental structure. This third kind of structure is of an artifactual nature.
This way, the agents of a cultural world have their internal structure shaped by (in
coordination with) two kinds of structure in the environment: natural and
artifactual. Their experiment is set up to produce agents that may learn a language
(using a "physical code) able to mediate between environment regularities and
artifactual descriptions of them. Their model sets up a simple environment (loosely
based on ethnographic records of California Indians) where there is a relations
between moon phase and tide state, which is relevant for agents feeding on
shellfish. They use a cultural selection algorithm on agents that possess different
neural networks for behavior and knowledge. They show that with the availability
of artifactual structure, the learning of the relationship between moon phase and
tide state is much more easily discovered and propagated in the population of
agents. This model will undoubtedly also provide good design principles for our
intended simulations.
- Similar experiments based on culture and language were also performed by
MacLennan [1991].
The last models of section 3.3 in their dealing with the evolution of communication, rely on the
evolution of common structures among agents used to enable communication, e.g. artifactual
structures. In this section we deal with models whose goal is to explicitly study the nature and
consequences of such shared structure among agents. Being more explicit, these models emanate
more from artificial intelligence, social science, and game theory, than from artificial life as the
previous models did.
- The Collective Choice Model of Richards, McKay, and Richards [1998]. This model
aims at the investigation of a fundamental problem of social choice models, particularly
those used to model collective choice of political alternatives. Previously, it has been
showed [e.g. Arrow, 1963, McKelvey, 1979] that the aggregation of elements into a
collective choice when many agents and possible choices are involved typically leads to
unstable, cyclic outcomes - for instance when we implement majority vote rules on
automata. This is clearly at odds with reality where societies are capable of reaching stable
political outcomes even in political systems with many available choices. The authors
claim that such cyclic behavior exists because the previous system used to study collective
choice do not make use of appropriate common structure among agents (this claim is in
line with the models of the previous section). Indeed, agents in previous models are
assumed to make their own choices autonomously. The authors show mathematically and
computationally that by establishing a shared knowledge structure, the probability of such
cyclic behavior is reduced dramatically (figure below).
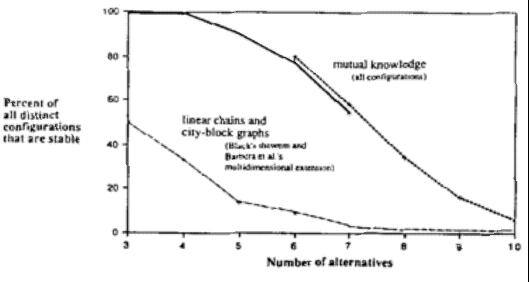
- The shared knowledge structure is implemented as a graph structure among
alternatives. Such a graph implements the regularities of a particular choice
landscape or environment. It is very reasonable to assume that alternatives are not
all equally related (or un-related), but possess some structure. For instance, when
deciding what kind of movie we want to watch, we all share some common
knowledge: we know that a horror movie is more related to a violent action movie
than to a romantic comedy. Likewise, we know that a Christian-democrat party is
more related to a social democrat than to a communist party.
- The shared knowledge structure implemented as a graph effectively establishes
constraints on the choices which implement the regularities of a given choice
system.
- From the shared knowledge structure, different partial orders can be established to
represent agents with different dispositions towards the shared knowledge
structure. For instance, agents who prefer romantic comedies to horror movies,
etc. See figure below.
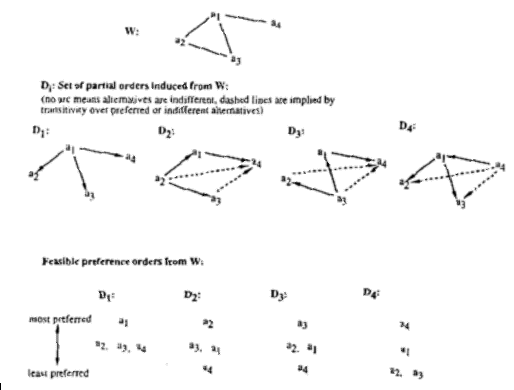
In agent-based simulation agents interact in an artificial environment. However, it is often the case
that the distinction between agents and environments is not clear. In contrast, in natural environments,
the self-organization of living organisms is bound and is itself a result of inexorable laws of physics.
Living organisms can generate an open-ended array of morphologies and modalities, but they can
never change these laws. It is from these constant laws (and their initial conditions) that all levels of
organization we wish to model, from life to cognition and social structure, emerge. These levels of
emergence typically produce their own principles of organization, which we can refer to as rules, but
all of these cannot control or escape physical law and are "neither invariant nor universal like laws"
[Pattee, 1995b, page 27].
The question of what kinds of rules can emerge from deterministic or statistical laws is at the core
of the field of Artificial Life [Langton, 1989]. It is also very much the question of generating and
studying emergent semantics and decision processes in artificial environments - which we are
interested in. However, "without principled restrictions this question will not inform philosophy or
physics, and will only lead to disputes over nothing more than matters of taste in computational
architectures and science fiction." [Pattee, 1995b, page 29] For agent-based simulations to be
relevant for science in general, the same categories of laws/initial conditions and rules that we
recognize in the natural world, need to be explicitly included in an artificial form. For more arguments
for the need to explicitly distinguish laws and rules in artificial environments please refer to [Rocha
and Joslyn, 1998].
Therefore, the setup of environments for multi-agent simulations needs to:
- Specify the dynamics of self-organization: specify laws and their initial
conditions, which are responsible for the characteristics of the artificial
environment (including agents) and the emergence of context-specific rules.
- Example: In Lindgren's [1991] experiments described in section 3.1.1, the
laws of the system are the conditions specified in the iterated prisoner's
dilemma and the genetic algorithm - these are inexorable in this simulation.
The context-specific rules are the several strategies that emerge whose
success depends on the other strategies which co-exist in the environment
and therefore also specify its demands together with the laws. However,
the same laws can lead to different transitory rules, and thus, different
agent environments.
- Observe emergent or specify constructed semantics: identify emergent or pre-programmed, but changeable, rules that generate agent behavior in tandem with
environmental laws. In particular, we are interested in the behavior of agents that
can simulate semantics and decision processes.
- Example: The experiments of Hutchins and Hazlehurst described in section
3.3 clearly separate between the laws of the agents' environment (the
regularity of tide and moon states) and the artifacts used by the agents to
communicate the semantics of these regularities among themselves. The
semantics of the artifacts emerges in these simulations.
- Provide a pragmatic selection criteria: create or identify a mechanism of selection
so that the semantics identified in ii is grounded in a given environment. This
selection criteria is based on constraints imposed both by the inexorable laws of the
environment and the emergent rules. When based only on the first, we model an
unchanging set of environmental demands (explicit selection), while when we
include the second, we model a changing set of environmental demands instead
(implicit selection).
- Example. Typically the selection criteria is implemented by an evolutionary
(genetic or cultural) algorithm with implicit or explicit evaluation function.
The explicit function is seen in Hinton and Nowlan experiments, while the
implicit function is seen in Ackley and Littman's experiments, both in
section 3.2.
A good example of experiments that use the three requirements above are the emergent computation
experiments on Cellular Automata (CA) [Mitchell and Crutchfield, 1995] with Genetic Algorithms
(GA's), described in section 3.3. Agents (each modeled by an automaton) are constrained to an one-dimensional lattice (the CA) and to a fixed automata production rule , which defines the lower-level
virtual laws that lead to emergent behavior in such an environment. The emergent behavior produces
different higher level structures to deal with environmental demands, sometimes producing an
emergent semantics with a primordial syntax (e.g. particle computation): these are the higher-level,
changing rules. Finally, there is an environment which requires a non-trivial task to be performed. The
selection mechanism implemented by the GA is an explicit selection function, which directs the self-organization of rules from laws that cope well with the fixed environment.
These three requirements establish a selected self-organization principle [Rocha, 1996, 1998, 199?]
observed in natural evolutionary systems. This principle is also essential to model the emergence of
semantics and decision processes in agent-based simulations which can inform us about natural world
phenomena. Essential because without an explicit treatment or understanding of these components
in a simulation, it is impossible to observe which simulations results pertain to unchangeable
constraints (laws), changeable, emergent, constraints (rules), and selective demands. It is often the
case in Artificial Life computational experiments that one does not know how to interpret the results
- is it life-as-it-could-be or physics-as-it-could-be? If we are to move these experiments to a
modeling and simulation framework, then we need to establish an appropriate modeling relation with
natural agent systems which are also organized according to laws, rules, and selection processes.
The design of semiotic agent models that we are interested in, build up some of the architectures
presented in the review above. Semiotic agents, as we see them, need to be based on a few
fundamental requirements:
- Asynchronous behavior. In our models, agents do not simultaneously perform
actions at constant time-steps, like CA's or boolean networks. Rather, their actions
follow discrete-event cues or a sequential schedule of interactions. The discrete-event setup allows for inter-generational transmission of information, or more generally, the cohabitation of agents with different environmental experience. The
sequential schedule setup, formalized by Sequential Dynamical Systems (SDS)
[Barrett et al, 1999], allows the study of different influence patterns among agents,
very important to study decision processes in social networks. The latter are ideal
for mathematical treatment as different schedules can be studied in the SDS
framework, while the former require statistical experimentation as the collective
behavior of discrete-event agents in an environment with stochastic laws and rules
cannot be easily studied mathematically.
- The discrete-event agent designs we are interested in build on the agents of
Ackley and Littman [1991] and the models of the evolution of
communication of Werner and Dyer [1991] and Hutchins and Huzlehurst
[1991] of 3.2 and 3.3.
- The sequential schedule agent designs uses the SDS framework
supplemented with the additional points below.
- Situated Communication. We require that communication among agents be based
on the existence of environmental tokens and regularity which must follow the
laws of the environment and agent rules. Communication must use resources
available in the environment which follows laws and rules, and not rely on
unconstrained, oracle-type, universal channels.
- This is very much in line with the artifactual nature of communication in
Hutchins and Hazlhurst [1991] experiments, or the CA's of Crutchfield and
Mitchell [1995] in section 3.3.
- Shared and cultural nature of language and knowledge. We require that agents
share a certain amount of knowledge. This way, agents are not completely
autonomous entities with their own understanding of their environments. We are
interested in studying social systems which strongly rely on shared knowledge
expressed in public languages. Often, in agent-based models, agents reach
decisions resting solely on personal rules and knowledge-bases. This autonomous
view of agency is unrealistic when it comes to modeling cognitive and social
behavior, as ample evidence for the situated nature of cognition and culture [Clark,
1998; Richards et al, 1998; Beer, 1995; Rocha, 1999].
- Therefore, our agents build on the graph structures used by Richards et al
[1998] to model shared knowledge as described in section 3.4. In particular
we expand this framework with the asynchrony (i) and situated
communication (ii) agent design requirements. In a sense, combining the
models of Richards et al, Hutchins and Hazlehurst [1991] and Werner and
Dyer [1991]. We also study emergent shared knowledge structures.
- Capacity to evaluate current status. Since a goal of agent-based simulations of
social systems is to study decision processes, our agents need to include a means
to describe their own preferences and beliefs. This way, agents need to have
separate behavior components for action and evaluation. The evaluation
component is used by the agent to judge its current status in the environment and
then influence the action component. These components can be created and/or
evolved independently. This way, we can model agents with different, independent
beliefs about their present state and desirable goals.
- This capacity is present in the agents of Ackley and Littman (which are
similar to those of Werner and Dyer and Hutchins and Hazlhurst).
However, our evaluation components are further constrained by shared
knowledge structures and situated communication.
- Stable, decoupled memory. To model more realistically decision processes, and
achieve greater dynamical incoherence between agents and environments, we need
to move from state-determined behavior components and endow agents with
larger, random-access, memory capacity. This implies the storage of a set agents'
interactions in memory to aid its evaluation and action behavior. These memory
banks persist and can be accessed at any time by the agent, and do not depend on
its current state or the state of the environment.
Given the environment and agent requirements of 4.1.1 and 4.1.2, we can now discuss the extent of
the dynamical incoherency of semiotic agents as described in section 1. Clearly, the multi-agent
systems with the requirements above possess elements of dynamical coherency and dynamical
incoherency. The dynamic laws of the environment spawn rules of agent behavior which are this way
dynamically coupled to the environment. The dynamical incoherence occurs with the following
knowledge requirements:
- Shared knowledge structures which persist in the environment through at least for
long intervals of dynamic production;
- Semantic tokens/artifacts required by situated communication, which persist in the
environment, at least for long intervals of dynamic production, until they are
picked up by agents;
- The stable memory banks used by agents to store knowledge are decoupled from
the dynamics of the environment.
Note that the asynchrony requirement does not necessarily imply dynamical incoherence. Discrete-event or schedule-driven agents may or may not respond to their cue events or schedules in a
dynamical coherent or incoherent manner. If their action and evaluation components are state
determined, as the agents of Ackley and Littman or the SDS framework, then they are still
dynamically coupled to their environment and its cues. It is only the knowledge requirements which
can create a degree of dynamical incoherency, as memory gets decoupled from state-determined
interaction.
- The asynchrony and situated communication agent requirements establish
localized constraints on communication and event-driven actions among agents.
We wish to investigate the nature of these constraints. We expect these constraints
to be similar to the shared knowledge constraints of the model of Richards et al
[1998]. Notice that this model is based on synchronous updating. We postulate
that asynchrony and situated communication will result in the emergence of a
shared knowledge structure with the same characteristics of Richards' et al
model. Situated communication and asynchrony will implement the realistic
situation of having agents' choice be dependent on the choice their neighbors have
pursued earlier as well as on the events in their neighborhood. This would be an
important theoretical result for the study of choice models.
- We wish to investigate the relative effect of the 5 agent design requirements on
networks of influence in multi-agent social models. Particularly, different
discrete-event and scheduling schemes will lead to different influence patterns.
But, all other environment and agent requirements will play a role in these
patterns.
- Partial shared knowledge structures. What is the effect of agents possessing only
a subset of the overall shared knowledge structure in a given multi-agent system.
- We also wish to study possible disruption to communication and influence
networks. For example, how dependent on situated communication tokens is the
stability of a social structure?
- How does the size of the stable memory of agents affects the behavior and
stability of the multi-agent system?
- How important is the evaluation component in a given multi-agent setup? How
can it be influenced by other agents?
Ackley, D.H. and M. Littman [1991]."Interaction between learning and evolution." In: Artificial Life II. Langton et
al (Eds). Addison-wesley, pp. 487-509.
Angeline, P.J. [1994]."An alternate interpretation of the iterated prisoner's dilemma and the evolution of non-mutual cooperation." In: Artificial Life IV. R. Brooks and P. Maes (Eds.). MIT Press, pp. 353-358.
Arrow, K.J. [1963]. Social Choice and Individual Values. .
Belew, R.K. [1990]."Evolution, learning, and culture: computational metaphors for adaptive algorithms." Complex
Systems. Vol. 4, pp. 11-49.
Boyd, R., and J.P. Loberbaum [1987]."No pure strategy is evolutionarily stable in the repeated Prosiner's Dilemma
game." Journal of Theoretical Biology. Vol. 136, pp. 47-56.
Crutchfield, J.P. and M. Mitchell [1995]."The evolution of emergent computation." Proc. National Acadamy of
Sciences, USA, Computer Sciences. Vol. 92, pp. 10742-10746..
Emmeche, Claus [1994]. The Garden in the Machine: The Emerging Science of Artificial Life. Princeton
University Press.
Farrell, J., andR. Ware [1989]."Evolutionary stability in the repeated Prisoner's Dilemma." Theoretical Population
Biology. Vol. 36, pp. 161-166.
Hinton, G.E. and S.J. Nowlan [1987]."How learning can guide evolution." Complex Systems. Vol. 1, pp.495-502.
Holland, J.H. [1995]. Hidden Order: How Adaptation Builds Complexity. Addison-Wesley.
Hordijk, W., J.P. Crutchfield, and M. Mitchell [1996]."Embedded-particle computation in evolved cellular
automata." In: Proceedings of Physics and Computation 96. . In Press. Available as a Santa Fe Institute
preprint (96-09-073).
Hutchins, E. and B. Hazlehurst [1991]."Learning in the cultural process." In: Artificial Life II. C. Langton, C.
Taylor, J.D. Farmer, and S. Rasmussen. Santa Fe Institute studies in the sciences of complexity series.
Addison-Wesley, pp. 689-706..
Lindgren, K. [1991]."Evolutionary Phenomena in Simple Dynamics." In: Artificial Life II. Langton et al (Eds).
Addison-wesley, pp. 295-312.
MacLennan, B. [1991]."Synthetic Ethology: An Approach to the study of communication." In: Artificial Life II.
Langton et al (Eds.). Addison-wesley, pp. 631-558.
McKelvey, R.D. [1979]."General conditions for global intransitivities in formal voting models." Econometrica.
Vol. 47, pp. 1085-112.
Mitchell, Melanie [1996]. An Introduction to Genetic Algorithms. MIT Press.
Oliphant, M. [1994]."Evolving cooperation in the non-iterated prisoner's dilemma: the importance of spatial
organization." In: Artificial Life IV. R. Brooks and P. Maes (Eds.). MIT Press, pp. 349-352.
Pattee, Howard H. [1993]."The limitations of formal models of measurement, control, and cognition." Applied
mathematics and computation. Vol. 56, pp. 111-130.
Richards, D., B.D. McKay, and W.A. Richards [1998]."Collective choice and mutual knowledge structures."
Advances in Complex Systems. Vol. 1, pp. 221-236.
Rocha, Luis M. and Cliff Joslyn [1998]. "Simulations of Evolving Embodied Semiosis: Emergent Semantics in Artificial
Environments" Simulation Series; Vol. 30, (2), pp. 233-238..
Rocha, Luis M. [1996]."Eigenbehavior and symbols." Systems Research. Vol. 13, No. 3, pp. 371-384.
Rocha, Luis M. [1998]."Selected self-organization and the Semiotics of Evolutionary Systems." In: Evolutionary
Systems: Biological and Epistemological Perspectives on Selection and Self-Organization. S. Salthe, G.
Van de Vijver, and M. Delpos (eds.). Kluwer Academic Publishers, pp. 341-358.
Rocha, Luis M. [1998]."Syntactic Autonomy." In: Proceedings of the Joint Conference on the Science and
Technology of Intelligent Systems (ISIC/CIRA/ISAS 98). National Institute of Standards and Technology,
Gaithersbutg, MD, September 1998. IEEE Press, pp. 706-711.
Rocha, Luis M. [1999]. "Syntactic autonomy, cellular automata, and RNA editing: or why self-organization needs
symbols to evolve and how it might evolve them". New York Academy of Sciences. In Press.
Sigmund, K. [1993]. Games of Life: Explorations in ecology evolution and behavior. Oxford University Press.
Stanley, E.A., D. Ashlock, and L. Tesfatsion [1994]."Iterated Prisoner's dilemma with choice and refusal of
partners." In: Artificial Life III. C.G. Langton (Ed.). Addison-Wesley, pp. 131-175.
Werner, G.M. and M. G. Dyer [1991]."Evolution of Communication in Artificial Organisms." In: Artificial Life
II. Langton et al (Eds). Addison-wesley, pp. 659-687.
Footnotes
1. Defect if opponent defected last, cooperate if opponent cooperated last. Start by
cooperating.