Citation: Rocha, Luis M. [2001]. "Evolution with Material Symbol Systems".Biosystems. Vol. 60, pp. 95-121. LAUR 00-1604.
This paper is also available in Adobe Acrobat (.pdf) format, or from Elsevier's web site
Note: The HTML version of this paper has a few small errors in Table I and the definition of some parameters. The pdf version has been updated with corrections.
Abstract: Pattee's semantic closure principle is used to study the characteristics and requirements of evolving material symbols systems. By contrasting agents that reproduce via genetic variation with agents that reproduce via self-inspection, we reach the conclusion that symbols are necessary to attain open-ended evolution, but only if the phenotypes of agents are the result of a material, self-organization process. This way, a study of the inter-dependencies of symbol and matter is presented. This study is based first on a theoretical treatment of symbolic representations, and secondly on simulations of simple agents with matter-symbol inter-dependencies. The agent-based simulations use evolutionary algorithms with indirectly encoded phenotypes. The indirect encoding is based on Fuzzy Development programs, which are procedures for combining fuzzy sets in such a way as to model self-organizing development processes.
Keywords: Howard Pattee, Evolutionary Systems, Evolutionary Algorithms, Artificial Life, Biosemiotics, Genetic Algorithms, Fuzzy Set Theory, Agent-Based Simulation, Representation.
Howard Pattee's main contribution to science and philosophy has been his insistence on complementary modes of description in models of the living organization. He has proposed that models of biological systems based solely on physical law, do not explain the symbolic nature of genetic descriptions. Conversely, models of the biological organization that are based solely on the symbolic nature of genes, miss the material constraints observed by any physical system, which are also fundamental to biology. The term semantic closure (Pattee, 1982, 1995a) was used to convey a principle of organization of living systems, which requires symbolic and material modes of description, and is necessary to achieve open-ended evolution.
The skepticism and rejection that this principle often encounters in Theoretical Biology, Artificial Life, and Complex Systems research lies both on the notions of material symbol systems (MSS) and open-ended evolution (OEE). Many have doubts about what kind of physical processes constitute a MSS used to manipulate representations or descriptions. Due to long standing debates in Cognitive Science, where physical symbol systems have come to be identified with a functionalist approach, which deems irrelevant the materiality of a physical symbol system, many believe that the notions of symbol and representation are unnecessarily murky - or even mystical and dualist. Indeed, since we can study evolutionary processes with Dynamical Systems Theory (DST) (1), why should we confuse things with symbols and semiosis? Those that profess this point of view claim that we should use DST exclusively as the explanatory tool for evolutionary systems, which in this sense would be modeled only with physical law and self-organization as captured by DST (Beer, 1995; Van Gelder and Port, 1995; Maturana and Varela, 1987; Goodwin, 1994).
In contrast, Pattee argues that only MSS are capable of OEE. Other material systems can evolve, but not in an open-ended manner. But what constitutes a MSS, and what is OEE? Pattee uses the genetic machinery of the cell as an example of the former, and evolution by natural selection as an example of the latter. But our knowledge of molecular biology is still very incomplete to allow a theoretical treatment of these individual topics. Therefore, in order to strengthen his argument, one needs first to define the material symbol systems which follow the semantic closure principle, and then discuss evolutionary processes in order to identify those that are open-ended from those that are not. In this article I elaborate on these distinctions, and present experiments with simulated simple matter-symbol systems to validate some of mine and Pattee's assertions.
In particular, I will provide arguments and experimental evidence that even though material systems cannot evolve in an open-ended manner without symbols, OEE is not a result of symbols alone, but of the complex interplay between symbols and matter. Often Pattee's semantic closure is seen as a non-materialist organization principle, but as we shall see, quite the contrary is true. Notice also that OEE here is not discussed by contrasting simulations with realizations of evolving systems as Cariani (1992) and Pattee (1989) did. Rather, the contrast is between a fully dynamicist and a complementary symbolic/dynamicist view of evolutionary systems. Furthermore, this contrast is exemplified with both biological knowledge and computer simulations.
I will start by discussing evolving material agents and the possible types of reproduction such agents need to pursue in order to evolve. By contrasting the evolutionary potential of different reproduction strategies, I reach Pattee's conclusion that only MSS are capable of attaining OEE. From here, I present the arguments for the inclusion of semiotics in models of evolutionary systems and outline a set of requirements for MSS. Finally, I describe simulations of evolutionary processes in populations of agents with and without replication via MSS. These simulations offer a means to study simple matter-symbol systems and their evolutionary potential empirically.
To introduce symbols in the explanatory framework of biology, instead of starting from the cognitive top, Pattee (1982), suggested that we start from the simplest symbol-matter systems at the bottom of the biological organization. If we are to refer to some material systems as symbolic, we need to start from the physical milieu to decide when some arrangement of material components becomes symbolic.
We typically study the physical law of material systems with mathematical theories such as DST. This dynamics approach leads to the notion of self-organization. Self-organization is seen as the process by which energetically open systems of many components tend to reach a particular state, a set of cycling states, or a small volume of their state space (attractor basins), with no external interference. This attractor behavior is often recognized at a different level of observation as the spontaneous formation of well organized structures, patterns, or behaviors, from random initial conditions (emergent behavior, order, etc).
Self-organization is studied computationally with discrete dynamical systems (state-determined systems) such as boolean networks or cellular automata. The state-determined transition rules are interpreted as the laws of some physical system (Langton, 1986; Rocha and Joslyn, 1998): the state of each component depends on the states of its neighboring (or related) components in the previous time instance. It follows from the observed attractor behavior (Wuensche and Lesser, 1992) that there is a propensity for matter, whose physical law is modeled by the transitions rules of DST, to self-organize (e.g. Kauffman, 1993). In this sense, matter is described by the (lower-level) laws of physics (which can be modeled computationally with DST) and the observed (emergent) attractor behavior of self-organization.
Several characteristics of the emergent behavior of systems comprised of many interacting material components have lead to them being named complex (Pattee, 1973). Typically, from the final attractors, we cannot recover the initial configuration of states of the system's components (its initial conditions). In other words, the emergent organization of (complex) self-organizing systems is non-linear or irreversible, as we cannot separate the individual contributions of its building blocks, even though we may be able to distinguish the building blocks themselves. These characteristics of self-organizing material systems are modeled in section 5.
Another important characteristic of self-organizing systems is that they are dynamically coupled to their environment. In the language of physics, we can say that the system is dynamically coherent with its environment. Dynamically, a self-organizing network of components and its environment are in fact one system, a change of state in one produces a coordinated, state-determined chain of events in the other - there is a definite temporal relation between events and components of the system-environment coupling. Indeed, the self-organizing behavior of agents defined by networks of components that are dynamically coherent with their environments (situated agents) is as much a result of the production rules of the agent's components as of the laws of the environment (Beer, 1995; Clark, 1997; Rocha and Joslyn, 1998). Wheeler and Clark (1999) refer to this lack of separation between dynamically coherent agents and their environments as causal spread.
To evolve in a changing environment, self-organizing agents must be able to change their own dynamics in order to produce new basins of attraction leading to new behaviors (or phenotypes): variation. Furthermore, the most appropriate changes in a given environment need to be selected for evolution to occur. Evolution, as we know it, is based on a process of selected self-organization (Rocha, 1996, 1998), where self-organizing agents reproduce subjected to variation and those variations which are most appropriate for the demands of their environment are selected, that is, undergo an increase of their reproduction rates. Thus, self-organizing agents produce new behaviors (evolve) by reproducing themselves with variation while subjected to environmental selection. But for selection to occur the self-organizing agents must have some internal vehicle for producing and reproducing different dynamic configurations -- there must be different alternatives.
Notice that DST (modeling physical law) does not allow for alternatives. "The only meaning we can attach to a choice of alternatives in a system described by deterministic laws is through measurement and control on initial conditions". (Pattee, 1995a, page 15) In state-determined models, a choice can only be modeled by the introduction of new or change of existing initial conditions (measurement and control). That is, for evolving self-organizing agents to reproduce alternative dynamic configurations (or phenotypes), they need a process of accessing the initial conditions that produce those. When initial conditions are selected they re-enter the dynamics, self-organizing into the respective dynamic configurations (with some variation). Therefore, models of evolution must describe both the dynamics of matter and the processes used by evolving agents to access their own initial conditions for reproduction, variation and selection of new phenotypes. This notion of selected self-organization leads us to question what kinds of processes to access initial conditions are possible?
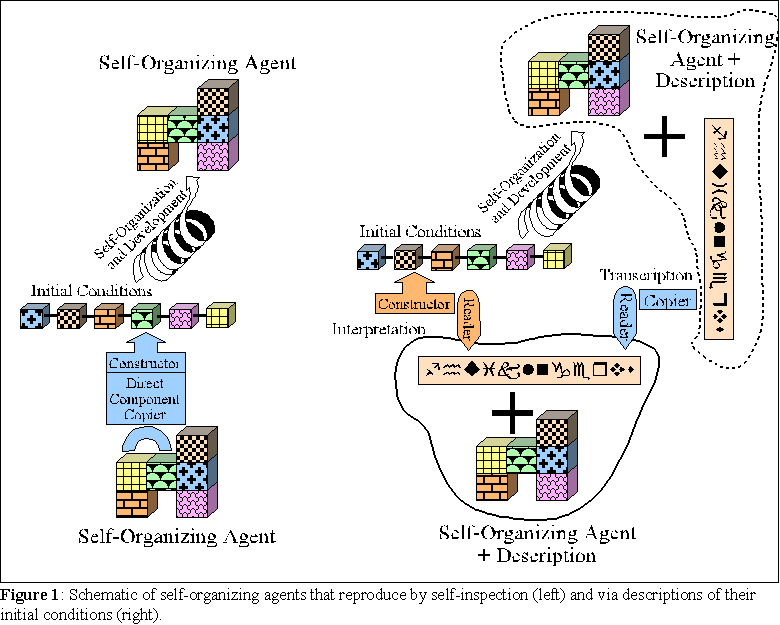
Evolution by Natural Selection is based on increased rates of reproduction of self-organizing agents whose dynamical configurations in an environment are successful. As discussed in section 2, selected dynamical configurations of agents need to be accessed as initial conditions for reproduction. Thus, agents reproduce by transmitting initial conditions to offspring, that subsequently re-produce the parents' dynamical configurations by self-organizing their material components according to the inherited initial conditions. Two distinct ways of accessing initial conditions for this transmission can be thought of: via self-inspection or via symbolic description (Von Neumann, 1966). Since biological organisms use the latter as genetic descriptions, let us first examine this type of reproduction, and then think of how reproduction via self-inspection could occur.
Von Neumann(1966) proposed a theory of self-replication as a systems-theoretic criteria for OEE (details in Rocha, 1996, 1998). It is based on the notions of universal construction and description, and it models agents which evolve by (neo-Darwinian) natural selection via variation of their genetic descriptions - though it was proposed before the DNA molecule was discovered. Von Neumann's descriptions entail a symbol system on which construction commands are cast. These symbolic descriptions are localized on "inert" structures which can be used at any time -- a sort of random access memory. In other words, symbolic descriptions store initial conditions used to construct evolving agents (modeled in his theory as cellular automata). Reproduction is achieved by simultaneously constructing the dynamical machinery of offspring and, separately, passing the "inert" description (of initial conditions) used to re-construct parents. An offspring's dynamical configuration is constructed from the initial conditions encoded in the parent's description, while its own description is copied from the parent's so that it can itself reproduce in the future. This way, the description takes an active role in constructing the offspring's dynamical configuration, and a passive role in being copied.
But what kind of material structures can be conceived of as "inert", and used as descriptions for reproducing, natural self-organizing agents? These must be material components with many dynamically equivalent states which can be used to set up an arbitrary (symbolic) relation with whatever material components that define initial conditions. The genetic system (which Von Neumann's model conceptually describes) gives us this insight. The genotype of biological organisms is a set of descriptions encoding initial conditions (amino-acid chains) for components (proteins) which self-organize to produce some dynamical configuration (phenotype). As Von Neumann conceptualized, biological reproduction is achieved by constructing the machinery of offspring from genetic description, while also simultaneously passing (copying) the genetic description itself.
Most any sequence of nucleotides is equally possible, and its informational value (genetic information) is largely independent of the particular dynamic behavior of the DNA/RNA sequence. Genetic information is not expressed in the dynamics of nucleotide sequences (RNA or DNA molecules), but is instead mediated through an arbitrary coding relation that translates nucleotide sequences into amino-acid sequences, whose dynamic characteristics ultimately express genetic information in an environment. It is precisely the dynamic irrelevance of nucleotide sequences ("inertness") that makes DNA/RNA ideal candidates for stores of genetic information (descriptions) given an arbitrary genetic code (Pattee, 1995a; Umerez, 1995). DNA qua carrier of genetic information in biological organisms is virtually dynamically incoherent with the organism/environment coupling, since the information needed to construct a given protein (the description or representation) can be retrieved at any time as much as a book can be retrieved from a library (Pollack, 1994).
Dynamically incoherent descriptions, can be seen as symbolic representations of dynamic configurations (as further elaborated in section 4), but what does dynamical incoherence mean? Ultimately, all symbolic descriptions have a material, dynamic, substrate. The point is that in systems where these descriptions are used as symbols, their dynamics is irrelevant. It is not their dynamic characteristics that elicits responses from the dynamic components of the system. Rather, it is their informational value, extracted via a coding relation (instantiated by the Ribosome, T-RNA and other machinery in the cell), which is relevant for the functioning of organisms. Indeed, recent organisms carry many of the same genes used by primordial organisms to produce the same proteins. More and more transgenetic technology pervades our life, we can use bacteria to produce human proteins such as insulin, or produce plague resistant tomatoes with proteins encoded in genes from pigs. All these facts show that in their role of information carriers, the dynamical substrate of genes (the DNA or RNA molecules) is largely irrelevant. Genes can be decoupled from a particular dynamic agent, and introduced into another where they will be used for their symbolic function, which is: the specification of initial conditions that produce particular cell dynamics, thus re-entering the dynamics of their host cells.
Now, of course, being instantiated as material structures, symbolic descriptions cannot be completely dynamically incoherent. Dynamical incoherence needs to be understood in the frame of stable existence of the whole dynamic machinery that recognizes representations of initial conditions. Genes can be read by the living cell's machinery, as long as the cell exists as such. Very much in the same way as a writing system is only useful as long as it is understood by an appropriate reading framework. Therefore, dynamical incoherence is not an absolute concept, but rather a relative one. For a given dynamics, with particular time scales, we can treat certain components as incoherent, if their dynamics are irrelevant in these time scales. We can further treat them as symbolic representations, if such dynamically incoherent components are used to specify sets of initial conditions for dynamic configurations of self-organizing agents. Pattee refers to the stable existence of such an evolving matter-symbol organization as semantic closure (Pattee, 1982, 1995a).
An alternative way for self-organizing agents to reproduce could be by self-inspection of their components. The process of accessing the necessary initial conditions for selection, would be via some dynamic machinery that would reproduce directly the components of the agent. In biological systems, a protein could replicate itself without descriptions, using some assembly system with access to a pool of existing parts (amino-acids). Instead of the ribosome, we could have some other molecular arrangement capable of directly reading a protein and producing a copy of it. This assembly machine, would need to "unfold" proteins to read their internal portions and generate copies from available amino acids (Pattee, 1995a). These unfolded copies would be the initial conditions that would then self-organize into selectable dynamic configurations. In this case, we would have the ability to construct proteins from other proteins, rather than from dynamically incoherent, genetic representations of initial conditions. This would be a dynamically coherent system for constructing proteins leading to a more Lamarckian evolutionary process (2). Alas, this is not the way life is!
Clearly, as systems grow in complexity, self-inspection becomes more and more difficult. The self-organization of the building blocks of life (amino acids) from the amino acid strings (the initial conditions) into folded proteins is only the first of many levels of self-organization of biological form. Proteins are themselves building blocks of levels ranging from macro-molecules to entire organisms and even communities of organisms. This hierarchy of levels of self-organization is known as biological development (Salthe, 1993), which, being a self-organizing process, is a complex, nonlinear, irreversible process (section 2.1). Therefore, it would be impossible to reproduce these developed higher level structures with the hypothetical protein-copier. From such complicated ensembles, we would not be able to obtain its initial conditions. If life were restricted to a protein-copier reproduction scheme, then it would be restricted to forms whose initial conditions were recoverable, that is, to simple ensembles of proteins which could be separated into constituent proteins, unfolded, copied, and then refolded. Thus, the diversity of life forms would be tremendously restricted (3).
The hypothetical self-inspection protein-copier would function as a "two-in-one" reader and constructor of dynamic configurations. But due to the complex nature of self-organization and development, the set of agents that could be reproduced this way would be severely limited to those with recoverable initial conditions. In contrast, Von Neumann's model of self-reproduction, decouples the reader and construction functions, using intermediate decoding machinery for symbolic descriptions of initial conditions. With this separation, agents reproduce not by self-inspection, but by constructing instructions encoded in descriptions. What is gained is the ability to construct any dynamical configuration from a description of its initial conditions, whether or not the initial conditions can be recoverable from self-organized products. This is what Von Neumann named universal construction.
This more sophisticated form of reproduction, based on a symbolic encoding system, is implemented in biological systems with great evolutionary success. Functional, dynamic structures do not need to be deconstructed into initial conditions, they are simply constructed from dynamically inert descriptions and available parts. With the genetic code, functional molecules can be simply folded from inert messages. This method is by far more general since any functional molecule, as well as the phenotypes in whose development process the molecule participates, can be produced from a description, or a set of descriptions, not merely those whose initial conditions can recovered to be reproduced by self-inspection from available parts.
Reproduction by symbolic description can produce any complex phenotype, whereas reproduction by self-inspection is restricted to deconstructable, simple, phenotypes. Furthermore, given Von Neumann's system, we know that via variation and selection, agents whose reproduction is by symbolic description, can evolve to explore the space of all possible complex phenotypes. The genetic symbol system, with its utilization of inert structures, opens up a whole new universe of behaviors and functionality which is not available to reproduction by self-inspection. In this sense, it can evolve phenotypes in an open-ended fashion: all describable (by the genetic code) proteins, and ensembles of proteins, can be produced and evolved.
Von Neumann clearly used the notion of description-based universal construction in a computer science context, where all construction must at some level be completely described or programmed. In his self-reproduction scheme a description encodes a complete blueprint of automata to be constructed by the universal constructor automaton. This need for a complete specification of self-reproducing automata is very far from the actual material machinery of genetic reproduction. So in what sense do we use the term description when speaking of the encoding of initial conditions (amino acid chains) in biological systems? Clearly, genes do not encode the complete specification of proteins and the means to produce them. That is, genes do not encode information such as how to fold a protein. All of this comes for free with the laws of matter and self-organization (Moreno et al, 1994). A true universal constructor, in a physical sense, would need to encode everything down to physical law. But as Pattee (1995a) argues, biological systems are physical systems which precisely gained control of the context-dependent rules of an environment, not of course the physical laws. They encode only those material aspects that can be controlled via specification of initial conditions.
When Von Neumann's universal constructor reads a description to construct some automaton, a semantic code is utilized to map (translate) instructions into computational actions to be performed. When the copier copies a description, only its syntactic aspects are replicated (transcription). Now, the language of this code presupposes a set of computational primitives for which the instructions are said to "stand for"(the semantics). In other words, descriptions depend on the set of computational primitives of the reading device (the constructor). If such a set of primitives is complete in the Turing sense, then it establishes a computationally universal language: any computable function can be described in the language. In contrast, in the material world, a construction code such as the genetic code presupposes a set of material building blocks that follow physical law. In this sense, material codes are not universal as they depend on material constituents which cannot be changed without altering the significance of the descriptions.
A material symbolic code is defined by a small, finite, number of symbols (e.g. codons in DNA), which can encode a finite number of primitive parts (e.g. amino acids). There is a countable number of functional structures which may be constructed with a given set of parts. From encoded messages, which we call representations (e.g. genes), a potentially infinite number of products can be constructed. This defines the representational capacity of a given MSS. The point is that, a particular MSS is tied to specific construction building blocks. The richer the parts, the smaller the required descriptions, but also the smaller the number of constructable products. Michael Conrad (1990) refers to this as a tradeoff between programmability and high evolutionary plasticity or efficient use of computational resources. Von Neumann referred to this as "the parts problem". He used simple building blocks such as "and" and "or" gates to build the code of his self-reproducing automata, which in turn required a 29 state cellular automata lattice and very complicated descriptions. Arbib (1966, 1967) was able to simplify von Neumann's model greatly by utilizing more complicated logical building blocks, but losing some generality.
A given set of parts such as amino acids, provides intrinsic dynamic richness which does not have to be specified by the symbol system on which construction commands are cast, making descriptions much smaller and establishing higher evolutionary plasticity. The cost of this plasticity or efficient ability to specify proteins, is that the genetic code is not universal in that it cannot specify anything whatsoever, but only those things that can be constructed from amino acid chains. It establishes nonetheless a MSS which can specify or describe any conceivable amino acid chain (with the amino acids used by the available tRNA molecules). This ability to describe and construct all possible initial condition arrangements of building blocks, means that the ability of a MSS to describe and construct any dynamic configuration is open-ended.
We should think of descriptions not as complete representations capable of producing universal specification, but rather as material representations that produce matter-specific dynamic configurations, that is, encoded initial conditions or constraints for material, developing, self-organizing systems. This is how Pattee sees descriptions in his semantic closure principle: the symbolic controls that impose material constraints. This view treats descriptions not as programs but as encoded initial conditions for self-organizing processes. As discussed in section 4, this inter-dependence between symbols and material constraints is completely ignored by cognitivist theories of physical symbol systems, but not by the biosemiotics framework or Pattee's semantic closure principle. Furthermore, the reproduction of self-organizing agents based on symbolic descriptions of initial conditions leads to an open-ended evolutionary process, as also discussed in section 4 and simulated in section 5.
When we talk of MSS, we naturally recall the physical symbol systems put forward by Newell and Simon (1976) (4).
"A physical symbol system consists of a set of entities, called symbols, which are physical patterns that occur as components of another type of entity called an expression (or symbol structure). Thus, a symbol structure is composed of a number of instances (or tokens) of symbols related in some physical way (such as one token being next to another). At any instant of time the system will contain a collection of these symbol structures. Besides these structures, the system also contains a collection of processes that operate on expressions to produce other expressions: processes of creation, modification, reproduction and destruction. A physical symbol system is a machine that produces through time an evolving collection of symbol structures." Newell and Simon (1976)
This definition of physical symbol systems adds nothing to the problem of the origin of representations and symbols nor to the empirical constraints of actual matter-symbol systems. In fact, it merely states the obvious: every symbol system, as any other thing, must follow physical laws. It does not specify the conditions in which matter may become symbolic, the constraints that matter and symbol may impose and require from one another, nor the conditions in which a semiotic model is necessary or preferable over or in addition to a physical one. Indeed, it does not even distinguish symbol from matter.
The Pattee/Von Neumann view of genetic information as descriptions of initial conditions, as outlined in section 3, is more reasonable that the Physical Symbol Systems hypothesis, because the symbolic and material aspects of evolving systems are clearly delineated and not blurred: symbolic descriptions represent initial conditions for the components of self-organizing agents. Let us now discuss in more detail this biosemiotics framework which is based on complementary informational and material modes of explanation.
Semiotics concerns the study of signs/symbols in three basic dimensions: syntactics (rule-based operations between signs within the sign system), semantics (relationship between signs and the world external to the sign system),and pragmatics (evaluation of the sign system regarding the goals of their users)(Morris, 1946). The importance of this triadic relationship of any sign system has been shown relevant for biology and genetics (e.g. Waddington, 1972; Pattee, 1982, 1995a; Cariani, 1998). Typically the semiotics of the genetic system is construed as follows: all processes taking place before translation (from transcription to RNA editing) define the set of syntactic operations; the relation between mRNA (signifier) and folded amino acid chains (signified), through the genetic code, implements a semantic relation; and finally, the selective pressures on the obtained proteins and their developed products as the pragmatic evaluation of the genetic sign system. More on the semiotics of the genetic system in (Rocha, 1998).
Semiotics leads us to think of symbols not simply as abstract memory tokens, but as material tools (Prem, 1998) used in the situated interaction between agents and their environments. The MSS used by evolving agents to reproduce (section 3), require the existence of encoded initial conditions of material building blocks that interact and self-organize with the laws of their environment. How a semiotic code between symbols and building blocks can arise from a material system is still very much a mystery both for biological and cognitive systems. In biology, interesting models of the origin of biological matter-symbol codes have been proposed (e.g. Bedian, 1982) or more recently (Nieselt-Struwe and Wills, 1997). In (Rocha and Hordijk, 2000) the emergence of symbolic activity in computer simulations of simple matter-symbol systems, and its relevance for Cognitive Science, is presented. Here I elaborate on the characteristics and requirements of MSS that lead to OEE. In section 5 results from simulations of these characteristics are presented.
When studying dynamically coherent agent-environment couplings it becomes hard to argue against the radical dynamicists claim that evolutionary systems, as situated agents, are best studied with nonrepresentational explanatory devices. Are we indeed better off abandoning the notion of representation and symbols altogether and adopting a purely dynamical view of the world, in which agents are just another indistinguishable dynamical component of a network of many components (Beer, 1995; Van Gelder and Port, 1995)?
The answer to the previous question depends on whether there are limitations to the current dynamical systems framework (Mitchell, 1998). More specifically, whether the reduction of evolving agents with semiotic codes to pure dynamical systems requiring nothing but a material or physical mode of description, turns out to be insufficient to explain natural phenomena. Physical law, which DST models, is not equipped to deal with concepts such as biological function, adaptation, and selection, which are the foundations of semantics. A dynamical systems model needs other tools to explain how a bird's wing functions both as an airfoil and an engine at the same time (Rosen, 1993), though it can clearly explain the possible dynamic configurations of the components of the wing. DST also does not allow us to "understand how two adaptive systems with very different dynamical portraits give rise to similar functional behavior, and understand the source of errors made by an adaptive system and how its function will be affected by various sorts of 'lesions'". (Mitchell, 1998)
The problem is that biological function is not an intrinsic property of physical law, but a selective property of populations of individuals evolving under natural selection. Natural selection can be described as a statistical bias on the rates of reproduction of populations of individuals. But this is as far as (statistical) dynamics can take us to describe this process. It can describe which components see their reproduction rates increase in population dynamics trajectories, but it cannot describe the adaptive strategies responsible for the increase. It cannot describe how a certain phenotypical characteristic of an organism gives it an advantage in a particular environment. For this type of context-dependent explanation we require, in addition to physical law, what Pattee (1995b) refers to as rules. Rules are context-dependent constraints which affect the behavior and success of agents in specific environments, and furthermore only make sense in these environments. For example, the rule "a layer of fat gives individuals a selective advantage", makes sense for certain animals in the arctic circle, but certainly not for equatorial ones. Such contingent constraints, in the discourse of Physics, exist as initial and boundary conditions.
In fact, what distinguishes biology from physics, is that biological organisms, subjected to natural selection, gained control of precisely those aspects of the environment which can be molded and which physical law does not describe. Obviously, living organisms obey physical law, but in addition to systems that merely follow physical law, they have gained control of context-dependent rules. In this sense, DST, qua physical law, cannot explain precisely those aspects that set living systems apart, and are therefore strictly biological.
"The reason that laws cannot describe [biological] function, is because we specifically restrict physical laws to describe only those properties of matter that are, by principles of invariance and symmetry, as independent of observers and individual measurements as possible. This is necessary to achieve the characteristic universality of laws. [...] In other words, only those universal and intrinsic aspects of matter that have no significance for individuals are described by laws, while those context-dependent, selective aspects of matter that have significance for individuals in a local environment are described by symbols. Of course, all symbols require material vehicles that obey all the laws, but symbolic function requires another model. These are complementary models, not dualism." (Pattee, 1995a, pages 14-15)
Since we need the ability to describe context-dependent function in evolutionary discourse, we need a complementary framework that includes both matter and semantics, such as biosemiotics. Furthermore, biological organisms gained control of context-dependent rules by creating genetic descriptions of initial conditions used to construct and self-organize their phenotype (5). Phenotypical development by self-organization is clearly a dynamically coherent process, which should therefore be modeled exclusively with the laws of matter. But, as discussed in section 3, genetic descriptions are dynamically incoherent with the self-organizing dynamics of evolving agents. To insist on a exclusive dynamical description of these essential components for OEE, is to completely miss their functional roles in the biological organization, which are informational and representational, not dynamic. Let us now discuss these roles in detail.
Symbols (e.g. codons in DNA) are the physical structures used to store representations (e.g. genes).Now, the role of representations is typically seen as the ability to participate in processes in lieu of actual components that they stand for. When features that are necessary are not present, they may "be represented; that is, something else can stand in for them, with the power to guide behavior in their stead. That which stands in for something else in this way is a representation; that which it stands in for is its content; and its standing in for that content is representing it." (Haugeland, 1991, page 62) Haugeland further requires that only those "stand-ins" which participate in a representational scheme are representations. Such a scheme requires that there exist several possible representation-content pairings, defined by an arbitrary code, and that there is a systematic syntax for producing, maintaining, and modifying representations.
The material representations of the genetic system (as well von Neumann's Self-Reproducing model), share some of these characteristics, but show a very important difference which becomes apparent when we distinguish between what representations are used for and useful for. Genetic descriptions are never used in a dynamical process in lieu of something else. Indeed, the necessity of considering some components of the living organization as symbols rather than matter, lies in their particular role of representations of initial conditions and not of dynamic players (section 3). Rather, via a code, symbols are used for constructing or specifying dynamic products. This is a reading and construction process, which in biology is referred to as translation and is implemented by the ribosome and tRNA molecules. Von Neumann referred to this role of genetic descriptions as the active role. In a biosemiotics framework, this is the semantic dimension of material representation: dynamically incoherent symbols are decoded to produce dynamic products. In this role, representations are used to produce and guide (constrain) dynamics, as Haugeland requires, but not by standing-in for anything, rather by being used to construct something.
Now, the material representations of the genetic system function in yet another role, Von Neumann's passive role of descriptions. In this role, descriptions are produced, manipulated, changed, and copied, but without any reference or recourse to their content. Semiotically, this role refers to the syntactic characteristics of material descriptions (Rocha, 2000): those operations which can be performed on representations independently of their content. Biological examples of these operations are the transcription of mRNA from DNA, RNA Editing processes (Rocha, 1995, 2000), and mutation and sexual recombination - the essential variation to achieve OEE through natural selection. In this role, representations also do not stand in for content and furthermore are not even used to produce or guide dynamics or behavior, but to disseminate existing or produce new representations. Because of this role, descriptions can be communicated and novelty created. This is what representations are useful for.
Ultimately, the value of representations is found when their content is expressed in an environment. The environmental ramifications of the encoded constructs, the phenotypes, are a result of their success in an environment. Semiotically, this is the pragmatic dimension of representations: the survival of the encoded dynamics. Nonetheless, OEE requires all the three dimensions of biosemiotics. Pragmatics denotes only the ultimate success of a given dynamic organism. As described above, semantics refers to the act of constructing a given dynamic configuration from the representations of its initial conditions, and syntax to the ability to communicate and create (by variation) new representations.
The three semiotic dimensions of material representations allow us to understand the unique and necessary role of symbols in the material living organization. Above we stressed that material representations are used for construction. Notice how this alone does not grant them a unique status in the living organization. Other arrangements could have been used for construction, such as the hypothetical self-inspection protein copier of section 3. Because different ways of constructing proteins are possible, the full-blown utility of MSS is a result of the passive role or representations, or if you will, their syntactic dimension: communication and variation (Rocha, 2000).
As seen in section 3, biological organisms are able to reproduce any conceivable phenotype built from a set of building blocks (the twenty amino acids of the genetic code), because they construct it from dynamically incoherent representations that are communicated (separately from the reading-construction machinery) to offspring. Without this ability to communicate passive representations, biological organisms would be restricted to simpler phenotypes: those with recoverable initial conditions (section 3.2). Furthermore, communication with variation, gives rise to construction of new phenotypes that can evolve via pragmatic selection.
In biological organisms, variation is applied solely to the syntactic representations. In fact, many different kinds of syntactic operations are observed in evolutionary systems, such as RNA Editing (Rocha, 1995; 1998). Variation is essential for OEE, but it needs to be paired with an encoding mechanism capable of expressing any conceivable phenotype. Clearly, a self-inspection system such as the hypothetical protein copier could evolve (in a Lamarckian way) with a variation mechanism applied to the proteins copied via self-inspection. But since the set of phenotypes achievable by self-inspection is smaller than those achievable by encoded construction (due to complex development), such variation would not lead to OEE. In section 5, a computational study is presented to better illustrate the evolutionary process of agents built from self-organizing building blocks via these two kinds of reproduction: MSS and self-inspection.
I have discussed the role of material representations in evolutionary systems, now I summarize these ideas in three requirements for MSS capable of OEE. The three requirements for MSS, project Pattee's semantic closure principle onto a biosemiotics setting, where we can rename it semiotic closure.
Requirement1: Dynamically Incoherent Syntax for Communication and Variation
MSS demand inert physical structures (arrangements of dynamic components) which can effectively be seen as dynamically incoherent regarding the overall machinery in which they are utilized as representations (section 3.1). The role of these physical structures is not defined by their dynamic characteristics but rather by their informational value. Let us refer to these structures as symbols. Symbols must have the ability to be manipulated and combined into new symbols. The set of possible symbol manipulations defines the syntax of the representations. Syntax is required for communication in reproduction and for variation, both essential for natural selection and OEE. Examples of inert structures are DNA and RNA, of material symbols are codons, and of representations are genes, or the pieces (phrases) of DNA that encode specific proteins.
Requirement 2: Semantics or Construction via Arbitrary Code
There needs to exist an arrangement of dynamic components to implement an arbitrary coding relation between the symbols of requirement 1, and initial conditions specifying arrangements of material building blocks which subsequently self-organize to produce some dynamic behavior - this is the semantic code (6). When we say that a symbolic description represents initial conditions, we mean that the (dynamically incoherent) first is used to construct the (dynamically coherent) second.
It is because of this code between symbols and initial conditions, that we need a complementary explanatory model which allows both dynamical and symbolic aspects - as Pattee has argued (e.g. Pattee, 1978). The dynamical dimension is used to explain the products of the encoding, while the symbolic dimension is used to explain the encoded representations. The biosemiotics framework offers such an explanatory device, leading us to think of the semantics implemented by a construction code as a material affair, rather than an abstract, surrogate relationship between internal and external elements. In this sense representations are conceptualized as something used to start off, not stand in for dynamic processes. Representations are used to, literally, materialize dynamical systems.
Requirement 3: The Complex Pragmatics of Development and Selection
The encoded initial conditions, after construction via the code of requirement 2, self-organize at different levels: the first products of the self-organization of building blocks specified by initial conditions (e.g. amino-acid chains), become themselves building blocks (e.g. proteins) for other self-organizing processes, and so on. After development of initial conditions, for evolution to occur, a feedback selection mechanism must exist to favor the sets of symbols representing the sets of initial conditions which produce successful dynamic behavior. This defines a selection criteria and the pragmatics of the representations. Since the process of development is typically not reversible, it is in most cases impossible to access the independent value, or pragmatic repercussions, of each participating representation (e.g. genes). Rather, feedback is applied to the entire set of representations a given agent possesses - agents as the unit of selection. In natural selection, this feedback is instantiated by increasing rates of reproduction of the more successful agents.
"We need simpler embodiments of natural matter-symbol systems with both empirical power and conceptual generality." (Pattee, 1982, page 327)
Howard Pattee pushed the study of matter-symbol systems from the cognitive to the biological and physical realms. His thesis has been that the matter-mind problem is too complicated to be approached initially at the cognitive level. By understanding the symbolic nature of genetics, he proposed, we may eventually be able to gain empirical and conceptual insight into the nature of more complicated mind-matter systems such as brains and culture.
However, his message has encountered some rejection or at least neglect even in the biological sciences. One reason for the lack of acceptance may be because it has been hard to distinguish between MSS based on representations used for construction, from the traditional view, from linguistics and cognitive science, of symbols, as "stand ins". Furthermore, the distinction between systems capable of OEE and those that evolve in more restricted ways is not obvious. In the prior sections, I have attempted a theoretical treatment of these distinctions, by thinking of MSS in terms of three biosemiotic requirements which can be used to bridge the notion of representation in cognitive and biological models. Below, I illustrate these issues with simulations of MSS.
Pattee (1989) has also articulated the notion that simulations of living organisms are not realizations. But simulations are capable of providing the kind of empirical power we need to study simpler matter-symbol systems. Indeed, the simplest known realization of a matter-symbol system, the cell, is still far too complicated to build the kind of empirical and conceptual generality he proposed. It could well be that before a "Cell Psychology" (Pattee, 1982) can be studied, we need an "Artificial Life Psychology". In (Rocha, 1998, 2000), a study of the origin of symbols from dynamical processes in Cellular Automata was pursued, while in (Rocha and Hordijk, 2000) these same systems were discussed as a means to study emergent representations in Cognitive Science. Here I present simulations of evolutionary processes with different reproduction strategies, to illustrate the advantages of MSS in evolutionary processes.
In the next subsections, the results of simulations of the evolution of agents is presented. The idea is to contrast the evolutionary potential of two different kinds of agents: those that reproduce by self-inspection and phenotypic variation, and those that reproduce by genetic description and genetic variation. Both types of agents posses identical phenotypes, whose self-organization from material building blocks is simulated. But whereas some agents reproduce their phenotypes directly by copying their building blocks (subjected to random variation of these building blocks), others reproduce by constructing from, and separately copying, descriptions of the initial conditions of these building blocks (subjected to random variation of descriptions). Figure 1 depicts both types of agents. The details of the agents, their environment, and the simulations performed follow.
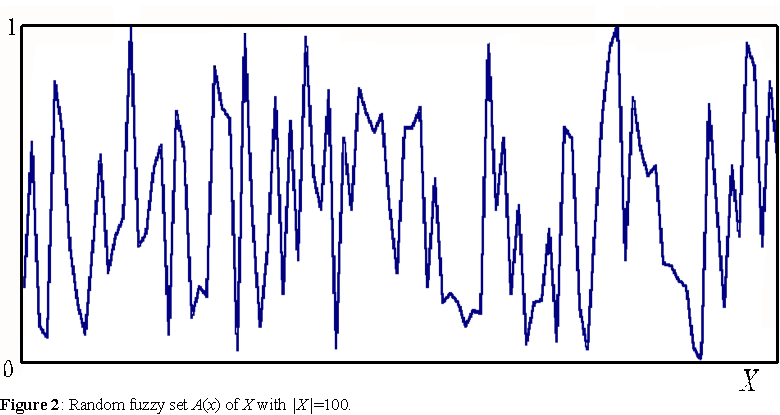
The most general artificial environment for simulations of evolving agents we can conceive, is defined by a set X of variables x. These variables refer to observables or attributes we wish to include and study in a given simulation - e.g. temperature, humidity, etc. To achieve generality, we want these values to take any possible numerical value. Thus, the state of an agent in the environment at a particular time is represented by a mapping from X to the real line. Fuzzy sets (Zadeh, 1965) are unconstrained mappings to the unit interval. A fuzzy set is able to capture the state of any agent whose attributes are defined by numerical values, since any real interval can be mapped to the unit interval. Given a universal set X containing all the variables x of an environment, a fuzzy set A, defined by the membership function A(x): X→ [0,1], represents a particular state of some agent in environment X (see figure 2).
For the purposes of simulations of evolutionary processes, we need to identify those agent states (defined by fuzzy sets) which are considered advantageous in the environment. Clearly, in the most realistic simulations of evolutionary systems, the fitness states are not a priori (explicitly) defined, but emergent (implicit) from the rates of reproduction of agents (e.g. Ackley and Littman, 1991; Werner and Dyer, 1991; Hutchins and Hazlehurst, 1991). But since the purpose here is to study simulations of reproduction strategies, not realistic agent-environment couplings, we can assume a fixed, explicit set of environmental demands or fitness function - as it is typically done in evolutionary machine learning and optimization (Goldberg, 1989).
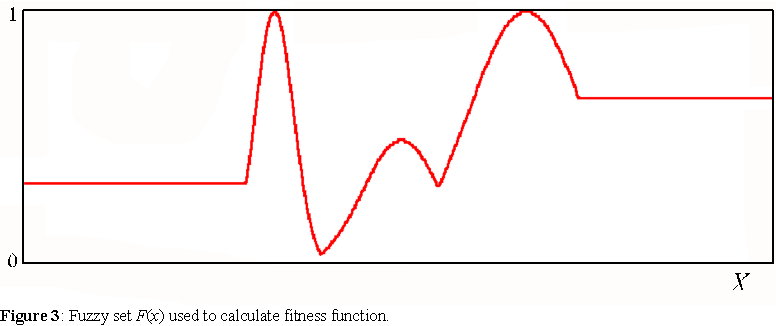
Thus, we can define the fitness of any agent A(x) in the generalized environment, as proportional to the Hamming distance from a particular desirable state, described by another fuzzy set F(x) of X. For this particular study, F is defined by the fuzzy union (maximum operator) of 2 constant and 3 exponential membership functions (see appendix A.1 for full details) as shown on figure 3. This choice of membership function is fairly arbitrary; it was designed so that it contains exponential functions with different spreads. Exponential functions were chosen because the agents used in the simulations described below, have access only to piece-wise linear functions to approximate F. We can think of this fuzzy set as the demands of the environment.
The fitness function of this environment is a fuzzy set function, fit (A), defined for all non empty fuzzy sets A(x) of X. This function takes integer values between 5 and 100. The highest value is achieved when the Hamming distance (see appendix A.2) between A(x) and F(x), divided by the cardinality of A(x), |A|, is smaller than 0.05. The lowest value is achieved when the Hamming distance between A(x) and F(x) is greatest (A). Between these limits, the fitness of a fuzzy set A(x) is:
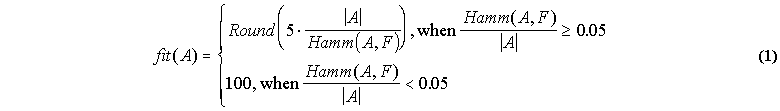
The agents we want to evolve in the environment of section 5.1 are defined by a particular fuzzy set A(x) of X, for which we can calculate a fitness value using equation 1. We can regard such a fuzzy set as the phenotype of a particular agent in environment X. Each agent produces its phenotype from a set of available building blocks according to a development scheme.
In sections 2, 3 and 4, it was emphasized that living
organisms are assembled from building blocks which then
self-organize to produce dynamic configurations. The
initial conditions of these building blocks are important for
this production of the dynamic compounds. That is, the
same building blocks in a different arrangement, self-organize or develop into different dynamic outcomes.
Therefore, just by analyzing the dynamic outcomes, one
cannot in general recover the exact initial arrangement of
building blocks. The development scheme used by the
agents here described models this complex behavior, but
we consider only one level of development, which should
be regarded as modeling the overall process of biological
development. When the building blocks of these agents are
combined to produce a final outcome, they are not
modeling specifically the folding of amino acid chains into
proteins, but rather a general multi-level development
process of self-organization (see section 3.2), in which the
initial arrangements of building blocks (the initial
conditions) are not recoverable, even though the sets of
building blocks (the components) employed are. Figure 4
depicts an abstraction of this process. The details of the
simulation of agent development from initial
configurations of building blocks into a particular fuzzy set of X follow.
Consider an initial fuzzy set A0(x) = 0.5 for all x of X, it is the
initial state of the phenotype of our agent A(x) in X. Consider
now a sequence of n fuzzy sets A1(x), A2(x), ... , An(x) which is
applied to A0(x) with the sequence of n fuzzy operations
O1, O2, ... , On, that is, A1 is applied to A0 with O1, A2 is then
applied with O2 to this result, and so forth. This sequence of n
fuzzy sets Ai(x) and operations Oi is a program to develop the
phenotype of agent A from state A0(x) to a final state A(x), a
fuzzy development program (FDP) of length n (Rocha, 1995, 1997):
A(x) = A0(x) O1 A1(x) O2 A2(x) On An(x). Notice that if some of
the operations Oi are non-commutative, then the sequence of
the FDP matters, that is, the permutations of the order of application of the FDP yield different final
states A(x). The building blocks of an FDP are the fuzzy sets and operations employed in the FDP
sequence, which now need to be specified.
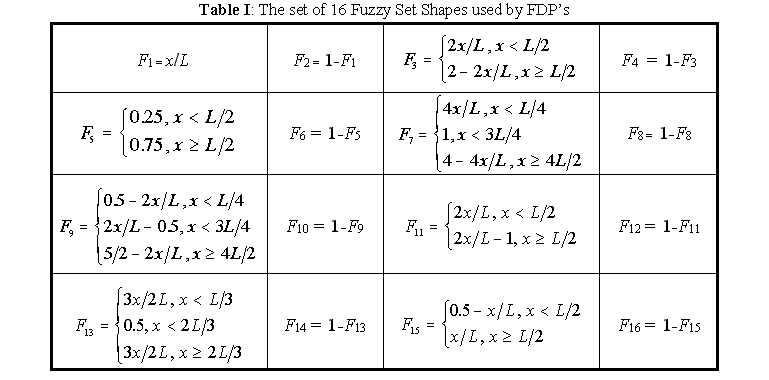
Consider a small set, F, of nF typical fuzzy set shapes (a few are depicted in figure 5). In the simulations here described 16 fuzzy set shapes were employed (nF = 16), specified by the following membership functions defined for all elements x of a generic interval of X , [0, L], as detailed in table I.
Consider also a small set, O, of nO fuzzy set operations. These operations range from commutative
operations such as fuzzy union (∪) and intersection (∩) to non-commutative operations such as
and 
, where the bar denotes fuzzy set complement (1-x). 16 distinct operations were used (nO
= 16): O1 =∪, O2 =∩, O3 = Avg, O4 = 1 - Avg, O5 =
, O6 =
, O7 =
, O8 =
,
O9 =
, O10 =
, O11 = A.B, O12 = 1 - A.B, O13 =
, O14 =
, O15 =
,
and O16 =
. All these operations are simple functions of two generic fuzzy sets A and B.
Operations 7, 8, 9,10, 13, 14, 15, and 16 are non-commutative, and are responsible for sequence-dependent FDP's.
Notice now that the fuzzy set shapes F of Table I are defined for a generic interval [0, L], and the operations O are applicable to any two generic fuzzy sets. This means that a FDP can be applied to any universal set X, whatever its size. To understand how this is done, we need to describe a few more parameters of FDP's.
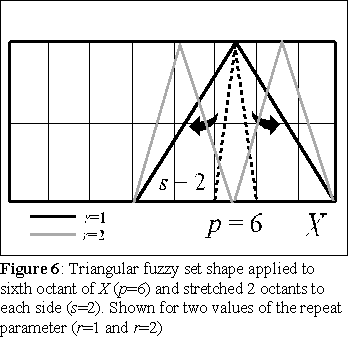Consider a partition of X in an even number nX of
parts. If nX = 8, X is divided in equal octants. In
addition to a specific shape Fi of F, each Ai(x) of an
FDP is associated with a specific part of
X: p = 1, ... nX. In other words, each shape Fi is applied
to part p of X with operation Oi. One other parameter
is s = 1, ... nX/2, which represents the number of parts
of X that shape Fi should be stretched over. Figure 6
shows the universal set X divided in octants (nX = 8),
and a triangular fuzzy shape, F3 (dotted line), being
applied to the sixth octant (p = 6) with a stretch of
two octants on each side of the sixth octant (s = 2). A
final parameter r = 1, ... nX/2 is defined which
represents the number of times shape Fi is going to be
repeated in the interval of X yielded by p and s. In
figure 6, the dark line represents r = 1, meaning that
the triangular shape is repeated once. When r is 2, the triangular shape is narrowed in half, and
repeated twice over the interval of X given by parts 4 to 8 (p=6, s=2), in figure 6 this is represented
by the gray line.
Given these parameters, the full specification of each fuzzy set/operation pair Ai/Oi of a FDP is given by the tuple (Fi , p, s, r, Oi), where Fi is a fuzzy set shape from F, p, s, and r the integer parameters described above, and Oi an operation from O. This tuple is referred to as a building block of an FDP.
FDP's define a scheme to construct an agent of environment X (section 5.1), defined by as many variables as desired, with a relatively small description. For details of the information requirements of FDP's see appendix A.3. The idea is that with a small Boolean description (a FDP), we can construct a fuzzy set of X, which is a real-valued structure. The ability to approximate any fuzzy set of X with a fuzzy set constructed via an FDP, is naturally dependent on the length (n) of the FDP's used and on the richness of its building blocks. The fuzzy set shapes of F used in the present work are all piece-wise linear, whereas the fitness function (equation 1) is built from exponential membership functions. Therefore, the agents of the simulations, which use FDP's to construct their phenotypes, approximate the fitness function with access only to linear building blocks. Figure 7 depicts a fuzzy set produced by a randomly generated FDP against the exponential fitness fuzzy set.
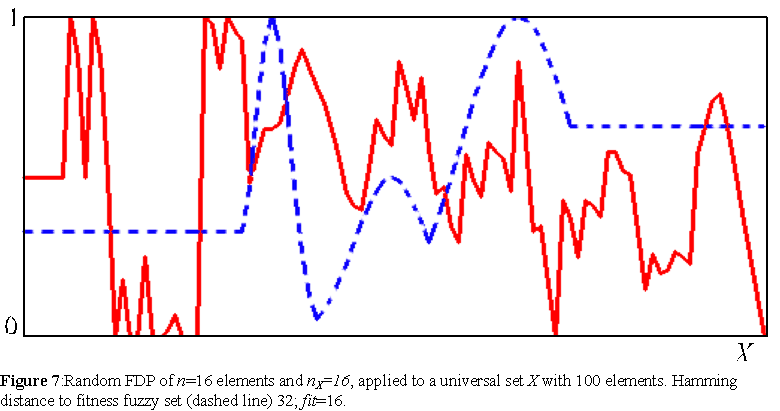
FDP's model the development of the phenotypes of agents from initial conditions: the sequence of building blocks. In this sense, FDP's model a material self-organization process, which is potentially irreversible due to the non-commutative operations employed in the FDP sequence. Furthermore, the final phenotype is the global outcome of the local assembly of linear fuzzy shapes applied to subsets of X. The FDP provides a scheme to integrate local contributions from subsets of X whose elements are linearly related according to fuzzy shapes from F. In this sense, the variables x of phenotypes produced by FDP's are not independent, but locally interdependent or epistatic. This can be seen by comparing the phenotype obtained from a random FDP (figure 7) with the completely random phenotype (figure 2). Though FDP's are not the typical constructs used to study self-organization, such as Cellular Automata, they model two important characteristics of development: irreversible arrangement of components and epistasis of phenotypic variables.
In this section we study the evolution of agents via direct reproduction (self-inspection) variation of their phenotypes. The idea is to study the evolutionary characteristics of agents that do not possess MSS to construct their phenotypes. To evolve, these agents also need to reproduce, be subjected to some kind of variation, and be selected according to the demands of an environment. Because these agents possess only phenotypes, they reproduce by self-inspection, in analogy to the "protein-world" discussed in section 3.2. Thus, when an FDP agent reproduces, the set of building blocks that produced its phenotype is accessible, but not the actual initial FDP sequence in which building blocks were arranged when the phenotype was produced. Therefore, reproduction in effect copies the set of building blocks, but rearranges them randomly into another FDP sequence which is then used to construct the phenotype of the offspring (figure 8).
For example, an agent whose phenotype fuzzy set was constructed with the following FDP with n=4 building blocks (applied to a universal set X with nX=16 partitions):
(F12, 3, 2, 4, O3) - (F5, 13, 1, 5, O9) - (F1, 6, 3, 1, O11) - (F15, 7, 8, 2, O4)
may reproduce an offspring whose phenotype is constructed with the following rearranged FDP:
(F15, 7, 8, 2, O4) - (F12, 3, 2, 4,O 3) -(F5, 13, 1, 5, O9) - (F1, 6, 3, 1, O11)
The phenotype, and resulting fitness, of the offspring maybe be quite different depending on whether the participating operations are commutative or not. Note that a compact way of representing these FDPs is as a string of hexadecimal characters where 0 denotes an index value of 1, and F an index value of 16. These two FDP's above can be represented respectively as B2132-4C048-0520A-E6713 and E6713-B2132-4C048-0520A. The hexadecimal notation is used form here on to describe evolved FDP's.
An evolutionary algorithm was performed on populations of agents generated with random FDP's (such as the one depicted in figure 7). Many different populations of agents were produced (with very similar results); here I describe the results of populations of 100 agents with FDP's of length n=16, |X|=100, and nX=16 (7). An elite evolutionary algorithm was employed (8):
Notice that in the case of FDP agents, the selection of agents into the elite does not exactly reproduce the FDP sequence. As described in the example above, the sequence of the FDP that produced a phenotype is lost, only its building blocks are recoverable. Therefore, the agents selected into the elite contain permutations of the FDP's of the agents with highest fitness in the original population.
The variation applied to FDP agents in step 4 is a kind of phenotypic crossover and mutation. Two agents of the elite are randomly selected (with repetition) as parents, m < n blocks of the FDP of one parent and n-m blocks of the FDP of the other parent are randomly chosen (without repetition) to produce the FDP of an offspring agent. A second offspring agent is produced with the remaining blocks from each parent. Thus, two parents produce two offspring by randomly combining the parents' FDP's. For instance, the two examples above may produce the following offspring:
(F1, 6, 3, 1, O11) - (F12, 3, 2, 4, O3) - (F12, 3, 2, 4, O3) - (F15, 7, 8, 2, O4)
(F5, 13, 1, 5, O9) - (F1, 6, 3, 1, O11) - (F5, 13, 1, 5, O9) - (F15, 7, 8, 2,O 4)
In addition to this phenotypic combination of building blocks, noise is applied to the building blocks of the FDP's of the offspring with probability pnoise. Noise means that (only) one of the parameters is changed in a block with this probability, e.g. (F12, 3, 2, 4, O3) → (F12, 16, 2, 4, O3).
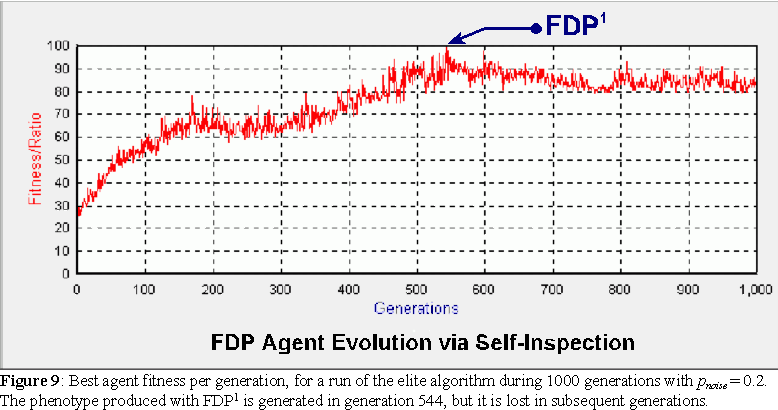
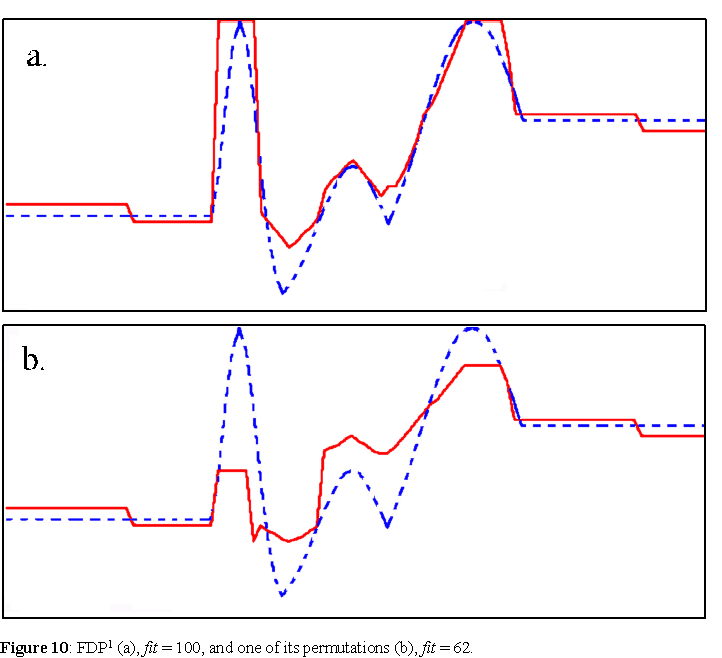
Unlike what happens with genetic algorithms, described in the next section, the evolution of FDP agents necessarily leads to greater variability, as the agents selected into the elite may not preserve the FDP's that produced phenotypes with high fitness. Often, a very fit agent is generated in one generation, but because of the self-inspection (direct) reproduction, its offspring's FDP may be different form the original and furthermore produce a worse phenotype in the subsequent generations, thus dropping out of the elite and the evolving population. A plot of such an evolutionary process is shown in figure 9. An agent with maximum fitness, constructed with FDP1, is produced on generation 544, but lost afterwards. If we analyze the FDP, we see that most operations used are non-commutative (denoted by bold italics): FDP1 = AB047 - 5503D - 47702 - 8B047 - E5027 - 87102 - 2B047 - AB037 - 49602 - 65027 - 55027 - 65027 - 09100 - AB027 - CB047 - 09100. Figure 10 shows a plot of FDP1 and one of its lower fitness permutations (first 3 blocks appended to the end).
Now, from an optimization perspective, the fact that these agents are lost in subsequent generations is irrelevant since we can store the best solution from every generation. Indeed, this algorithm produced on average agents with higher fitness than those produced with the genetic algorithm of the next section. The average fitness of 50 runs of 1000 generations with pnoise = 0.05, is 78.7, whereas for the genetic algorithm is 71.5. Several agents with maximum fitness, such as FDP1, were evolved in these runs, but were all lost in the subsequent generations. The fact that the evolutionary algorithm of FDP agents is able to produce good solutions, indeed, on average better than a genetic algorithm, is important for machine learning (Rocha, 1997). But here we want to contrast such a non-genetic, Lamarckian, evolutionary process via phenotypic self-inspection, with an evolutionary processes based on genetic or symbolic representations to appreciate the distinctions discussed in prior sections.
The FDP's that produce the phenotypes of the agents used in the evolutionary algorithm of section 5.3 can also be encoded in symbolic descriptions. That is, we can endow them with a genotype: basically a binary string (of length defined in appendix A.3) encoding each FDP. This second kind of agents possess a genotype that encodes an FDP, which then develops into a phenotype defined by a fuzzy set of X (as depicted in figure 1). In this sense, binary genotypes indirectly encode real-valued phenotypes. We can now use the same elite evolutionary algorithm of section 5.3, but with genetic transmission of descriptions from one generation to the next, and the traditional variation operations of genetic algorithms (GA): crossover and mutation of genetic bit strings (Goldberg, 1989). Crossover of two parents is based on the choice of a point in the middle of the genetic binary strings, with subsequent production of two offspring from the combination of the parents' binary strings to the left and right of this crossover point. Mutation is implemented by flipping the binary state of each bit in the binary string with probability pmut.
Like biological organisms, this second kind of agents reproduces by communicating to offspring descriptions of the initial conditions for developmental processes - the Von Neumann scheme instead of self-inspection (as the agents of section5.3). The MSS is modeled by the encoding from the binary strings of the genotype, to an FDP sequence of building blocks (the initial conditions). While the development from the fuzzy set building blocks is modeled by the (irreversible) FDP phenotype (Fuzzy Set) construction process. Genotypes can encode any conceivable FDP, and furthermore, they can reproduce its exact sequence to their offspring, thus always achieving the same phenotype (plus variation). In this sense, genotypes are inert structures that encode initial conditions for developing phenotypes, not phenotypes themselves. The advantage of using descriptions is the ability to bypass the irreversibility of developed phenotypes. Such irreversibility of development, as we saw in the case of the self-inspection agents of section 5.3, leads to the reproduction of offspring phenotypes distinct from parents and corresponding loss of very fit agents in the evolutionary process. In the next section, we evolve FDP agents that reproduce using descriptions, to demonstrate the bypass of the irreversibility of development, thus achieving more stable evolutionary processes capable of sustaining previous fitness gains.
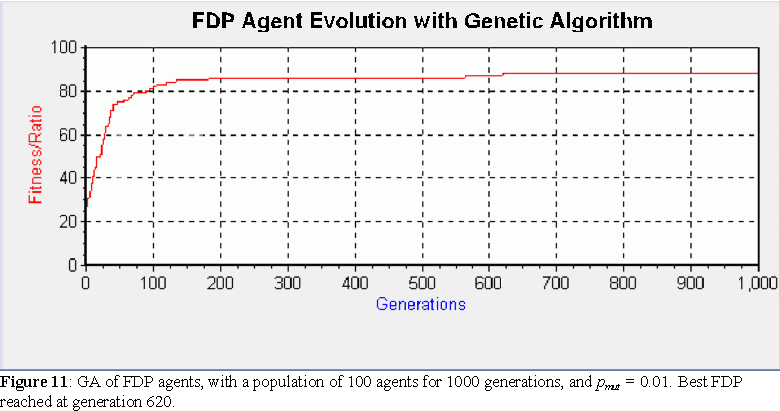
A typical run of the GA for FDP agents is shown in figure 11. As expected, the variability of the pure FDP agents disappears when we include genetic descriptions. Those agents that make it into the elite, are guaranteed the same FDP as their parents and therefore the same fitness. Notice, as mentioned in section 5.3, that the average fitness of the best agents obtained in the GA runs is actually lower than those obtained by the phenotypic variation algorithm of section 5.3. The best results were obtained with pmut = 0.01; the average fitness of the best agent in each run for a batch of 50 runs of 1000 generations was 71.5 (against 78.7 for the agents of section 5.3).
This difference might not be significant, but it shows that both algorithms are capable of reaching the same fitness levels, the issue is that the agents evolved by genetic variation, are better capable of transmitting their phenotypes to offspring than those produced by phenotypic variation. To appreciate better this distinction, the two types of agents were evolved in the same population of 100 agents; 50 of each kind. 50 runs of 1000 generations were performed for pmut=0.01 and pnoise=0.5 (9). In this algorithm, whenever agents of the two different types meet as parents to produce offspring, they simply reproduce themselves with mutation or noise (no crossover). When a pair of the same type is combined, the reproduction is as described in 5.3 and 5.4.
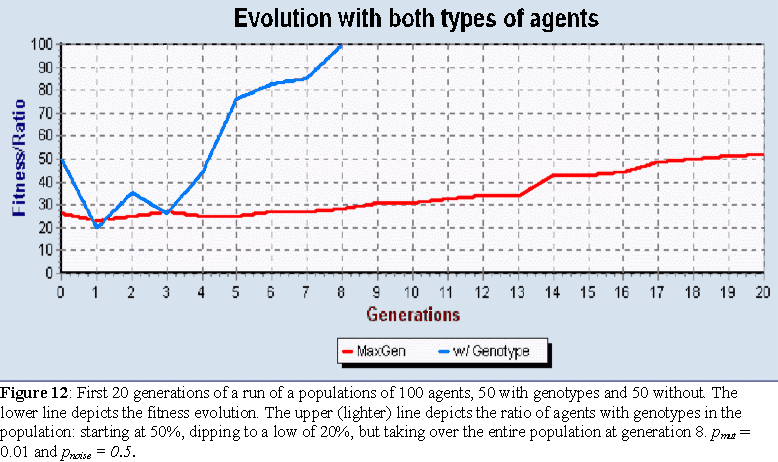
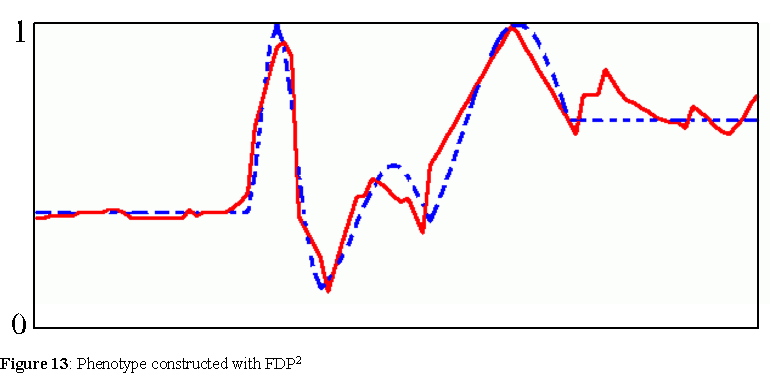
In every single run, the agents with genotypes took over the entire population, in an average of 4.3 generations. Figure 12 shows this drive towards a population of only agents with genotypes in one of these runs. In the elite algorithm, as soon as the elite contains agents of one type, the whole population is filled with this same type. 10 runs were tried with populations of 500 agents, but the average number of generations before the population became filled with agents with genotypes only slightly increased to 4.9. One of the best FDP's, with fit=100, was found in one of these runs with both types of agents, FDP2: 3C63A-FC525-96773-5E720-30308-BF702-D605F-42408-73502-8730E-97218-C5612-3C50C-49063-4B125-9C309. Figure 13 depicts the phenotype constructed with this FDP.
One thing we need to consider regarding these simulations, is if they are a result of the elite algorithm employed. Evolutionary algorithms, particularly the elite algorithm, are very idealized models of natural evolutionary processes, which do not include all of the real influences that occur in biological evolution. Clearly, the selection mechanism used in these simulations is very unrealistic. First, a fixed fitness function (eq. 1) is used to simplify the simulations. Second, the selection of the best agents in each generation into an elite subset establishes an all-or-nothing selection mechanism: only those that make it into the elite reproduce. Natural selection, on the other hand, is understood as a bias on the rates of reproduction of agents. Other evolutionary algorithms simulate this stochastic bias process more accurately. Instead of selecting an elite group of agents, the new population is constructed from a probabilistic roulette wheel which biases the selection of parents towards the agents with highest fitness (Goldberg, 1989). Furthermore, whereas in the elite algorithm the elite agents are not varied with crossover, mutation, or noise (only the remaining agents of the population built from them are), in this probabilistic algorithm, crossover occurs with a probability pcross for every set of two parents reproducing. With high values of this probability, all agents tend to be changed in the subsequent generation, thus potentially losing some of the advantage of keeping the best agents around.
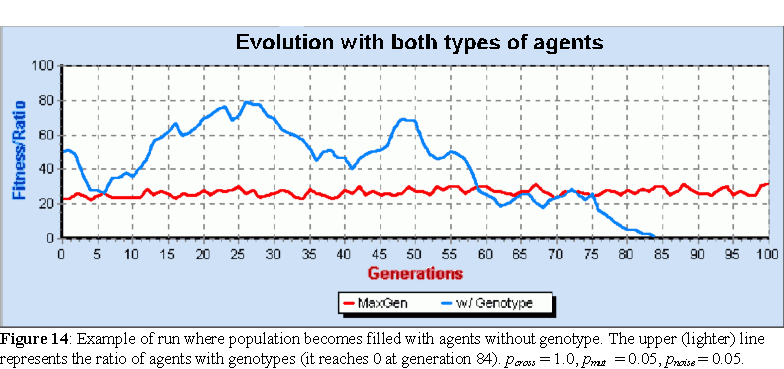
100 runs of this probabilistic evolutionary algorithm, with different values of pcross and the same values of pmut and pnoise used for the elite algorithm, were performed on populations of 100 agents, filled half and half with the two types of agents. The average fitness for the best agent at the end of 1000 generations in all these runs was 50.6, much lower than the 71.5 observed with the elite algorithm. Indeed, the fitness of the best agent discovered in all of these runs was only fit=64. However, the same behavior was observed when it came to the populations being taken over by agents with genotypes. For values of pcross < 0.7, all populations became entirely populated with agents with genotypes, in an average of 33.3 generations, much higher a value than the 4.3 observed with the elite algorithm. For values of pcross 0.7, about 90% of the populations became entirely populated with agents with genotype, but in about 10% of the runs, the population became entirely populated with agents without genotype (figure 14).
Clearly, as the value of pcross increases, all agents in the population tend to be crossed over when offspring are generated, which often results in the best agents in the previous generations being lost. In other words, as pcross increases, the advantage of the agents with genotypes is reduced as reproduction does not guarantee the same phenotype in the subsequent generation (10). Without some stability of the genetic representations used by agents, via an elite scheme or a lower crossover value, the advantage of agents evolved by variation and selection of symbolically encoded initial conditions for phenotypes dissipates. Indeed, if representations are not stable enough, we loose the necessary inertness of genetic descriptions of requirement 1 (section 4.3). But as long as this inertness is guaranteed, with a healthy amount of variation, agents with descriptions will take over the entire population. Therefore, these simulations show that in addition to the presence of irreversibility in a developmental process, description-based reproduction is advantageous only in the presence of some stability of descriptions as these are passed to offspring in the evolutionary process.
In this article I first presented arguments for why evolutionary systems use and benefit from using a MSS to encode initial conditions for arrangements of material building blocks that self-organize into phenotypes. The advantage put forward, based on the work of Von Neumann and Howard Pattee, is the ability to produce and reproduce any possible complex arrangement of the set of available building blocks (OEE), and not merely those simple ones that can be reproduced by self-inspection.
To illustrate this, I presented a simulation where two different kinds of agents, with and without symbolic descriptions, evolve; the first via phenotypic variation or (Lamarkian) self-inspection, and the second via genetic variation. Self-organizing processes were simulated with Fuzzy Development Problems, which implement a degree of irreversibility of developed phenotypes, based on a sequence of sometimes non-commutative operations. The agents without symbolic descriptions (genotypes), often reproduce different phenotypes than themselves because the original initial conditions that produced them are not entirely recoverable.
In contrast, the agents with genotypes can reproduce other agents exactly as themselves because they do not reproduce their phenotypes, but rather the genotypes containing the initial conditions that produce phenotypes. The simulations showed that even though the agents without genotypes are quite capable of producing very good solutions (on average better than the genotype ones), they cannot maintain them in the population as easily. Therefore, agents with genotypes eventually take over the entire population of agents. This shows how genetic descriptions offer both stabilizing and variation requirements for evolution. Stability because agents can reproduce the initial conditions to produce other agents such as themselves, and variation necessary to produce improvements. Without inert symbolic descriptions, the non-linear phenotypes of agents can evolve through variation, but do not as easily preserve the fittest agents. Finally, variation of descriptions needs to be low enough to guarantee some minimum stability of the fittest agents (section 5.6) - the inertness requirement.
Furthermore, notice that the agents endowed with genetic representations do not encode directly their phenotypes. To model MSS, these agents indirectly encode phenotypes by constructing them from encoded initial conditions and available building blocks. This indirect encoding models the material constraints of material symbol systems in the development of phenotypes via self-organization. Unlike traditional genetic algorithms, and the most radical theories of neo-Darwinian evolution, genetic descriptions do not directly represent particular traits of phenotypes. Rather, the final phenotypes are a result of non-linear self-organization, which is irreversible and produces epistatic dependencies on phenotypic traits. The agents of the simulations here presented, whose genotypes encode FDP's, possess these traits. The phenotypes produced are irreversible due to non-commutative operations, and the phenotype traits (the x variables) are epistatic, since they depend on multiple genotype locations.
This way, the present work shows that Pattee's arguments for the necessity of symbolic descriptions, for evolving agents to attain OEE, is valid only if their phenotypes are self-organized from material building blocks in a non-linear, irreversible, development process. Without this non-linear development stage, the advantage of symbolic descriptions would disappear, since agents that reproduce by self-inspection would have the same evolutionary potential, based on reproduction and variation of reconstructable, non-epistatic phenotypes. The advantage of symbols, thus, exists only when they are involved in a material coding relation with self-organizing building blocks: the symbol/matter interplay of the semiotic closure principle (section 4) (11). Hence, I offer the arguments of the present article, to stress that Pattee's drive to include semiotics in models of evolutionary systems, is not at all a dualist, but rather, a complementary materialist and semiotic position, which can furthermore be modeled computationally: there is no open-ended evolution without symbols, but conversely there is no need for symbols without material self-organization.
As Howard suggested from the study of simple matter-symbol interdependencies, such as the simulations here described, we are lead to re-think symbols themselves, as we reach the conclusion that representations are not substitutes standing for, but rather constructors of, material, evolving systems.
Ackley, D.H. and M. Littman [1991]."Interaction between learning and evolution." In: Artificial Life II. Langton et al (Eds). Addison-Wesley, pp. 487-509.
Arbib, M.A. [1966]."A simple self-reproducing universal automaton." Information and Control. Vol. 9, pp. 177-189.
Arbib, M.A. [1967]."Automata theory and development: Part I." Theoretical Biology. Vol. 14, pp. 131-156.
Bedian, V. [1982]."The possible role of assignment catalysts in the origin of the genetic code." Origins of Life. vol. 12, pp. 181.
Beer, R. [1995]."A dynamical systems perspective on agent-environment interaction." Artificial Intelligence. Vol. 72, pp. 173-15.
Cariani, Peter [1992]."Emergence and Artificial Life." In: Artificial Life II. C. Langton, C. Taylor, J.D. Farmer, and S. Rasmussen (eds.). SFI Series in the Sciences of Complexity. Addison-Wesley, pp. 775-797.
Cariani, Peter [1998]."Towards an evolutionary semiotics: the emergence of new sign-functions in organisms and devices ." In: Evolutionary Systems: Biological Perspectives on Selection and Self-Organization . G. Van de Vijver, S. Salthe, and M. Delpos (eds.). Kluwer, pp. 359-376.
Clark, Andy [1997]. Being There: Putting Brain, Body, and World Together Again . MIT Press.
Conrad, Michael [1990]."The geometry of evolutions." BioSystems. Vol. 24, pp.61-81.
Crick, F. [1968]."The origin of the genetic code." Journal of Molecular Biology. vol. 38, pp. 367-79.
Goldberg, D.E. [1989]. Genetic Algorithms in Search, Optimization, and Machine Learning. Addison-Wesley.
Goodwin, B. [1994]. How the Leopard Changed its Spots: The Evolution of Complexity. Charles Scribner's Sons.
Haugeland, John [1991]."Representational Genera." In: Philosophy and Connectionist Theory. w. Ramsey, S. P. Stich, D.E. Rumelhart (Eds.). Lawrence Erlbaum, pp.61-89.
Hoffmann, G.W. [1975]."The stochastic theory of the origin of the genetic code." In: Annual Reviews of Physical Chemistry. H. Eyring, C.J.Christianson, and H.S. Johnson (Eds.). Academic Press, Vol. 26, pp. 123-144.
Hoffmeyer, Jesper [2000]."Life and reference." Biosystems. This Volume. In Press.
Holland, J.H. [1995]. Hidden Order: How Adaptation Builds Complexity. Addison-Wesley.
Hutchins, E. and B. Hazlehurst [1991]."Learning in the cultural process." In: Artificial Life II. C. Langton, C. Taylor, J.D. Farmer, and S. Rasmussen. Santa Fe Institute studies in the sciences of complexity series. Addison-Wesley, pp. 689-706..
Kauffman, S. [1993]. The Origins of Order: Self-Organization and Selection in Evolution. Oxford university Press.
Klir, G.J. and B. Yuan [1995]. Fuzzy Sets and Fuzzy Logic: Theory and Applications. Prentice Hall.
Langton, C.G. [1986]."Studying Artificial Life with Cellular Automata." Physica D.. Vol. 22, pp. 120-149.
Maturana, H. and F. Varela [1987]. The Tree of Knowledge: The Biological Roots of Human Understanding. New Science Library.
Mitchell, Melanie [1996]. An Introduction to Genetic Algorithms. MIT Press.
Mitchell, Melanie [1998]."A complex-systems perspective on the 'Computation vs. Dynamics' debate in Cognitive Science." In: Proceedings of the Twentieth Annual Conference in Cognitive Science, COGSCI'98. M.A. Gernsbacher and S.J. Derry (eds.). pp. 710-715.
Moreno, A., A. Etxeberria, and J. Umerez [1994]."Universality without matter?." In: Artificial Life IV. R. Brooks and P. Maes (eds.). MIT Press, pp. 406-410.
Morris, C.W. [1946]. Signs, Language, and Behavior. G. Braziller Publishers..
Newell, A. and H. Simon [1976]."Computer Science as empirical inquiry: symbols and search." Communications of the ACM. Vol. 19, No.3, pp. 113126.
Nieselt-Struwe, K. and P.R. Wills [1997]."The emergence of genetic coding in physical systems." Journal of theoretical biology. Vol. 187, pp. 1-14.
Pattee, Howard H. [1961]. "On the origin of macromolecular sequences". Biophysical Journal. Vol. 1, pp. 683-709.
Pattee, Howard H. (Ed.) [1973]. Hierarchy Theory: The Challenge of Complex Systems. George Braziller, New York.
Pattee, Howard H. [1978]."The complementary principle in biological and social structures." Journal of Social and Biological Structures. Vol. 1, pp. 191-200.
Pattee, Howard H. [1982]."Cell psychology: an evolutionary approach to the symbol-matter problem." Cognition and Brain Theory. Vol. 5, no. 4, pp. 191-200.
Pattee, Howard H. [1989]."Simulations, realizations, and theories of life." In: Artificial Life. C. Langton (ed.). SFI Series in the Sciences of Complexity. Addison-Wesley, pp. 63-77.
Pattee, Howard H. [1995a]."Evolving self-reference: matter, symbols, and semantic closure." Communication and Cognition - Artificial Intelligence. Vol. 12, nos. 1-2, pp. 9-27.
Pattee, Howard H. [1995b]."Artificial life needs a real epistemology." In: Advances in Artificial Life. F. Moran, et al. Springer-Verlag. pp 23-38.
Pollack, R. [1994]. Signs of Life: The Language and Meanings of DNA. Houghton Mifflin.
Prem, Erich [1998]."Semiosis in embodied autonomous systems." In: Proceedings of the Joint Conference on the Science and Technology of Intelligent Systems '98. . IEEE Press, pp. 724-729.
Rocha, L.M. and W. Hordijk [2000]."Representations and Emergent Symbol Systems." Cognitive Science. Submitted.
Rocha, L. M. and Cliff Joslyn [1998]."Models of Embodied, Evolving, Semiosis in Artificial Environments." In: Proceedings of the Virtual Worlds and Simulation Conference. C. Landauer and K.L. Bellman (Eds.). The Society for Computer Simulation, pp. 233-238.
Rocha, Luis M. [1995]."Contextual genetic algorithms: evolving developmental rules." In: Advances in Artificial Life. J. Moran, A. Moreno, J.J. Merelo, and P. Chacon (Eds.). Springer -Verlag, pp. 368-382.
Rocha, Luis M. [1996]."Eigenbehavior and symbols." Systems Research. Vol. 13, No. 3, pp. 371-384.
Rocha, Luis M. [1997]. Evidence Sets and Contextual Genetic Algorithms: Exploring Uncertainty, Context and Embodiment in Cognitive and biological Systems. PhD. Dissertation. State University of New York at Binghamton.
Rocha, Luis M. [1998]."Selected self-organization and the Semiotics of Evolutionary Systems." In: Evolutionary Systems: Biological and Epistemological Perspectives on Selection and Self-Organization. S. Salthe, G. Van de Vijver, and M. Delpos (eds.). Kluwer Academic Publishers, pp. 341-358.
Rocha, Luis M. [2000]."Syntactic Autonomy: or why there is no autonomy without symbols and how self-organizing systems might evolve them." In: Closure: Emergent Organizations and Their Dynamics. J.L.R. Chandler and G. Van de Vijver (Eds.). Annals of the New York Academy of Sciences. Vol. 901, pp.207-223.
Rosen, Robert [1993]."Bionics revisited." In: The Machine as a Metaphor and Tool. H. Haken, A. Karlqvist, and U. Svedin (eds.). Springer-Verlag, pp. 87-100.
Salthe, Stanley N. [1993]. Development and Evolution: Complexity and Changes in Biology. MIT Press.
Umerez, Jon [1995]."Semantic Closure: a guiding notion to ground Artificial Life." In: Advances in Artificial Life. F. Moran, A. Moreno, J.J. Merelo, and P. Chacon (eds.). Springer-Verlag, pp. 77-94.
Van Gelder, T. and R. Port [1995]."It's about time: an overview of the dynamical approach to cognition." In: Mind as Motion: Explorations in the Dynamics of Cognition. R.Port and T. Van Gelder (Eds.). MIT Press, pp. 1-43.
von Neumann, J. [1955]. Mathematical Foundations of Quantum Mechanics. Princeton University Press.
von Neumann, J. [1966]. The Theory of Self-Reproducing Automata. University of Illinois Press.
Waddington, C.H. [1972]."Postcript." In: Towards a Theoretical Biology. C.H. Waddington (ed). Edinburgh University Press.
Werner, G.M. and M. G. Dyer [1991]."Evolution of Communication in Artificial Organisms." In: Artificial Life II. Langton et al (Eds). Addison-wesley, pp. 659-687.
Wheeler, Michael and Andy Clark [1999]."Genic representation: reconciling content and causal complexity." British Journal of Philosophy of Science. Vol. 50, pp. 103-135.
Wuensche, A. and M. Lesser [1992]. The Global Dynamics of Cellular Automata: An Atlas of Basin of Attraction Fields of One-Dimensional Cellular Automata. Santa Fe Institute Studies in the Sciences of Complexity, Addison-Wesley.
Zadeh, Lofti A. [1965]."Fuzzy Sets." Information and Control. Vol. 8, pp. 338-353.
Let f(x) be defined by the following exponential function applied to an interval [xi , xf] of X, of length L = xf - xi:
where xc is the interval's midpoint: xc = xi + L/2. α is a parameter that controls the spread of the exponential function. In this case, we want the function to be very close to zero (ε = 0.005)at the interval limits, so we define α as ln(0.005)/(L/2)
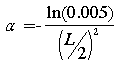
To construct the fuzzy set F used to calculate the fitness function, for a given universal set X, we construct 3 fuzzy sets using the exponential membership function f, applied to the intervals [1/4X, 5/12X], [5/12X, 11/12X], and [1/3X, 2/3X]: F1, F2, and F3 respectively. F3 is further multiplied by the constant ˝ so that it's peak is 0.5 rather than 1.0.
Two extra fuzzy sets are produced, F4 and F5, defined by step membership functions:
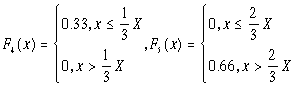
The union of two fuzzy sets is defined as the maximum operator on their membership function values. The set F is finally obtained by: F(x) = F1 (x) ∪ F2 (x) ∪ F3 (x) ∪F4 (x) ∪F5 (x) (see figure 3).
The Hamming distance between two fuzzy sets A1(x) and A2(x) is given by (Klir and Yuan, 1993):
Notice that the information required to specify an FDP, given F and O, does not depend on the size of X but on the parameters nX, nF, and nO, since we only need to identify the interval (p) of X where Fi is going to be stretched (s), repeated (r), and applied with operation Oi. We need only log2 nF and log2 nO bits of information to identify nF fuzzy set shapes and nO operations from F and O respectively. We further need log2 nX bits to describe the position p, and 2×log2 (nX/2) bits to describe the stretch s and repetition r. Therefore, log2 nF + log2 nX + 2×log2 (nX/2) + log2 nO bits are required to define each building block. In summary, a FDP requires the following bits of information to be described for any X:
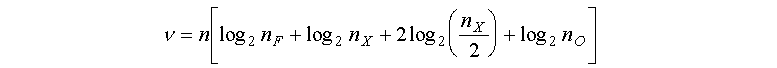
In the simulations here described, there are 16 possible fuzzy set shapes and 16 possible fuzzy logic operations, and X was divided in 16 parts. Thus, each building block in the FDP requires log2 16 + log2 16 + 2*log2 8 + log2 16 = 4 + 4 + 6 + 4 = 18 bits to be described. For FDP's of length n = 8 (16), 144 (288) bits are required. Notice that this value is independent of the cardinality of X.
FDP's define a scheme to construct an agent of environment X (section 5.1), defined by as many variables as desired, with a relatively small description. For the FDP's just detailed, if the cardinality of X is 100, we may be able to describe any agent with only 144 bits of information. Furthermore, notice that the variables x of X are defined by membership values on the unit interval, while the FDP description is binary (144 bits). In computational terms, real-type values usually require 4 to 10 bytes (32 to 80 bits) each. The computational description of a small number of elements of a fuzzy set easily surpasses the binary description of a FDP by several orders of magnitude. For example, 100 real type variables require 3200 to 8000 bits of information.
1. The three main abbreviations used throughout this article are MSS (Material Symbols Systems), OEE (Open-Ended Evolution), DST (Dynamical Systems Theory), and FDP (Fuzzy Development Programs).
2. Similarly to the argument here pursued, Hoffmeyer (2000) refers to dynamically coherent processes used to specify another dynamical system as analog codes, as opposed to dynamically incoherent digital codes such as the genetic system. I prefer to reserve the term code for dynamically incoherent representation schemes, which can be see as effectively symbolic as discussed in section 4.
3. Before developing his semantic closure principle, Pattee (1961) created models of structures capable of reproduction via self-inspection. The observation of the limitations of such models influenced very much the development of his semantic closure principle.
4. Newell and Simon defined physical systems in the context of their Physical Symbol System Hypothesis, which states that any physical symbol system (of sufficient size) will have the ability to exhibit intelligent behavior, and, furthermore, that any system that exhibits intelligent behavior necessarily has to be a physical symbol system.
5. According to Pattee, what distinguishes living from non-living matter is precisely the ability to select distinct initial conditions.
6. To say "arbitrary code" is actually redundant, since arbitrariness is a condition for having a code to begin with (Umerez, 1995). The point is that the content of the (symbolic) representations does not depend on their physical characteristics. There is no known reason to disclaim the idea that the current genetic code could have been set up differently, that is, with different RNA codon - amino acid relations defined by tRNA molecules (Crick, 1968; Hoffmann, 1975).
7. The software developed to implement all the evolutionary algorithms here described, the generation of FDP's, as well as data for runs with other parameters are available online.
8. For an overview of different types of evolutionary algorithms, including variations of the elite scheme, please refer to (Mitchell, 1996).
9. Other values were tested, but these values of mutation and noise yielded the best results when the two types of agents were evolved independently as described above.
10. Notice that the way the crossover operation is implemented in these evolutionary algorithms, as a mechanism for variation of successful solutions (Holland, 1995), is clearly not a realistic model of sexual reproduction. Crossover should be seen merely as an abstract mechanism for variation of genetic descriptions.
11. Notice however that this material involvement is dynamically incoherent (non-reactive). As discussed in section 3, the components we regard as symbols do not participate dynamically (chemically) in the self-organization process of the encoded building blocks. Rather, they participate as information carriers which are effectively read to construct initial conditions for self-organization.
