Selected Self-Organization and the Semiotics of Evolutionary Systems

Abstract: In this paper I sketch a rough taxonomy of self-organization which may be of relevance in the study of cognitive and biological systems. I frame the problem both in terms of the language of second- order cybernetics as well as the language of current theories of self-organization and complexity. The goal of establishing such a taxonomy is to allow for a classification of different tools used both in Artificial Intelligence and Artificial Life, so that different aspects of cognitive and biological systems may be incorporated in more accurate models of such systems. In particular, I defend, on the one hand, that self-organization alone is not rich enough for our intended simulations, and on the other, that genetic selection in biology and symbolic representation in cognitive science alone leave out the very important (self-organizing) characteristics of particular embodiments of evolving and learning systems.

Keywords: Self-organization, Semantic Closure, Semiotics, Emergence, Evolutionary Strategies, Artificial Life, Artificial Intelligence.

1 Eigenbehavior and Emergent Representation

Heinz von Foerster [1965, 1969, 1977] equated the ability of an organization to classify its environment with the notion of eigenbehavior. He postulated the existence of some stable structures (eigenvalues) which are maintained in the operations of an organization's dynamics. Following Piaget [von Foerster, 1977], he observed that any specific instance of observation of such an organization, will still be the result of an indefinite succession of cognitive/sensory-motor operations. This reiterated the constructivist position that observables do not refer directly to real world objects, but are instead the result of an infinite cascade of cognitive and sensory-motor operations in some environment/subject coupling. Eigenvalues are self-defining, or self-referent, through the imbedding dynamics _ implying a complementary relationship (circularity, closure) between eigenvalues and cognitive/sensory-motor operators: one implies, or defines, the other. "Eigenvalues represent the externally observable manifestations of the (introspectively accessible) cognitive [operations]". [von Foerster, 1977, page 278, italics added]. Further, "Ontologically, Eigenvalues and objects, and likewise, ontogenetically, stable behavior and the manifestation of a subject's 'grasp' of an object cannot be distinguished." [von Foerster, 1977, page 280]. Eigenbehavior is thus used to define the behavior of autonomous, cognitive systems, which through the closure (self-referential recursion) of the sensory-motor interactions in their nervous systems, give rise to perceptual regularities as objects [Varela, 1979, chapter 13].

"Eigenvalues are discrete (even if the domain of [their observables] is continuous)". In other words, even if the domain of an observable is continuous, its cognitive representation through cognitive/sensory-motor operators into eigenvalues must be discrete. This is a result of the stability of eigenvalues in the recursive chain of cognitive operators, if an eigenvalue changes its structure, thus ending the frame of stability, it will either revert to unstable structures (varying at each cognitive operation), in which case the eigenvalue representation is lost, or form another frame of stability with a new eigenvalue representation. Insummary, eigenvalues are discrete representations of observables maintained by the successive cognitive operations of a cognitive agent. Notice that the representations and their stability are specific to the particular cognitive operations and how they recognize observables, that is, these discrete representations exist only in relation to the very same operators that define them. Any system, cognitive or biological, which is able to relate internally, self-organized, stable structures (eigenvalues) to constant aspects of its own interaction with an environment can be said to observe eigenbehavior. Such systems are defined as organizationally closed because their stable internal states can only defined in terms of the overall dynamic structure that supports them. Organizationally closed systems are also informationally open [Pask, 1992], since they have the ability to classify their constructed environment in what might be referred to as emergent representation.

1.1 Attractor behavior, self-organization, and constructivism

An eigenvalue of an organizationally closed system can be seen as an attractor of a self-organizing dynamical system. The global "cooperation" of the elements of a dynamical system which spontaneously emerges when an attractor state is reached is understood as self-organization [von Foerster, 1960; Haken, 1977; Prigogine, 1985; Forrest, 1991; Kauffman, 1993]. The attractor behavior of any dynamical system is dependent on the structural operations of the latter, e.g. the set of boolean functions in a boolean network. Speaking of an attractor makes sense only in relation to its dynamical system, likewise, the attractor landscape defines its corresponding dynamical system. Further, attractor values can be used to refer to observables accessible to the dynamical system in its environment and therefore perform relevant classifications in such environment (e.g. neural networks). Naturally, and this is the crux of the constructivist position in the theory of organizationally closed systems, not all possible distinctions in some environment can be "grasped" by the autonomous system: it can only classify those aspects of its environment/sensory-motor/cognitive interaction which result in the maintenance of some internally stable state or attractor (eigenvalue). In other words, not everything "out there" is accessible; only those things that a particular physiology can construct with the stabilities of its own dynamics are. As with eigenvalues, attractors must be discrete even if used to refer to continuous observables.

1.2 Emergence and levels of description

There are three levels that need to be addressed when dealing with the notion of emergent representation. First, there is the material, dynamical, substrate, which will be the causal basis for all other levels that we may further distinguish. Secondly, we have the attractor behavior of this dynamics. Finally, we have the utilization of the set of attractors (eigenvalues) as referents for some aspects of the interaction of the dynamical system itself with its environment, that is, as tokens for eigenbehavior. This indirect, constructed, "referring" results from the structural coupling [Maturana and Varela, 1987] of the dynamical system with the environment, and can be understood as a semantic relation.

The level of eigenvalues is emergent to the dynamics because it cannot be explained solely by a description of the latter. Stability of dynamical states is not expressed in the language of the interactions between the components of a dynamical system. At this lower level, there is no distinction between a stable and an unstable state. For instance, the transition rules of Conway's game of Life cannot describe what "blinkers" and "gliders" are. Likewise, the level of eigenbehaviors, or the function of attractors as referring to some constructed reality, is emergent to the eigenvalues since the latter can only describe stabilities of the dynamics and not any "standing for" relation necessary for eigenbehavior (e.g. streams of gliders as information carriers in a universal computer built out of Life patterns [Poundstone, 1987]). No physical or formal description of the dynamical system and its attractors alone will completely explainthis functional dimension [see Rocha, 1994a, 1995b; Rosen, 1995; Pattee, 1995]. Hence, we need complementary descriptions of the several levels involved in such organizationally closed, emergent, systems [Pattee, 1978].

2 Embodiment and self-organization

Varela, Thompson, and Rosch [1991] have proposed an embodied, inclusive, approach to cognition which acknowledges the different levels of description necessary to effectively deal with emergent representation, or in von Foerster's terms, eigenbehavior. Cognitive science used to be traditionally concerned solely with those aspects of cognitive representation which can be described as symbolic. In other words, it was concerned with the semantic relation between cognitive categories and their environmental counterparts through some direct representational relation (intentionalty), without taking into account any sort of material or internal organizational constraints: real-world categories directly represented by discrete symbols which could be freely manipulated. The connectionist, emergent, or self- organizing paradigm has changed this focus to the lower level of attractor behavior. That is, cognitive systems are defined as those systems capable of self-organizing their components into discrete basins of attraction used to discriminate the environment they are able to construct. Classifications become subsymbolic and reside in some stable pattern of activation of the dynamic system's components, instead of based on some higher level symbols (emergent representation).

2.1 Selected Self-organization: structural change and increasing variety

What is usually referred to as self-organization is the spontaneous formation of well organized structures, patterns, or behaviors, from random initial conditions. The systems used to study this phenomenon are referred to as dynamical systems: state-determined systems. They possess a large number of elements or variables, and thus very large state spaces. However, when started with some initial conditions they tend to converge to small areas of this space (attractor basins) which can be interpreted as a form of self- organization. Since such formal dynamical systems are usually used to model real dynamical systems such as chemical networks of reactions, non-equilibrium thermodynamic behavior [Nicolis and Prigogine, 1977] the conclusion is that in nature, there is a tendency for spontaneous self-organization which is therefore universal [Kauffman, 1993].

This process of self-organization is also often interpreted as the evolution of order from a disordered start. Self-organizing approaches to life (biological or cognitive), in particular second-order cybernetics [see Pask, 1992], take chaotic attractors as the mechanism which will be able to increase the variety (physiological or conceptual) of organizationally closed systems. External random perturbations will lead to internal chaotic state changes; the richness of strange attractors is converted to a wide variety of discriminative power. Dynamic systems such as boolean networks clearly have the ability to discriminate inputs. Generally, the attractors of their dynamics are used to represent events in their environments: depending on inputs, the network will converge to different attractors. However, for any classification to have survival value, it must relate its own constructed states (attractors) to relevant events in its environment, thus, similar events in the world should correspond to the same attractor basin. Chaotic systems clearly do not have this property due to their sensitivity to initial conditions. Ordered systems follow this basic heuristic.

Kauffman [1993, page 232] further hypothesizes that "living systems exist in the [ordered] regime near the edge of chaos, and natural selection achieves and sustains such a poised state". This hypothesis is based on Packard's [1988] work showing that when natural selection algorithms are applied to dynamic systems, with the goal of achieving higher discriminative power, the parameters are changed generally tolead these systems into this transitional area between order and chaos. This idea is very intuitive, since chaotic dynamical systems are too sensitive to parameter changes, that is, a single mutation leads the system into another completely different behavior (sensitive to damage). By contrast, ordered systems are more resilient to damage, and a small parameter change will usually result in a small behavior change which is ideal for smooth adaptation (hill-climbing) in correlated fitness landscapes. However, even though very ordered systems can adapt by accumulation of useful successful variations (because damage does not propagate widely), they may not be able 'step out' of certain areas of their fitness landscapes. It is here that systems at the edge of chaos enter the scene; they are not as sensitive to damage as chaotic systems, but still they are more sensitive than fully ordered systems, and thus, some mutations will accumulate (by causing minor changes) and some others will cause major changes in the dynamics allowing more distant searches in fitness spaces. These characteristics of simultaneous mutation buffering (to small changes) and dramatic alteration of behavior (in response to larger changes) is ideal for evolvability [Conrad, 1983, 1990].

Chaotic classifications cannot grasp an ordered interaction with an environment, while point attractors and simple limit cycles may not allow enough behavior change for a good increase in variety. The edge of chaos regime seems to offer a good, intuitive, compromise. However, whatever the regime of a dynamic system, self-organization alone cannot escape its own attractor behavior. A given dynamic system is always bound to the complexity its attractor landscape allows. For a dynamic system to observe genuine emergence of new classifications (conceptual or of functionality) it must change its structure. Creativity, or open-ended variety can only be attained by structural perturbation of a dynamical system. One way or another, this structural change leading to efficient classification (not just random change), has only been achieved through some external influence on the self-organizing system. Artificial neural networks discriminate by changing the structure of their connections through an external learning procedure. Evolutionary strategies rely on internal random variation (mutation) which must ultimately be externally selected. In other words, the self-organizing system must be structurally coupled to some external system which acts on structural changes of the first and induces some form of explicit or implicit selection of its dynamic representations: selected self-organization.

2.2 Memory and selected self-organization

The dynamical approach of von Foerster [1965] to cognition emphasized the concept of memory without a record. By utilizing functionals to change the functions of state-determined systems, von Foerster formalized the idea that memory can be observed in systems which are able to change their own structure and therefore its dynamics and attractor behavior. Today, we name this kind of memory distributed, and the kind of models of memory so attained as connectionist. As previously discussed, for a self-organizing system to be informationally open, that is, for it to be able to classify its own interaction with an environment, it must be able to change its structure, and subsequently its attractor basins, explicitly or implicitly. Explicit control of its structure would amount to a choice of a particular dynamics for a certain task (the functional would be under direct control of the self-organizing system) and can be referred to as learning. Under implicit control, the self-organizing system is subjected to some variation of its structure (including its distributed memory) which may or may not be good enough to perform our task. Those self-organizing systems which are able to perform the task are thus externally selected by the environment to which they are structurally coupled. If reproduction is added to the list of tasks these systems can produce based on their dynamic memories, then we have the ingredients for natural selection: heritable variation and selection.

This form of situated, embodied, self-organization can be referred to as distributed memory selected self- organization. Its relying on some system-environment coupling of structure has been stressed mostnotably within second-order cybernetics and systems research. Maturana and Varela [1987] propose structural coupling as the general mechanism for variety increase, Pask [1976] refers to it as conversation in the cognitive realm. Both of these approaches owe a lot to von Foerster's eigenbehavior notions. More recently, in the realm of complex systems and evolutionary systems theory, Kauffman [1993] and others have relied on the notion of autocatalytic sets which are mutable, heritable, self-replicating, self- organizing systems evolvable through natural selection.

So far I have maintained that eigenvalues or attractors represent the building blocks of any system capable of discriminating its environment through some thus embodied construction. However, eigenbehavior (emergent representation) and its variety increase needs a structural coupling of these eigenvalues with some externally selective environment. This kind of selected self-organization obliges us "to understand perception not just as an interactive dynamical structure, but as a process that arises from a more fundamental embodiment that makes it possible for evolution to create structures that are internally assigned interactive roles. This process carries with it an increase of complexity of the way the environment is perceived and acted upon" [Etxeberria, 1995]. It also seems to offer a minimum requirement for evolution and cognitive categorization [Lakoff, 1987; Rocha, 1995d].

Perhaps the most important characteristic of this distributed memory selected self-organization is the fact that its specific embodiment both constructs the classification of the environment and ultimately defines selection. The consequence of this fact for biological systems is that natural selection (acting on this form of self-organization) is not free to evolve any organism, but it is constrained by the self-organizing properties of the materiality of the organisms it acts upon _ evolution with both a self-organizing and selection component. The consequence for cognitive systems, is that what can be classified is also constrained by the particular materiality of the classifying system at stake _ not everything "out there" can be grasped. In other words, the particular self-organizing dynamics of a particular classifying system constrains the universality of its classification. However, we should look into how can this process be made more efficient, and allow for genuine open-ended emergence of variety in classification.

3 Von Neumann: description based selected evolution

Von Neumann [1966] defended that a threshold of complexity exists, before which complexity degenerates, and after which complexity can increase in an open-ended fashion. He proposed a self-replicating scheme based on the notion of a memory-stored description Φ(A) that can be interpreted by auniversal constructor A to produce A itself. However, to avoid a logical paradox of self-reference, the description, which cannot describe itself, must be both copied (uninterpreted role) and translated (interpreted role ) into the described automaton. This way, in addition to the universal constructor, an automaton B capable of copying any description, Φ, is included in the self-replication scheme. A third automaton C is also included to effect all the manipulation of descriptions necessary. To sum it up, the self-replicating system contains the set of automata (A + B + C) and a description Φ(A + B + C); the description is fed to B which copies it and to A which constructs another automaton (A + B + C); the copy is then handled separately to the new automaton which together with this description is also able to self- reproduce.

3.1 Descriptions and open-ended evolution

As Von Neumann [1966] discussed, if the description of the self-reproducing automata is changed (mutated), in a way as to not affect the basic functioning of (A + B + C) then, the new automaton (A + B + C)' will be slightly different from its parent. Von Neumann used a new automaton D to be included in the self-replicating organism, whose function does not disturb the basic performance of (A + B + C); ifthere is a mutation in the D part of the description, say D', then the system (A + B + C + D) + Φ(A + B + C + D') will produce (A + B + C + D') + Φ(A + B + C + D'). Von Neumann [1966, page 86] further proposed that non-trivial self-reproduction should include this "ability to undergo inheritable mutations as well as the ability to make another organism like the original", to distinguish it from "naive" self- reproduction like growing crystals. Von Neumann's model clearly does not rely on a distributed but on a local kind of memory. Descriptions entail a symbol system on which construction commands are cast. These commands are not distributed over patterns of activation of the components of a dynamic system, but instead localized on "inert" structures which can be used at any time _ a sort of random access memory. By "inert" I mean material structures with many dynamically equivalent states, in other words, the semantic relation, or what the structures are used to refer to, must possess a large degree of arbitrariness so that certain representations are not much more probable than others. In the genetic system, any sequence of nucleotides is possible, and its informational value is not dependent on the particular attractor behavior of DNA or RNA dynamics.

Why then is there an advantage of local memory over distributed memory self-replication? Von Neumann's argument mainatins that if we do not have symbolic descriptions directing self-replication, then an organism must replicate through material self-inspection of its parts. In other words, the dynamics must be able to produce copies of itself by template identification of parts existing in its environment. The simplest way would be to have every part of the structure individually heritable. Clearly, as systems grow in complexity, self-inspection becomes more and more difficult [Pattee, 1995]. The existence of a language, a symbol system, allows a much more sophisticated form of communication. Functional, dynamic structures do not need to replicate themselves, they are simply constructed from physically non- functional (dynamically inert) descriptions. For instance, for an enzyme to replicate itself, it would need to have this intrinsic property of self-replication "by default", or it would have to be able to assemble itself from a pool of existing parts, but for this, it would have to "unfold" so that its internal parts could be reconstituted for the copy to be produced [Pattee, 1995]. With the genetic code, however, none of these complicated "gimmicks" are necessary: functional molecules can be simply folded from inert messages. This method is by far more general since any functional molecule (with limitations to be discussed ahead) can be produced from a description, not merely those that either happen to be able to self-reproduce, or those that can unfold and fold at will to be reproduced from available parts. The evolution of distributed memory based self-organizing systems is restricted to this type of trivial (in von Neumann's sense) or through self-inspection (self-description [Kampis, 1991]) reproduction.

The symbol system, with its utilization of inert structures, opens up a whole new universe of functionality which is not available for purely dynamical self-replication. In this sense, it can evolve functions in an open-ended fashion. The threshold of complexity proposed by Von Neumann is taken by some (e.g. Pattee, Cariani, Kampis in Rocha [1995a]) as another category of self-organization which is capable of creative organization and selection from outside. Following our rationale above, we can call it local memory selected self-organization, or description based selected self-organization. In biology, this means that living systems can follow a largely open-ended evolutionary history (von Neumann;s threshold of complexity). In the cognitive realm, the introduction of symbols also opened up a whole new world of communication possibilities as the aspects of an environment that can be communicated between individuals is not restricted to only those things we can "show" or otherwise somehow physically mimic: the displacement of local observations.

3.2 Semantic Closure: open-endedness, materiality, and universality

The notion of description implies a self-referential linguistic mechanism. A description must be cast on some symbol system while it must also be implemented on some physical structure. Since manyrealizations of the same symbol system are possible, viewing descriptions only as physical systems explains nothing about their symbolic nature in the control of construction. When A interprets a description to construct some automaton, a semantic code is utilized to map instructions into physical actions to be performed. When B copies a description, only its syntactic aspects are replicated. Now, the language of this semantic code presupposes a set of material primitives (e.g. parts and processes) for which the instructions are said to "stand for". In other words, descriptions are not universal as they refer to some material constituents which cannot be changed without altering the significance of the descriptions. We can see that a self-reproducing organism following this scheme is an entanglement of symbolic controls and material constraints which is closed on its semantics. Howard Pattee [1982, 1995] calls such a principle of self-organization semantic closure.

It is important to understand that when we say that a description based selected self-organizing system is endowed with open-ended evolutionary potential we do not believe it is universal, that is, that any physical system can be evolved. A given semantically closed system is based on some sort of coding mechanism between inert and functional structures. However, the code and the associated construction are built on some material substrate constraining the whole semantic closure: there is a finite number of functional structures which may be constructed with a given set of parts. The degree of open-endedness will be dependent on the representational potential of this code. In other words, the larger the number of possible equally dynamically inert structures, the larger the universe of functionality that can be represented in them. For instance, living systems cannot evolve any functional structure whatsoever (we have never seen animals on wheels for instance), but still the number of possible functional combinations attainable with the DNA-protein code system is very large, far beyond computational limits. In this sense, the emergence of functionality is open-ended [Cariani, 1989, 1993] though not universal.

It is here that the emphasis on the symbolic level of open-ended evolutionary systems must be tamed. Strong Darwinism, has emphasized the nature of the symbolic description of living systems, as much as strong cognitivism has emphasized the symbolic nature of cognition. However, semantic closure with its description based selected self-organization is not reiterating this position. The symbolic component of open-ended evolutionary systems is stressed, but the material, dynamic, self-organizing characteristics of matter are equally stressed. It is the ultimate inclusive approach which is neither reductionist nor dualist [Pattee, 1995]. While it is maintained that a purely physical description or dynamics will not explain symbolic function (as several material systems may implement the same function), it is also maintained that different material structures will not have identical domains of potentially evolvable functions. The important idea is that evolution relies both on self-organization and selection, and only those self- organizing systems able to harness their dynamics to obtain a symbolic dimension can have open-ended evolutionary potential.

4 Evolving semiotics: a conceptual framework for inclusive self-organization

Semiotics concerns the study of signs/symbols in three basic dimensions: syntactics (rule-basedoperations between signs within the sign system), semantics (relationship between signs and the world external to the sign system), and pragmatics (evaluation of the sign system regarding the goals of their users) [Morris, 1946]. The importance of this triadic relationship in any sign system has been repeatedly stressed by many in the context of biology and genetics [e.g. Waddington, 1972; Pattee, 1982, 1995]; in particular, Peter Cariani [1995] has presented an excellent discussion of the subject. We can understand the semiotics of the genetic system if we consider all processes taking place before translation (from transcription to RNA editing) as the set of syntactic operations; the relation between mRNA (signifier) and folded amino acid chains (signified), through the genetic code, as the implementation of a semantic relation; and finally, the selective pressures on the obtained proteins as the pragmatic evaluation of the genetic sign system.

4.1 Semiotics with two symbol types

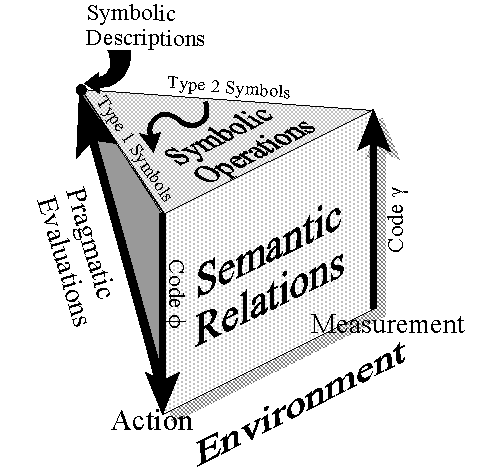
Until now, the semiotics of DNA has been considered strictly unidirectional: DNA stands for proteins to be constructed. In other words, the symbolic DNA encodes (through the genetic code) actions to be performed on some environment. Naturally, through variation and natural selection (pragmatic evaluations) new semantic relations are created which are better adapted to a particular environment, however, real-time contextual measurements are not allowed by this unidirectional semiotics. If in addition to symbols standing for actions to be performed, the genetic system is also allowed a second type of symbols standing for contextual, environmental, measurements, then a richer semiotics can be created which may have selective advantage in rapidly changing environments, or in complicated, context dependent, developmental processes. Figure 2 depicts such a sign system. The top plane contains two different types of symbols which are combined in different ways (symbolic operations). Type 1 symbols stand for actions through a code φ (e.g. the genetic code) and type 2 symbols stand for measurements through a different code γ which is being hypothesized here. In Rocha [1995c] evidence was presented to show that RNA editing may be seen as a mechanism for this contextual input, at least for certain well known living organisms like the african trypanosomes [Benne, 1993], and as a potentially important mechanism in the morphogenesis of highly evolved animals [Lomeli et al, 1994]. 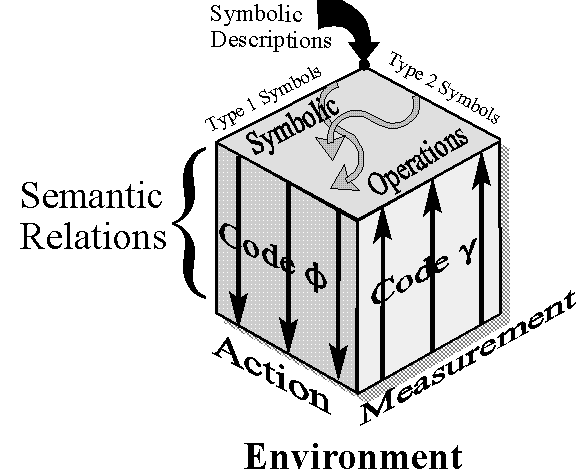We can think of DNA as a set of symbolic descriptions based on two types of symbols: type 1 symbols are expressed in mRNA molecules and stand for actions to be performed; type 2 symbols are expressed in some sort editing mechanisms (e.g. gRNA molecules in the genetic system of the african trypanosomes) which stand for contextual observables. RNA editing can be seen as a set of symbolic operations performed with symbols of both types, resulting in symbols of type 1 to be translated into actions by the genetic code.

Notice that code γ is proposed here as an abstraction referring to the set of mechanisms which will link environmental measurements (context) into type 2 symbols. It is not expected to function as a proper genetic code. Jon Umerez [1995] has stressed the importance of a code in any form of evolving semiotics. In simple terms, what I refer to as a code here is any mechanism able to relate "inert" material structures to other material structures with some functional dynamics "by virtue" of a larger organizational closure. In other words, thefunction of the first material structures is not dependent on its particular materiality, but on what they are used to refer to for the imbedding, material, self-referent semantic closure [Pattee, 1995]. 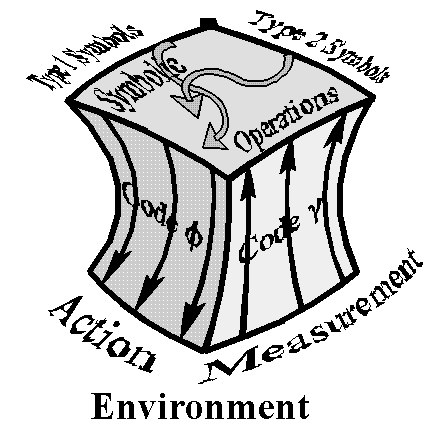Again, a semantically closed system, endowed with this kind of symbol/matter code is able establish open-ended evolution [Pattee, 1995; Umerez, 1995]. Leaving pragmatic evaluations (selection) out of the picture momentarily, the semantic closure with two symbol types, which is able to act as well as perform measurements on its environment can be represented by the cube in figure 3. The semiotic triadic relationship is only complete when individual semantic closures are coupled to an environment (measured and acted upon by each one of them) which ultimately selects (pragmatic evaluation) the most fit amongst these symbol-matter closures (e.g. in natural selection, those that reproduce the most).

4.2 Materiality and implementation dependence: self-organization and selection come together

The issue of materiality is extremely important for two reasons: (i) all which can be represented in this evolutionary semiotics is restricted to what can be constructed by the specific, material, semantically closed system in the first place; and (ii) selection is ultimately performed on this specific material organization capable of performing a number of functions in an environment. The conceptual framework put forward by this material, evolutionary, semiotics forces self-organization and selection together as two indispensable dimensions of evolutionary systems. Pragmatic evaluations or selection takes place on particular dynamics, on the other hand, open-ended evolution is only possible through the existence of a symbolic dimension mediated through a code. Moreover, this code must be built out of some materiality which constrains its representation power and which also ultimately defines eigenbehavior, or an organism's ability to construct and discriminate its environment. This last point raises the issue of implementation-independence and multiple realizability [Umerez, 1995].

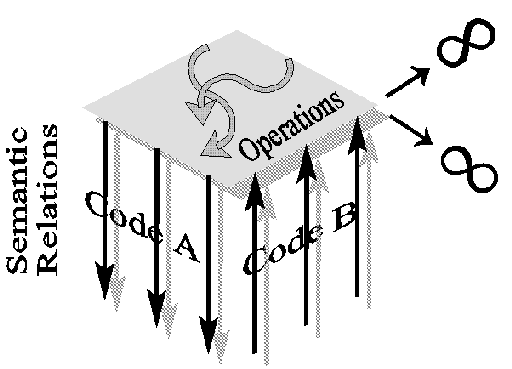A semantically closed system is not implementation independent because matter constrains its eigenbehavior as well as its evolutionary potential. The second constraint is clear when we realize that two distinct closures which at some point establish the same eigenbehavior (the same representational function), if materially different, will evolve differently. The first constraint is not so clear since we hypothetically allow the idea that two different closures can have the same representational function. However, this equivalence can only be established between formal symbol systems which by definition are not materially constrained and are therefore universal, that is, the set of possible semantic relations is infinite (figure 4). Material symbol systems do not have this property. A coding relation must be formed out of certain available material parts in each domain (e.g. nucleotides and aminoacids in the genetic code), and no semantic relation can escape them. In the genetic system we can represent any protein, but we cannot represent and construct any other material structure which is not made out of aminoacid chains. Thus, our semiotics are necessarily constrained by matter, not just due to selection pressures, but on account of the parts available for the symbol system itself (figure 5).

Material sign systems are not universal and cannot represent anything whatsoever, but this turns out to be their greatest advantage. The price to pay for the universality of formal symbol systems is complete specificity, that is, full description of its components and behavior. Conversely, material sign systems are built over certain building blocks which do not need a description. For instance, DNA does not need toencode anything but aminoacid chains, there is no need to include in genetic descriptions information regarding the chemical constituents of aminoacids nor instructions on how to fold an aminoacid chain -- folding comes naturally from the dynamical self-organization of aminoacid chains. Notice how a logical simulation of these genetic mechanisms needs to include all this information that comes free when the self-organizing characteristics of matter are actually used rather than simulated [Moreno et al, 1994].

5 What does it mean for applications?

5.1 Evolutionary strategies: selection alone

The underlying idea of computational evolutionary strategies (ES) is the separation of solutions for a particular problem (e.g. a machine) from descriptions of those solutions through a code. Genetic algorithms (GA's) work on these descriptions and not on the solutions themselves, that is, variation is applied to descriptions, while the respective solutions are evaluated, and the whole (description-solution) selected according to this evaluation. This separation follows von Neumann's self-reproducing scheme which is able to increase the complexity of the machines described. This leads to the conclusion that the form of organization attained by GA's is not self-organizing in the sense of a boolean network or cellular automata. Even though the solutions are obtained from the interaction of a population of elements, and in this sense following the general rules usually observed by computationally emergent systems, they do not strictly self-organize since they rely on the selective pressures of some fitness function. The order so attained is not solely a result of the internal dynamics of a collection of interacting elements, but also dictated by the external selection criteria. To say that the populations of descriptions of solutions self- organize at all in ES may stretch the concept of self-organization a bit too far. ES rely on different concepts: first, with the description-solution dichotomy the concept of local memory is introduced; second, the transition rules of ES are not state-determined _ variation is stochastic; third, as already discussed, selection is external to the populations of descriptions. This way, we can hardly say that a population of memories is interacting with any sort of "self-dynamics": the solutions reached by a GA do not self-organize but are a result of external variation and selection. For all these reasons, it is therefore natural to think of ES as completely distinct from self-organization. It is perhaps useful to think of ES as modeling a very different aspect of biological systems that has to do with natural selection. Self- organizing systems model the abstract, internal, characteristics of matter, while ES model the existence of, external, selective pressures on populations of varying memory based descriptions of some system.

5.2 Artificial semantic relations: the origin problem

The coded relationship between descriptions and solutions for some task in ES is imposed at the onset by the users of such systems. Likewise, the database symbols of some artificial intelligence program are externally related to some categories its users are interested in. Both have to do with the issue of representation in computational domains. All formal systems must have their symbols related to some meaning by the external intervention of some user [Rocha, 1995b], in other words, a formal system cannot change the signifier/signified primitives imposed when it is started, and create new observables [Cariani, 1991]. In the field of GA's some [Mitchell and Forrest, 1994] have been calling for more research to be done on schemes that may allow the evolution of the description/solution relationship itself, that is, the evolution of a code. The same quest takes place in cognitive science for some way to ground the symbols of artificial intelligence models [Harnad, 1990].

Basically, everyone is one way or another dealing with the origin of symbols problem, or in other words, the matter/symbol problem. Some explain symbols away by searching explanations in the dynamics of cognitive and biological systems [e.g. Churchland and Sejnowski, 1991] while others, usually in strong computationalist fields, will look solely at the purely symbolic aspects of complicated systems. Few havebeen calling for the inclusion of both aspects into complementary approaches [Pattee, 1978; Lakoff, 1987; Cariani, 1987; Varela, Thompson, and Rosch, 1991; Etxeberria, 1995]. This latter view calls for an embodiment of models of life and cognitionin such a way as to be able to study the origin problems within an inclusive framework where material and computational aspects are intertwined.

In any case, however far we may be from solving any problems of origin, we may still recognize that both life and cognition rely on complementary dynamical and symbolic characteristics. Even if we do not yet know how these aspects ever came to be brought together, we should build artificial models using both of these aspects (or their simulations) to our advantage, since they have proved to be immensely powerful for natural organisms. For instance, in [Rocha, 1995c], even though using a fixed computational coding relations between descriptions and solutions in a GA, I proposed the establishment of, stochastic, contextual constraints on this coding relation following the basic mechanisms of RNA editing found in a variety of living organisms. These contextual GA's, though completely computational, are able to change the way they produce solutions from the same genetic description, according to changes in their environments. They are an instance of the two symbol type semiotic model discussed in section 3, and can be said to evolve an internal control of genetic expression which may be of use for organisms whose environment is subjected to cyclic changes.

5.3 Genetic algorithms and development: self-organization and selection in Artificial Life

Lately much attention has been posited on evolutionary strategies that bring together self-organizing systems and natural selection inspired algorithms. Particularly in the field of Artificial Life, Kitano[1994], and Dellart and Beer [1994], have proposed GA's which do not encode directly their solutions, but rather encode generic rules (through L-Systems) which develop into boolean networks simulating given metabolic cycles. With these approaches, GA's no longer model exclusively selection, but also a self- organizing dimension standing for some materiality. The GA does not search the very large space possible solutions, but a space of basic rules which can be manipulated to build different self-organizing networks. These networks are then started (sometimes with some learning algorithm) and will converge to some attractor behavior standing for a solution of our simulation. Rather than directly encoding solutions, the GA harnesses a space of possible self-organizing networks which will themselves converge to a solution -- emergent morphology.

The computational advantage of these systems lies on the tremendous reduction of the algorithm's search space since the solutions do not have to be encoded in all details, the emergent morphology "takes care" of details we do not need to encode. In particular, I have proposed a developmental scheme [Rocha, 1995c] which uses the same search space (based on fuzzy rules) for whatever number of simulation primitives we desire, in other words, a generic GA which uses the same state space regardless of the simulation task by utilizing an emergent morphology scheme based on fuzzy logic. By simulating both selection and self-organization, the size of descriptions is dramatically reduced, and an avenue is opened for studying the simulation of both the symbolic and material aspects of evolutionary systems.

5.4 Categorization and constructivism: uncertainty and belief in artificial intelligence

Eleanor Rosch [1978] and George Lakoff [1987], among others, have stressed the importance of an embodiment of cognition to deal with its representation issues. In Rocha [1994b, 1995d, 1995e] I have introduced a set structure called evidence set based on fuzzy logic and the Dempster-Shafer [Shafer, 1976] theory of evidence. These structures allow the inclusion of all forms of uncertainty recognized in information theory [Klir, 1993] as well as a formalization of belief and contextual dependencies in a set format. Evidence sets do not specifically include an account of materiality, however, the formalization of belief and context allows larger imbedding models of cognitive categorization to base the belief andcontextual strengths of concept membership on specific material constraints, or its simulation through, say, neural networks.

The contextual pointers of evidence sets are related to Pask's [1976] P-individuals in his conversation theory and are thus embedded in a constructivist framework which emphasizes the construction of a reality in terms of a cognitive system's specific materiality and environmental coupling. This is also a direct result of von Foerster's formulation of eigenbehavior and an aid to establishing another instance of the semiotic model of section 3 in the cognitive realm. It can be seen to offer a constructivist position of representation which stresses embodiment, but must also, on the other hand, concede that in an evolutionary context, the construction of categories must have a representational relation to aspects of the organism's environment, or its categorization would not have survival value in that particular organism/environment structural coupling [Medina-Martins and Rocha, 1992; Rocha, 1995d]. In other words, embodiment does not eradicate the necessity to still explain some sort of representational relation between constructed categories and the cognitive system's context.

6 Conclusions: selection meets self-organization

I have stressed that though self-organizing systems with distributed memory represent a minimum requirement for evolutionary systems, their evolutionary potential is much larger, possibly open-ended, if further endowed with dynamically "inert" structures to be used by their classification mechanisms. It was stressed that this by no means entails a return to purely symbolic approaches to cognition, nor a belief in the absolute sovereignty of natural selection in evolution. Rather, it is a call for more inclusive, hybrid approaches to such evolutionary and learning systems. In artificial Life this implies building models which bring together self-organizing mechanisms, such as cellular automata or boolean networks, with genetic algorithms (with varying degrees of control of their genetic expression). In Artificial Intelligence it implies the establishment of models able to go beyond connectionist classification, by inclusion of higher level accounts of cognitive categorization.

7 References

Benne, Rob (Ed.) [1993]. RNA Editing: The Alteration of Protein Coding Sequences of RNA. Ellis Horwood.

Cariani, Peter [1991]."Some Epistemological Implications of Devices which Construct their own Sensors and Effectors." In: Towards a Practice of Autonomous Systems. Varela and Bourgine (Eds.). MIT pp 484-493.

Cariani, Peter [1995]."Towards an evolutionary semiotics: the role of symbols in organisms and adaptive devices." In: Proc. of the ISES Vienna 1995. Stanley Salthe and Gertrudis Van de Vijver (eds). In Press.

Churchland, Patricia S. and T.J. Sejnowski [1992]. The Computational Brain. MIT Press.

Conrad, Michael [1983]. Adaptability. Plenum Press.

Conrad, Michael [1990]."The geometry of evolutions." In: BioSystems Vol. 24, pp. 61-81.

Dellaert, F. and R.D. Beer [1994]."Toward an evolvable model of development for autonomous agent synthesis." In: Artificial Life IV. R. Brooks and P. Maes (Eds.). MIT Press.

Etxeberria, Arantza [1995]."Embodiment of Natural and Artificial Systems." In: Proceedings of the International Seminar on Evolutionary Systems, Vienna 1995. G. van de Vijver and S. Salthe (Eds.). In Press.

Haken, H. [1977]. Synergetics. Springer-Verlag.

Harnad, Stevan [1990]."The symbol grounding problem." In: Emergent Computation. S. Forrest (Ed.). MIT Press.

Kampis, George [1991]. Self-Modifying Systems in Biology and Cognitive Science. .

Kauffman, S. [1993]. The Origins of Order: Self-Organization and Selection in Evolution. Oxford University Press.

Kitano, Hiroaki [1994]."Evolution of Metabolism for Morphogenesis." In: Artificial Life IV. Brooks, R.A. and P. Maes. MIT Press. pp 49-58..

Klir, George J. [1991]. Facets of Systems Science. Plenum Press.

Klir, George J. [1993]."Developments in uncertainty-based information." In: Advances in Computers. M. Yovits(Ed.). Vol. 36, pp 255-332.

Lakoff, G. [1987] Women, Fire, and Dangerous Things. Chicago University Press.

Maturana, H., and F. Varela [1987]. The Tree of Knowledge. New Science Library.

Medina-Martins, Pedro R. and Luis Rocha [1992]."The in and the out: an evolutionary approach." In: Cybernetics and Systems Research '92. Robert Trappl. World Scientific Press. pp 681-689.

Mitchell, M. and S. Forrest [1994]."Genetic algorithms and Artificial Life." In: Artificial Life Vol. 1, pp 267-289.

Moreno, A., A. Etxeberria, and J. Umerez [1994]."Universality without matter?." In: Artificial Life IV. R. Brooks and P. Maes (Eds). MIT Press, pp.406-410.

Morris, Charles W. [1946]. Signs, Language, and Behavior. G. Braziller, New York.

Nicolis, G. and I. Prigogine [1977]. Self-Organization in Nonequilibrium Systems

Packard, N. [1988] "Adaptation to the edge of chaos". In: Complexity in Biologic Modelling. Kelso and Shlesinger

Pask, Gordon [1976]. Conversation Theory: Applications in Education and Epistemology. Elsevier.

Pask, Gordon [1992]."Different kinds of Cybernetics." In: New Perspectives on Cybernetics. Gertrudis Van de Vijver (Ed.). Kluwer Academic Publishers. pp. 11-31.

Pattee, Howard H. [1978]."The complementarity principle in biological and social structures." In: Journal of Social and Biological Structures Vol. 1, pp. 191-200.

Pattee, Howard H. [1982]."Cell psychology: an evolutionary approach to the symbol-matter problem." In: Cognition and Brain Theory Vol. 5, no. 4, pp 325-341.

Pattee, Howard H. [1995]."Evolving self-seference: matter, symbols, and semantic closure." Communication and Cognition - AI Vol. 12, nos 1-2 (Rocha [1995a]). pp. 9-27 .

Prigogine, I. [1985]."New perspectives on complexity." In: The Science and Praxis of Complexity. United Nations Library. Reprinted in Klir [1991], pp. 483-492.

Rocha, Luis M. [1994a]."Von Foerster's cognitive tiles: semantically closed building blocks for AI and Alife." In: Cybernetics and Systems ' 94. Robert Trappl (Ed.). Vol. 1, pp 621-628. World Scientific Press.

Rocha, Luis M. [1994b]."Cognitive Categorization revisited: extending interval valued fuzzy sets as simulation tools for concept combination." In: Proc. of the 1994 Int. Conf. of NAFIPS/IFIS/NASA. IEEE. pp 400-404.

Rocha, Luis M. (Ed.) [1995a]. special issue in Self-Reference in Biological and Cognitive Systems. Communication and Cognition - Artificial Intelligence Vol. 12, nos. 1-2

Rocha, Luis M. [1995b]."Artificial semantically closed objects." Communication and Cognition - AI Vol. 12, nos. 1- 2 (Rocha[1995a]). pp. 63-90.

Rocha, Luis M. [1995c]."Contextual Genetic Algorithms: Evolving Developmental Rules." In: Advances in Artificial Life. F. Moran, A. Moreno, J.J. Merelo, and P. Chacon (Eds.). Springer-Verlag. pp. 368-382.

Rocha, Luis M. [1995d]."(Interval based) Evidence Sets: Modelling Subjective Categories." In: International Journal of General Systems In Press.

Rocha, Luis M. [1995e]."Computing Uncertainty in Interval Based Sets." In: Applications of Interval Computation. R.B. Kearfott and V. Kreinovich (Eds.). Kluwer. (In Press).

Rosch, E. [1978]."Principles of Categorization." Cognition and Categorization. Rosch and Lloyd (Eds.).Hillsdale.

For more information contact Luis Rocha at rocha@indiana.edu.
Last Modified: September 02, 2004