Evidence Sets and Contextual Genetic Algorithms

This dissertation proposes a systems-theoretic framework to model biological and cognitive systems which requires both self-organizing and symbolic dimensions. The framework is based on an inclusive interpretation of semiotics as a conceptual theory used for the simulation of complex systems capable of representing, as well as evolving in their environments, with implications for Artificial Intelligence and Artificial Life. This evolving semiotics is referred to as Selected Self-Organization when applied to biological systems, and Evolutionary Constructivism when applied to cognitive systems. Several formal avenues are pursued to define tools necessary to build models under this framework.

In the Artificial Intelligence camp, Zadeh's Fuzzy Sets are extended with the Dempster-Shafer Theory of Evidence into a new mathematical structure called Evidence Sets, which can capture more efficiently all recognized forms of uncertainty in a formalism that explicitly models the subjective context dependencies of linguistic categories. A belief-based theory of Approximate Reasoning is proposed for these structures, as well as new insights as to the measurement of uncertainty in nondiscrete domains. Evidence sets are then used in the development of a relational database architecture useful for the data mining of information stored in several networked databases. This useful data mining application is an example of the semiotic framework put into practice and establishes an Artificial Intelligence model of Cognitive Categorization with a hybrid architecture that possesses both connectionist and symbolic attributes.

In the Artificial Life camp, Holland's Genetic Algorithms are extended to a new formalism called Contextual Genetic Algorithms which introduces nonlinear relationships between genetic descriptions and solutions for a particular problem. The nonlinear relationship is defined by an indirect scheme based on Fuzzy Sets which implements the simulation of dynamic development after genetic transcription. Genetic descriptions encode dynamic building blocks that self-organize into solutions. Since the self-organizing process may depend on environmental information, the process is thus contextualized. The main advantage of this scheme is the ability to reduce dramatically the information requirements of genetic descriptions, it also allows the transformation of real-encoded to binary-encoded problems. The scheme is used successfully to evolve Neural Network architectures as well as Cellular Automata rules for non-trivial tasks. It is also used to model the biological process of RNA Editing. Contextual Genetic Algorithms are an instance of the semiotic framework proposed and of Selected Self-Organization in particular.

Keywords: Complex Systems, Systems Science, Adaptive Computation, Evolutionary Algorithms, Artificial Intelligence, Artificial Life, Data Mining, Information Technology, Fuzzy Logic, Interval-Valued Fuzzy Sets, Dempster-Shafer Theory of Evidence, Uncertainty, Cognitive Categorization, Context, Relational Databases, Embodiment, Constructivism, Self-Organization, Natural Selection, Evolutionary Systems, Semiotics, Representation, RNA Editing, Development, and Situated Cognition.

Dedication

To my family

who cultivated in me the notion of knowledge as power,

and

who gave me all the support and love needed to try to achieve it.

Acknowledgments

Many people, ideas, and places have influenced and contributed, directly and indirectly, to this dissertation. More or less chronologically, I would especially like to thank:

My parents for unreserved love, support, and encouragement. À Mãe por todos os sacrifícios que nos tem dedicado, e também por me mostrar que podemos sempre fazer melhor. Ao Pai pela inspiração em todas as coisas científicas que despoletou em mim, e por sempre me apoiar mesmo nas decisões mais ousadas.

My brother for being my life long best friend, and trusting me beyond any doubt. Todos aqueles telefonemas deliciosos pela manhã, acredita, foram inúmeras vezes aquela "forcinha" necessária para passar os problemas do dia a dia de cabeça erguida.

The few teachers from junior to high school who took the extra time to deal with me! In particular my Physics, Philosophy and Geometry teachers.

Barata Marques and Luciano Faria for giving me a hand in college.

Helen Swannell for showing me sweetness in life. Thanks for your dreams and passions!

Pedro e Guida Medina Martins for encouraging my ambitions.

Francisco Carvalhal for such strong guidance and teaching me the pleasure of team work.

Susana Santos for truly happy times e muita paciência!

Gordon Pask, Heinz von Foerster, and Gerard de Zeeuw for encouraging me beyond words, and pointing the way towards a more humanistic science. Thank you so much!

Francis Heylighen and Cliff Joslyn for really getting me into this Systems Science thing.

Chuck Henry and Nancy Todd for opening the door and for listening power.

George Klir for unbounded interest and guidance. Thank you for such creativity, hard work, and willingness to foster my pursuits.

Howard Pattee first for swamping me with such an array of interesting problems, and then for proposing the most eloquent and balanced solutions. Thank you for discussing and reading my often half-baked manuscripts with such prompt response.

Don Gause for making me work 16 hours a day happily! Thank you for all the time and interest in discussing myriad different problems, and for truly inspirational teaching methods.

Eileen Way for captivating discussions over the connectionist debate, and for making me put reason where there was only blabber.

John Dockery for amazing support and interest. I owe the condensation of this dissertation into a presentable shape to an evening of your guidance.

Fernando Carvalho Rodrigues for tremendous support and creativity!

Howard Pattee's and George Klir's research groups for most intersting discussions and comments: especially Robin Beckerman, Bo Yuan, David Harmanec, Ute St. Clair, George Fridrich, Ira Glickestein, Barbara Harris, and Dario Nardi.

All those who have contributed to the ideas here pursued with lively debates, presentations, or overall scientific support: Gertrudis van de Vijver, Jon Umerez, Peter Cariani, Eric Minch, Robert Rosen, George Kampis, Arantza Etxeberria, Bernard de Baets, Vladik Kreinovich, Stan Salthe, Jerry Chandler, Gert de Cooman, Alvaro Moreno, Ranulph Glanville, Clara Pinto Correia, Erich Prem, Melanie Mitchell, Wim Hordik, John Casti, and many others .

My life long friends so necessary to maintain my sanity. Tomi Erkkila for being my buddy and having the patience to, among other things, ski with me -- Tracey, you are a lucky girl! Manuel Cardenas for unbelievable patience, friendship, and mathematical help (and chicken wings!). Virginia Cole for being such a source of stability in graduate school (and all the movies!). Jon Umerez and Gabriela Chotro for being so sane! Jon, thanks for all sorts of most valuable discussions. Matt Hochberg (for musical satisfaction), Maureen O'Connor (for those wonderful action-packed days!), Dolly Varkey (oh the Rat!), Marco Busatto (for not really wussing out), Sezai Dogdu (Thursday night fever!), Johan Bollen (the coolest net dude!), Jim Gattiker, Ray Barnes, Olokunmi Johnson, Carolin Auer, Tabea Linhard (the world needs a Tambourine Girl!), Mina Caravagio, Amy McNichols, Michella Scotto, Thomas Uthup, and all other friends who I do not name here.

Debbie, thank you for your love and patience so dearly appreciated especially in this final "dissertating" stretch.

The work here presented was supported from 1992 to 1996 by a scholarship awarded by the Programa CIENCIA, Junta Nacional de Investigação Científica e Tecnológica, Lisbon , Portugal.

TABLE OF CONTENTS

CHAPTER 1

INTRODUCTION 1

Motivation 1

Preliminary Background 2

Aims and Claims 5

Outline 5

Application Areas 8

CHAPTER 2

SELECTED SELF-ORGANIZATION AND EVOLUTIONARY CONSTRUCTIVISM 9

1. Selected Self-Organization 9

1.1 Self-Organization 9

1.2 Emergent Classification and Constructivism 10

1.2.1 Cybernetics and Eigenbehavior 10

1.2.2 Complexity Theory, Emergent Representation, and Emergent Morphology 10

1.2.3 Self-Organization and Constructivism 12

1.3 Emergence and Levels of Description 12

1.3.1 Explanatory Emergence 13

1.3.2 Semantic Emergence 14

1.4 Memory and Selected Self-Organization 15

1.4.1 Variety of Classification and the Edge of Chaos 15

1.4.2. Structural Change and Emergent Classification 16

1.4.3 Distributed Memory 17

1.4.4 Embodiment 18

1.5 Descriptions and Symbols 18

1.5.1 Von Neumann and Description-Based Selection 18

1.5.2 Descriptions require a Symbol System 19

1.5.3 Parts, Symbols, and Embodiment 20

1.5.4 The Symbolic Advantage 20

1.6 Semantic Closure and Open-Endedness 21

1.6.1 Finite Symbol-Part System 22

1.6.2 Dynamic Part Compounds 22

1.6.3 Development: Constraints on Evolution 23

1.6.4 Selected Self-Organization with Local Memory 24

1.6.5 The Credit Assignment Problem 24

1.7 Evolving Semiotics 25

2 Evolutionary Constructivism 26

2.1 Material Basis: Selected Self-Organization and Constructivism 27

2.1.1 Radical Constructivism 27

2.1.2 Physical Constructivism 28

2.1.3 Constructionism 29

2.1.4 Situated Cognition 29

2.2 Realism and Evolutionary Epistemology 30

2.3 Critical Realism 31

2.4 Language Theory and Evolutionary Constructivism 32

2.4.1 Selected Self-Organization 33

2.4.2 Improving Structural Perturbation 34

2.4.3 Metaphor 35

2.4.4 Constraints and Evolutionary Contructivism 35

CHAPTER 3

EVIDENCE SETS: CONTEXTUAL CATEGORIES 37

1. Cognitive Categorization 37

1.1 Models of Cognitive Categorization 38

1.2 The Classical View 38

1.3 Prototype Theory and Fuzzy Sets 39

1.4 Dynamic Categories 40

1.5 Fuzzy Objectivism 41

2. Mathematical Background 41

2.1 Measures 41

2.2. Dempster-Shafer Theory of Evidence 42

2.2.1 Basic Probability Assignment 42

2.2.2 Belief and Plausibility 42

2.2.3 Focal Elements and Bodies of Evidence 43

2.2.4 Dempster's rule of combination 43

2.2.5 Joint Bodies of Evidence 43

2.2.6 Inclusion 44

2.3 Fuzzy Sets and Interval Valued Fuzzy Sets 44

2.4 Uncertainty 45

2.4.1 Conflict 46

2.4.2 Nonspecificity 47

2.4.3 Fuzziness 47

3. Sets and Cognitive Categorization 48

3.1 Fuzzy Sets and the Prototype Combination Problem 48

3.2 Interval Valued Fuzzy Sets 49

3.3. Set complement and intuitionistic sets 50

4 Evidence Sets: Membership and Belief 51

4.1 Consonant Evidence Sets 51

4.2 Non-Consonant Evidence Sets 52

4.3 Complexity of Computation 52

4.4 Contextual Interpretation of Evidence Sets 52

5. Relative Uncertainty and Evidence Sets 54

5.1 Nonspecificity 54

5.1.1 A General Measure 54

5.1.2 Absolute Nonspecificity 55

5.1.2 Relative Nonspecificity 59

5.2 Conflict 62

5.2.1 Absolute Conflict 62

5.2.2 Relative Conflict 63

5.3 Fuzziness 64

5.4 3-D Uncertainty 65

5.4.1 Nonspecificity in Evidence Sets 65

5.4.2 Conflict in Evidence Sets 66

5.4.3 3-D Uncertainty Cube 66

6. Belief-Constrained Approximate Reasoning 67

6.1. Uncertainty Increasing Operations Between Evidence Sets 67

6.1.1 Complementation 67

6.1.2 Intersection 68

6.1.3 Union 68

6.1.4 Increasing Uncertainty 68

6.2 Uncertainty Decreasing Operation Between Evidence Sets 68

6.3 The Pet-Fish Example 70
72

7.1 Upper and Lower Probabilities Interpretation 72

7.2 Belief Interpretation 72

7.3 Generalized Dempster-Shafer Theory 73

7.4 Evidence Sets : Independent Membership 73

CHAPTER 4

CONTEXTUAL GENETIC ALGORITHMS 75

1 Models with both Dynamic and Selective Dimensions 75

2 Semiotics of Living Organizations 75

2.1 Two Type Symbol System: Contextual Environmental Information 76

2.2 Embodiment and Implementation Dependence: Selected Self-Organization 77

3. Contextual Genetic Algorithms 78

4. Exploring Syntax and RNA Editing 80

4.1 RNA Editing 80

4.2 A Formal Model of Genetic Editing 83

5. Development and Material Constraints 87

5.1 Development in Artificial Life 87

5.2 Fuzzy Development Programs: Emergent Classification in Contextual Genetic Algorithms
88

5.2.1 Fuzzy Sets as Dynamical States 88

5.2.2 Fuzzy Development Programs 90

5.2.3 Information Requirements of Fuzzy Development Programs 90

5.2.4 General Purpose Genetic Algorithm with Developmental Indirect Encoding: Emergent Classification 92

5.2.5 Computational Issues: Fuzzy Indirect Encoding as Solution Approximation 93

CHAPTER 5

IMPLEMENTING CONTEXTUAL STRUCTURES FOR DATA MINING 95

1. Computing Categories in Relational Databases: Linguistic Categories as Consensual Selection of Dynamics 95

1.1 Nakamura and Iwai's Fuzzy Information Retrieval System 96

1.1.1 The Long-Term Networked Memory Structure: Semantic Closure 97

1.1.2 Short Term Categorization Processes 97

1.1.3 Document Retrieval 99

1.1.4 Adaptive Alteration of Long-Term Structure by Short-Term Categorization: Pragmatic Selection 100

1.2 Contextual Expansion With Evidence Sets 101

1.2.1 Distances from Several Relational Databases: The Extended Long-Term Memory Structure 101

1.2.2 Extended Short-Term Categorization 102

1.2.3 Document Retrieval 105

1.2.4 Adaptive Alteration of Long-Term Structure 105

1.2.5 Categories as Linguistic, Metaphorical, Structural Perturbation 105

1.2.6 Open-Ended Structural Perturbation 106

1.2.7 TalkMine: The Implemented Application 106

2. Emergent Morphology and Evolving Solutions in Large State Spaces 112

2.1 Implementation Details 112

2.2 Continuous Variables: Evolution of Neural Network Weights 113

2.2.1 Hand-Written Character Recognition: The Network Architecture 113

2.2.2 Results from Back-Propagation 114

2.2.3 Results from Real-encoded GA 115

2.2.4 Results from CGA with Fuzzy Indirect Encoding 117

2.3 Discrete Variables: Evolution of Cellular Automata Rules 119

2.4 The Effectiveness of Computational Embodiment: Epistasis and Development 124

CHAPTER 6

SIMULATIONS OF EMBODIED EVOLVING SEMIOSIS 126

1. What Would Invalidate EES? 128

2. What Does EES Have to Offer to AI and AL? 129

2.1 Evolutionary Constructivism and AI 129

2.2 Selected Self-Organization and AL 131

3. Limitations of EES 131

3.1 The Origin Problem 131

3.2 Computational Limitations 132

4. Future Directions and Conclusions 133

REFERENCES 135

INDEX 144

CHAPTER 1

INTRODUCTION

"In recent years increasing need has been felt for a body of systematic theoretical constructs which will discuss the general relationships of the empirical world. This is the quest of General Systems Theory... Somewhere however between the specific that has no meaning and the general that has no content there must be, for each purpose and at each level of abstraction, an optimum degree of generality." [Boulding, 1956, page 197]

"The essence of mental life and bodily life are one, namely "the adjustment of inner to outer relations." [James, 1892, page .xxviii]

"The question of how symbols acquire semantics has been subsumed [in Artificial Intelligence and Artificial Life] into questions of syntax, how symbols relate to each other. And just as systematically, questions of pragmatics, why symbols come to have the semantic and syntactic relations they do, have been left out of the picture entirely." [Cariani, 1989, page vii]

Motivation

To define general relationships in the empirical world is the quest of Systems Science. The price of generalization, however, may be the curse of the cybernetic age, as widely encompassing synthetic theories, armed with powerful computer resources, tend to disregard the intricacies of particular systems. I am particularly impressed by attributes shared by cognitive and biological systems. Are these attributes only relevant if we abstract such systems enough, or are they at the core of the distinctions that uniquely classify living and cognitive systems? Furthermore, can we and do we have anything to gain from incorporating such attributes in computational applications?

The commonality I see follows from the symbolic/representational attributes of life and cognition. Unfortunately, symbol and representation are terms that carry a heavy weight of undesirable connotations. It is often argued that symbols are subjective constructs unnecessary to explain living and cognitive systems, which are nothing but highly interconnected networks of bio-chemical processes following perfectly determined rules. According to this view, these rules are all we need to explain biology and cognition. Some further argue that accepting a symbolic and representational dimension is misleading because living and cognitive systems do not represent an environment but rather construct it with the stabilities produced by the dynamics of their constituent bio-chemical networks. This view is often referred to as the self-organizing paradigm.

On the other extreme of the materialist and constructivist view above, are those identified with the symbolic paradigm who think of symbols as purely computational constructs. This form of computationalism defines representation as the mapping of categories from one domain to another: from environmental to genetic or mental categories. It thus ignores the material constraints of biological and cognitive systems, which are considered irrelevant to define such systems, accepting genetic and mental categories as mirroring (through the mapping) real world categories. The term representationalism has been identified with this view.

I shall argue that both representational and self-organizing approaches avoid the central issue of how matter and symbols co-evolve. Representationalism denies the particular aspects of a system's embodiment, while the self-organizing paradigm refuses to accept the evolutionary advantage of a pragmatic (selected), symbolic, relationship with an environment. I believe that an inclusive approach should be pursued which considers the syntactic, semantic, and pragmatic aspects of living and cognitive systems. Pragmatism is understood as a context-dependent, multi-level constraint satisfaction of material, developmental, and evolutionary requirements. Furthermore, this semiotic approach though general enough to encompass biology and cognition, should offer a set of specific requirements to distinguish living and cognitive systems from other complex systems, defining a valid systems theoretic conceptual framework. My motivation is precisely geared to add some more concepts and tools for the establishment of such a framework already proposed by other systems researchers with similar goals.

The aim of the present work is to advance arguments to substantiate the view that the modeling of cognitive and biological systems should utilize concepts emanating from both the self-organizing and representationalist paradigms. Indeed, both paradigms offer only an incomplete account of the nature of life, biological or cognitive, which is given a more realistic explanation when both paradigms are understood as complementary. Philosophical and conceptual arguments are given to substantiate this inclusive position, and how it relates to a web of existing philosophical viewpoints. The position is strengthened by the definition of mathematical and computational formalisms which show its relevance in the creation of practical computational applications for information technology.

Preliminary Background⁽¹⁾

Traditionally, Artificial Intelligence (AI) and Artificial Life (AL) have been associated with a computational approach to cognition and biological systems. Models involve systems that manipulate symbols which stand for external observables: a representational scheme. This manipulation follows computational rules, and has lead to the idea of mind and life as a program. With this approach, the particular substrate which implements symbols and rules is irrelevant as long as the desired computation is achieved. It is usually referred to as the Symbolic or Computational Paradigm.

The alternative view, brought back to life in the 1980's with the revival of earlier cybernetic ideas, uses physical laws as the basis of its models. It attempts a dynamic explanation of cognition and life by building models inspired by the dynamics of the brain and living matter. The functions that the symbolic paradigm attempts to directly represent and compute, are seen on this alternative approach as emergent properties of the dynamics. It is usually referred to as a Connectionist, Emergent, Dynamic, Subsymbolic, or Self-Organizing Paradigm:

"One of the most interesting aspects of this alternative approach in cognitive science is that symbols, in their conventional sense, play no role. In the connectionist approach, symbolic computations are replaced by numerical operations - for example, the differential equations that govern a dynamical system. These operations are more fine grained than those performed using symbols; in other words, a single, discrete symbolic computation would, in a connectionist model, be performed as a result of a large number of numerical operations that govern a network of simple units. In such a system, the meaningful items are not symbols; they are complex patterns of activity among the numerous units that make up the network." [Varela, Thompson, and Rosch, 1991 page 99]

The early 1990's were prolific in debates on the differences between the Symbolic and Connectionist paradigms [e.g. Ramsey, Stich, and Rumelhart, 1991 (eds); Dinsmore, 1992 (ed)]. Today, in most of AI, these distinctions have boiled down to the opportunistic utilization of techniques from both camps according to particular aspects of designed applications. Applied AI journals and magazines will just as likely publish the latest advances in expert systems driven by logic engines (classical, modal, or fuzzy), as the latest neural network, cellular automata, or genetic algorithm schemes. In fact, hybrid architectures tend to be the most favored items found on these publications. On a more conceptual level, it has been generally accepted that looking at cognition with symbolic or dynamic tools is a question of finding a comfortable level of description for the properties we desire to model. Those working within a symbolic paradigm are most often preoccupied with models of natural language and human reasoning and categorization processes, while those utilizing dynamic tools focus on pattern recognition and dynamic classification models.

In theoretical biology, evolutionary systems theory, or AL, a similar feud is defined between those that understand life as essentially a genetic variation engine subjected to natural selection (neo-Darwinism, functionalism) [e.g. Dawkins, 1987; Maynard-Smith, 1986; Dennett, 1995], and those that stress that life is essentially a property of the self-organization and development of dissipative material structures (structuralism) [e.g. Thom, 1975; Nicolis and Prigogine, 1977; Haken, 1977; Maturana and Varela, 1987; Kauffman, 1991; Goodwin, 1994]. Unlike what happens in cognitive science, in evolutionary systems theory it has been somewhat easier to propose inclusive approaches based on the hierarchical aspects of biological systems [e.g. Gould, 1989; Pattee, 1974; Salthe, 1985, 1993], though none of these proposals has had the widespread success of the genetic reductionism view.

The symbolic paradigm of AI and the genetic reductionist approach of evolutionary systems can be referred to generally as the representationalist view of life and cognition. Basically, it is based on the existence of discrete, static, entities that linearly stand for phenotypic traits in a living system they uniquely define, or for real world categories that a cognitive system must classify. Natural selection is the process that statistically biases these symbolic entities in population distributions of living systems, resulting in increased phenotypic adaptation to a given environment. The symbolic nature of the heritable results of natural selection, has lead to the widespread success of genetic models of artificial living systems which do not depend on a specific materiality [Langton, 1989]. Cognitive science has not been as lucky in defining an overall process responsible for the adaptation of mental to real world categories, or learning. Natural selection is proposed as an engine for phylogenetic learning in theories of evolutionary epistemology [Lorenz, 1981, Campbell, 1987, Wuketits, 1990] and even account for grammatical constraints of language [Pinker, 1993]. Ontogenetic learning is still very much the subject of theoretical strife. Regardless of the true nature of learning, representationalism considers that mental categories essentially mirror real world categories, and that the material aspects of cognitive systems are largely irrelevant.

The Connectionist paradigm of current day cognitive science, and the structuralist approach to evolutionary systems can be referred to generally as the self-organizing view of life and cognition. It is based on the existence of networks of simple components following simple state-transition rules, whose dynamic global behavior is essentially dependent on a small number (compared to the number of components) of dynamic basins of attraction. The process that leads the system from any initial state to one of the basins of attraction is understood as self-organization. These basins of attractions are not localized in identifiable components, but distributed and superposed [van Gelder, 1991] through the whole network. In evolutionary systems, this view emphasizes that life is largely dependent on the spontaneous organization of order which exists with or without natural selection. Further, evolution is believed to be restricted to the dynamic trajectories of these systems, that is, the history of the attractor landscape of a given dynamics as its structure is perturbed. This implies that not all phenotypic traits, regardless of their fitness in an environment, can be obtained, unless they stem from the set of possible dynamical stabilities in a given dynamic trajectory. In cognitive systems, this view likewise stresses that classification of an environment depends on the existence of dynamic stabilities of connectionist systems. Only those aspects of the environment whose interaction with the network lead to internal stabilities can be recognized and classified.

The morphology of living systems and the classification capabilities of connectionist systems are considered to be emergent properties of a complicated dynamics. That is, a multitude of highly interrelated simple components produce a dynamic behavior not completely described by the operative rules of the components. Morphology and classification are said to be emergent properties of self-organizing networks. But are emergent properties nothing but a different way to look at the complicated dynamics responsible for this emergence (reductionism), or do these properties establish a genuinely novel and distinct organization? At first glance, and if we desire to maintain the non-dualist, materialist, tenets of modern science, we seem to have no choice but to accept the reductionist stance expressed on the first interpretation of emergent properties: everything is ultimately explained by a lower-level dynamic set of laws and distinctions between levels exist only in the eye of the beholder who chooses to work on a particular level of description. The question is thus one of explanatory power and of levels of description.

The present work elaborates the view that emergent properties, though embedded on some lower dynamics, present a true novel organization which is not completely derivable from the lower level descriptions. The notion of emergence here defended is based on the explanatory power of different levels of description, and it is akin to Clark's [1996] recent ideas, which are related to Rosen [1985, 1995] and Cariani's [1989] emergence relative to a model framework. Particularly relevant is the concept of emergent classification which is discussed in detail. I shall argue that emergent classification can be improved when classifying systems are capable of establishing a clear form of symbolic interaction (semiosis) with their environments, which is both effectively representational and dynamically constructed. The argument for this situated semiosis is strongly grounded on Von Neumann's [1966] self-reproducing automata scheme, which is an argument for construction under symbolic control, as well as on an extended formulation of his Parts Problem. Stricter definitions of emergence exist (for a deeper discussion see Cariani [1989], Salthe [1991]), but to pursue my argument, the explanatory notion of emergence will suffice.

Both representational and self-organizing approaches to living and cognitive systems avoid the concept of semiosis. Representationalism denies the particular aspects of a system's situated embodiment with its contextual constraints, while the self-organizing paradigm refuses to address the utility of the concept of symbol and its evolutionary relationship with an environment.

I call for an inclusive approach that considers the syntactic, semantic, and pragmatic aspects of biological and cognitive life. To do this, I develop mathematical and computational tools that improve the simulation of certain mental and biological processes beyond pure representational or pure self-organizing models. These models are imbedded in a selection-grounded Constructivist framework. In other words, classification of an environment is highly dependent on the classifier's dynamical structure, it is not fully open-ended or based on mappings of real world categories to internal categories, but a result of internal construction of stabilities. However, there must be an element of effective representation, or the classifier system would not survive and reproduce in a given environment. This constructed, contextual, intentionality is a result of some form of selection by the environment, which I call evolutionary constructivism.

Aims and Claims

More explicitly, the aim of the present work is to advance an inclusive framework for the systems-theoretic study of biological and cognitive systems that utilizes both self-organization and representation. Such undertaking is pursued by:

Arguing the necessity of complementary levels of description for complex systems (emergence).
Arguing for a more complete understanding of symbol and representation based on the three semiotic dimensions of syntax, semantics, and pragmatics.
Showing that the coupling of symbolic controls to material self-organization defines enabling and restraining constraints on the living organization.
Developing models with self-organizing and symbolic characteristics for AI and AL and investigate their computational advantages.

The following is the list of the claims that are defended in the present dissertation in order to establish this framework named Embodied, Evolving Semiosis:

The living organization requires a system of structural perturbation of self-organizing dynamics, to be able to evolve new classifications (cognitive or phenotypical) of its own interaction with an environment.
If the system of structural perturbation is symbolic, then this evolution is open-ended.
Material symbol systems (used for the system of structural perturbation) are constrained in what can be represented in them.
Evidence Sets model cognitive categories which establish a system of structural perturbation of long-term, connectionist memory banks.
Contextual Genetic Algorithms model material genetic systems and their enabling and restraining constraints.

These claims are approached in different ways. a and b are defended by means of a synthetic gathering of evidence from several existing theories. c is argued in the same way as a and b, but is also validated by results from the formal models defined for points d and e, which are implemented computationally. Next, an outline of the organization of the dissertation is given.

Outline

I intend the present work to be organized in a semiotic way with semantic, syntactic, and pragmatic areas made explicit. This way, the problem is explored philosophically, formally, and computationally respectively. I do not expect the three areas to fully support one another. The philosophical part lays out the problem in general terms and proposes conceptual arguments that should stand on their own. The formal parts, can also stand alone since they represent mathematical constructs valid in their own right. In any case, they are proposed as formal tools to deal with certain aspects of the larger philosophical issues. Finally, the computational parts give some pragmatic validation to certain aspects of the formal tools, by creating computational models of the larger conceptual issues as well as practical applications valid on their own. These computational applications, useful for the fields of data-mining and optimization algorithms, offer the desired pragmatic validation of the philosophical positions advanced. In so doing, they show that there are important advantages to be gained from more inclusive, complementary, theories of artificial intelligence and artificial life that acknowledge both self-organization and representation.

The philosophical and conceptual part of the dissertation starts with a discussion of the divisions between representationalism and self-organization. Self-organization is presented within a framework of emergence and of levels of description. The constructivist position is examined in this context. I introduce the notion of selected self-organization as the backbone of the evolutionary constructivist position, and defend the existence of a symbolic dimension as a pragmatic result to increase the effectiveness of selected self-organization. I further discuss how these ideas relate to the study of natural language and evolutionary systems. Following these ideas, I next propose an evolving semiotic conceptual framework for this inclusive form of self-organization with both representational and constructed facets.

With natural language in mind, I develop a mathematical tool based on fuzzy set and evidence theories called evidence set, proposed as a more accurate model of cognitive categorization processes. Evidence sets extend interval valued fuzzy sets to a belief based framework, creating a method of formally modeling the contextual constraints of cognitive categories. Evidence sets are representational artifacts, but are also constrained by subjective belief structures, which are two key elements of evolutionary constructivism. In addition, evidence sets capture all forms of uncertainty recognized in generalized information theory, uncapturable by other set structures. Finally, an extended theory of approximate reasoning is proposed based on set-theoretic operations defined for evidence sets.

With evolutionary systems and artificial life in mind, I discuss the idea of contextual genetic algorithms. These computational models of natural selection are based on the existence of intermediate levels between genotype and phenotype. In other words, genetic descriptions do not encode directly for phenotypic traits, but for the boundary conditions of intermediate dynamical systems which self-organize into a set of phenotypical traits. The indirect encoding of solutions for a particular problem in genetic algorithms is referred to as contextual since the intermediate dynamical systems may depend on inputs other that just the genetic description, such as environmental observables. That is, expression of chromosomes to solutions does not depend solely on genetic information, but also on the system's context. Indirect genetic encoding is not only a more biologically correct model of genetic natural selection, but it also allows the evolution of different solutions from the same descriptions, which is important for adaptation, and additionally yields tremendous genetic information compression. Furthermore, conceptually, the marriage of selection and self-organization is the crux of evolutionary constructivism in evolutionary systems theory.

In order to validate evidence sets and contextual genetic algorithms as relevant models, I explore them computationally in a number of problem areas. Evidence sets are utilized in the development of a search method which acts on several relational databases. This search is based on the reduction of uncertainty stemming from conflicts between the information stored in the various databases which define several contexts. Contextual genetic algorithms are utilized in two distinct models. The first a model of RNA editing which shows that environmental factors can control genetic translation ontogenetically. The second an indirect encoding scheme based on fuzzy logic designed to attain important information compression of genetic descriptions, which is validated in the evolution of neural networks and cellular automata. Both of these models show how the specific materiality of evolutionary systems, or embodiment, both constrains and enables emergent, evolutionary, classification, which is the thrust of evolutionary constructivism.

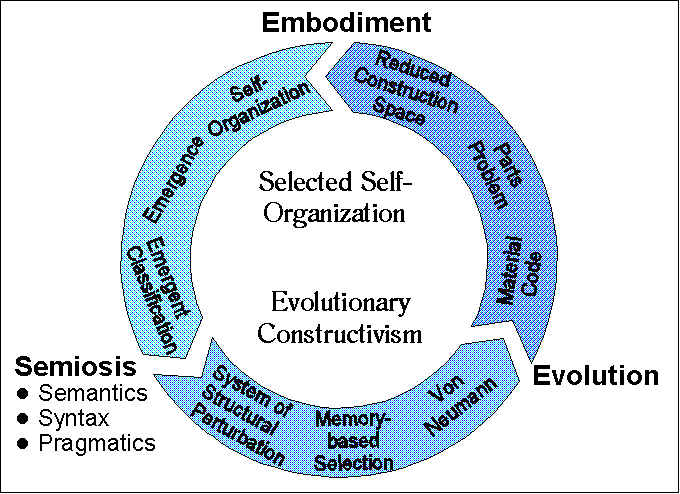
The general layout of the dissertation is organized according to figure 1, where chapter 2 refers to the philosophical discussion of evolutionary constructivism and selected self-organization, chapters 3 and 4 refer to the mathematical discussion of evidence sets and contextual genetic algorithms, chapter 5 refers to the computational models developed, and chapter 6 refers to the final discussion of all the issues discussed before. The following table condenses the organization of the present work.

Topics by Chapter
Chapter 2	Selected Self-Organization and Evolutionary Constructivism	Biological and Cognitive Systems Require Both Self-Organization and Symbolic Representation.
Chapter 3	Evidence Sets and Cognitive Categorization	The ideas of chapter 2 are explored mathematically to deal with the modeling of cognitive categories, which are defined as temporary, subjective constructions grounded in several contexts. Evidence Sets are extensions of Fuzzy Sets defined to better simulate cognitive categories within a logic of belief that captures conveniently all forms of uncertainty recognized
Chapter 4	Contextual Genetic Algorithms	The ideas of chapter 2 are explored formally to deal with the modeling of Natural Selection seen as a process that is both dynamic (material) and symbolic (representational)
Chapter 5	Computer Applications	Practical results are obtained by using the concepts of chapters 3 and 4 to relational databases and evolutionary computation algorithms
Chapter 6	Embodied, Evolving Semiosis: Discussion	The results from chapter 5 are discussed by emphasizing the shortcomings of purely computational models of the ideas defended in chapter 2

Application Areas

The problem areas discussed in this dissertation pertain broadly to the areas of cognitive science, evolutionary systems, and information technology. In particular, to fuzzy logic and evidence theory, as well as evolutionary and adaptive computation and self-organizing systems. The mathematical structures developed have applications to artificial intelligence, reliable computation, relational databases, artificial life, and modeling and simulation. The computational models created have implications for Data Mining, Fuzzy Logic, Genetic Algorithms, Neural Networks, and Cellular Automata.

CHAPTER 2

SELECTED SELF-ORGANIZATION AND EVOLUTIONARY CONSTRUCTIVISM

1. Selected Self-Organization⁽²⁾

1.1 Self-Organization

Self-organization is seen as the process by which systems of many components tend to reach a particular state, a set of cycling states, or a small volume of their state space, with no external interference. All the mechanisms dictating its behavior are internal to the system: self-organization as opposed to externally imposed organization. Thus, it is reasonable to further demand that for a system to observe self-organizing behavior, its order cannot be imposed by special initial conditions, which would amount to a special creation. Therefore, to guarantee that a system is self-organizing, we start it with random initial conditions and see if it attains the desired order, or attractor behavior.

Thus, self-organizing behavior is the spontaneous formation of well organized structures, patterns, or behaviors, from random initial conditions. The systems used to study this behavior computationally are referred to as dynamical systems or state-determined systems, since their current state depends only on their previous state. They possess a large number of elements or variables, and thus high-dimensional state spaces. However, when started with some initial conditions they tend to converge to small areas of this space (attractor basins) which can be interpreted as a form of self-organization. Examples of computational dynamical systems are boolean networks and cellular automata. Since such formal dynamical systems are usually used to model real dynamical systems such as chemical networks of reactions, non-equilibrium thermodynamic behavior [Nicolis and Prigogine, 1977], or even mineral osmotic growths [Leduc, 1911; Zeleny, Klir, and Hufford, 1989], the conclusion is that in nature, there is a tendency for spontaneous self-organization which is therefore universal [Kauffman, 1993].

The existence of attractors is identified with the dissipation of some form of energy, therefore, self-organizing structures can only be maintained by a constant flux of energy through them, and are therefore not in equilibrium. These attractors may be chaotic in which case the emergent behavior becomes too disorganized to grasp (disorganized complexity). The behavior of interest is often found in the transition between order and chaos -- edge of chaos-- and classified as a kind of organized complexity [Weaver, 1948; Langton, 1990]. This behavior -- many parts working together to achieve some order -- is also known as synergetics [Haken, 1977].

1.2 Emergent Classification and Constructivism

1.2.1 Cybernetics and Eigenbehavior

The cybernetician Heinz von Foerster [1981] equated the ability of a self-organizing system to classify its environment with the notion of eigenbehavior. He postulated the existence of some stable structures (eigenvalues) which are maintained in the operations of an organization's dynamics [Rocha, 1994b, 1995b, 1996a]. Following Piaget, he observed that any specific instance of observation of such an organization, will still be the result of an indefinite succession of cognitive/sensory-motor operations [von Foerster, 1977]. This reiterated the constructivist position that observables do not refer directly to real world objects, but are instead the result of a cascade of cognitive and sensory-motor operations in some environment/subject coupling. "Eigenvalues represent the externally observable manifestations of the (introspectively accessible) cognitive [operations]". [von Foerster, 1977, page 278, italics added]. Further, "Ontologically, Eigenvalues and objects, and likewise, ontogenetically, stable behavior and the manifestation of a subject's 'grasp' of an object cannot be distinguished." [von Foerster, 1977, page 280]. Eigenbehavior is thus used to define the behavior of self-organizing, cognitive systems, which through the closure of the sensory-motor interactions in their nervous systems, give rise to perceptual regularities as objects [Varela, 1979, chapter 13].

Notice that eigenvalues are specific to the particular cognitive operations and how they recognize observables, that is, to the system's structure and the corresponding dynamics⁽³⁾. Any system, cognitive or biological, which is able to relate internally, self-organized, stable structures (eigenvalues) to constant aspects of its own interaction with an environment can be said to observe eigenbehavior. Such systems are defined as organizationally closed because their stable internal states can only be defined in terms of the overall dynamic structure that supports them. Organizationally closed systems are also informationally open [Pask, 1992], since they have the ability to classify their constructed environment in what might be referred to as emergent representation

1.2.2 Complexity Theory, Emergent Representation, and Emergent Morphology

It is perhaps easier to think about these concepts in the modern terminology of dynamical systems and complexity theory. The coupling of many simple elements into a network allows the establishment of highly recursive dynamical systems which can observe a wide range of attractor behaviors. Kauffman [1993], for instance, has studied in detail the workings of random boolean networks and their attractor behavior ranges, showing that boolean networks can be made equivalent to most other computational models of self-organization such as cellular automata.

An eigenvalue of an organizationally closed system can be seen as an attractor of a self-organizing dynamical system. The global "cooperation" of the elements of a dynamical system which spontaneously emerges when an attractor state is reached is understood as self-organization [von Foerster, 1960; von Foerster and Zopf, 1962; Ashby, 1962; Haken, 1977; Prigogine, 1985; Forrest, 1991; Varela, Thompson and Rosch, 1991; Kauffman, 1993]. The attractor behavior of any dynamical system is dependent on the structural operations of the latter, e.g. the set of boolean functions and connections in a boolean network. Speaking of an attractor makes sense only in relation to its dynamical system, likewise, the attractor landscape defines its corresponding dynamical system. Furthermore, attractor values can be used to refer to observables accessible to the self-organizing system in its environment, and thus perform environmental classifications (e.g. classifying neural networks). This classification capacity was identified in the cybernetic terminology as eigenbehavior. It is also the crux of the constructivist position [Glanville, 1981]. Not all possible distinctions in some environment can be "grasped" by the self-organizing system: it can only classify those aspects of its environment/sensory-motor/cognitive interaction which result in the maintenance of some internally stable state or attractor (eigenvalue). In other words, not everything "out there" is accessible; only those things that a particular physiology can construct with the stabilities of its own dynamics are.

A classifying self-organizing system is autonomous if all structural processes that establish and sustain its dynamics are internally produced and re-produced over and over again. Autonomy was previously referred to as organizational closure. A computational neural network by itself can classify an environment, but the processes (e.g. a backpropagation algorithm) that make it improve its classifying ability are external to the network. In this sense, the network itself is not autonomous, though the network together with the algorithm that changes its structure may be argued to be. It is precisely the ability of an autonomous system to change its structure in order to better classify a changing environment that defines emergent representation. For a classifying self-organizing system to change its classification ability, structural changes must be performed to alter its attractor landscape (this point is developed ahead). When the structure responsible for a given dynamics is changed, we obtain a new environmental classification (e.g. weight changes in a neural network).

Similarly, living organisms in order to adapt to their environment must be able to change the structure that establishes their own dynamic morphology. It is indeed a similar problem if we regard evolution as a search through a space of possible morphologies. In this case, living organisms must come up with mechanisms for evolving appropriate morphologies for a given environment: emergent morphology. This can be seen as the problem of classification of a morphological space given a certain changing environment, as much as emergent representation is a problem of classification of a space of cognitive representations given a certain changing environment. Natural selection is the living organism's method of structural (genetic) perturbation of self-organizing networks of components. Computational models of this emergent morphology are often based on boolean networks standing for genetic regulatory networks [Kauffmann, 1993], which can be coupled to genetic algorithms [Dellaert and Beer, 1994; Packard, 1988]. In these models, the structure of the boolean network (connections, functions and so on) is changed by the genetic algorithm, leading to different dynamic behavior which in turn stands for different morphologies, appropriate to a problem specified by the genetic algorithm's fitness function. These morphologies self-organize from and are emergent to the boolean network's dynamics, and can be regarded as the classification of an appropriate dynamic configuration for the given selective pressures.

The process of obtaining novel classifications of an environment, by an autonomous self-organizing system, can be referred to as emergent classification. Emergent because it is the result of the local interaction of the basic components of the self-organizing system and not from a global controller. This bottom-up definition of emergence [Langton, 1989] is generally accepted in artificial life and connectionist artificial intelligence as the guiding conceptual framework of models of life and cognition. In the following, I will refer to systems that are capable of emergent classification as complex systems. In section 1.3 I attempt to better specify the concept of emergence.

1.2.3 Self-Organization and Constructivism

Let me now make the connections between the terminologies of second-order cybernetics and complexity theory regarding self-organizing systems explicit by presenting figure 1. This relationship may be taken in some quarters as commonsensical, since most of the cybernetic principles of self-organization as defined by von Foerster and other participants of his program of research at the Biological Computer Laboratory in Urbana, Illinois in the 1960's and 1970's, were proposed within larger philosophical frameworks. In any case, the empirical basis for those theories depends on material and computational systems with the self-organizing characteristics outlined above. It is this empirical foundation of self-organization that I am exploring here, and not the related higher level interpretations of eigenbehavior. The single philosophical issue that I intend to pursue is that of the dependence of an autonomous system's environmental classification on its own dynamics, usually referred to as constructivism.

Autonomous systems must construct their reality by using stable structures internally available. Objects are constructed by peculiarities of cognitive operators (the maintenance of stable structures) and are not accessible through a direct representation of real world categories. Constructivism, the philosophical cornerstone of second-order cybernetics, does not merely entail the idea that objects are not accessible but that objects are constructed by cognition and constitute its basic building blocks. Today, most of us agree one way or another with this principle which shall be discussed in more detail in section 2 of this chapter in the context of cognitive science. However, what must still be addressed is how do these stable eigenvalues become eigenbehaviors, in other words, what is the nature of the structural coupling (to use the autopoietic terminology [Maturana and Varela, 1987]) between an autonomous, self-organizing system, and its environment? How do the internally constructed eigenvalues refer to aspects of the environment? How can we increase the variety of eigenbehavior? Can this variety be open-ended?

1.3 Emergence and Levels of Description

There are three levels that need to be addressed when dealing with the notion of emergent phenomena in self-organizing systems, in particular, of emergent classification. First, there is the material, dynamical, substrate, which will be the causal basis for all other levels that we may further distinguish⁽⁴⁾. Second, we have the attractor behavior of this dynamics. Finally, we have the (possible) utilization of the set of attractors as referents for some aspects of the interaction of the dynamical system itself with its environment (e.g. the pattern recogntion abilities of neural networks).

1.3.1 Explanatory Emergence

Robert Rosen's concept of emergence defines it as the deviation of the behavior of a natural system from a model of it [Rosen, 1985, 1991, 1995]. Peter Cariani [1989] has developed this notion and renamed it emergence relative to a model.

"Emergence relative to a model, then is the result of the finite and hence incomplete character of all models of the world. At some point in time we can, if we are fortunate, construct a model which will deterministically capture the behavior of the physical system. The behavior predicted by the model will, for some period of time, correspond to the observed behavior of the physical system, because it was constructed to do so. But eventually, if one waits long enough, all physical systems will diverge from their models, but some will diverge before others. Physical systems can thus be sorted out according to whether they will exhibit emergence over some finite observational period." [Cariani, 1989, page 164]

I prefer to see emergence relative to a model as an observer's switching between different models offering different modes of explanation, rather than a temporal mismatch (and thus increasing lack of explanatory power) between a model and the observed phenomena. As Howard Pattee [1978] has pointed out, due to the subject-object or observer-system dichotomy, a given observed phenomenon possesses several modes of description, none of which exhibits full explanatory power. In other words, models of physical phenonoma explain only certain aspects of them, and to increase our understanding of the world we need complementary, at times irreducible, modes of description [Pattee, 1978].

Returning to the issue of self-organizing systems and emergence, we observe that the level of attractor behavior is emergent to the dynamics because it cannot be explained solely by a description of the latter. Stability of dynamical states is not expressed in the language of the interactions between the components of a dynamical system. At this lower level, there is no distinction between a stable and an unstable state, between attractor and transient states. For instance, the transition rules of Conway's game of Life cannot describe what "blinkers" and "gliders" are. Likewise, when the attractor landscape is utilized to classify an environment, a new level is created to define the representations necessary for this classifying function: a semantic relation is created. This self-organizing classification is emergent to the attractor landscape level since the latter can only describe stabilities of the dynamics and not any "standing for" relation with the environment. To continue with the previous example, the level of attractor behavior descibes what a glider or a "glider gun" is in the Game of Life, however it cannot describe streams of gliders as information carriers in a universal computer built out of Life patterns [Poundstone, 1987]. The utilization of a glider as a bit of information requires a semantic relation imposed on the level of attractors.

1.3.2 Semantic Emergence

"We must distinguish the syntactical emergence of symmetry-breaking and chaotic dynamics from the semantic emergence of non-dynamical systems which stand for a referent." [Pattee, 1989, pp. 72-73]

No physical or formal description of the dynamical system and its attractors alone will completely explain the "standing-for", or semantic, dimension [Pattee, 1995a]. In figure 2, this third semantic level is depicted by a triangle whose left corner stands for a dynamic attractor, the right corner represents the world "out there", and the top corner represents the system of representation (denoted by a question mark) by virtue of which an internal attractor can be related to its environment. It is also a system of reference, as the representational link between dynamic attractors and an environment is established in reference to a third component. This system defines a cut between what is internal and external [Medina-Martins and Rocha, 1992] to the system, as Pattee [1995b] (following von Neumann [1966]) puts it, between the "knower" and the "known", that is, it defines an epistemic cut. We have then environmental events and a system's representation of those, by virtue of some representational relation. This triadic relationship is often equated in terms of Peircian semiotics [Salthe, 1995], and shall be explored in section 1.7.

The emergence of level 2 (attractor behavior) from level 1 (dynamics) and of level 3 (classification) from level 2 is based on explanatory emergence defined above as the existence of complementary modes of description. However, the emergence of classification from attractor behavior introduces a more specific form of semantic emergence as it establishes a representational relation between the classifying system and its environment. In the following, I shall argue that this emergent representation does not imply a commitment to open-ended representationalism, where symbols are free to represent everything in the environment of the classifying system. Rather, it implies an evolutionarily grounded constructivist stance.

The hierarchy of modes of description discussed in this section is very dear to systems-theoretic approaches to complex systems [Wuketits, 1990]. It requires a broader view of causality. As discussed before, I maintain that classification is materially caused by the attractor behavior of a particular dynamical system. The emergence of the third level of classification, which can also be referred to as a functional level, is often shown to require a more Aristotelian view of causation where final cause is interpreted as functional or intentional cause [Minch, 1995; Salthe, 1995; Rosen, 1991]. Also, if classifying systems are autonomous, then they change their own dynamical structure in order to accommodate different classification abilities (as it will be explored in detail next). In a sense, we have then a closure of cause and effect. For this reason, some have defended that complex systems require a sort of network or feedback causality [Riedl, 1977, 1984, Wuketis, 1990]. At least, a distinction between functional/informational and dynamical causal systems descriptions must be made [Hooker, 1995]. This is precisely the goal of Pattee's epistemic cut and semantic emergence concepts. Recently, Clark [1996] has similarly defended the necessity of complementary models of description in artificial life and artificial intelligence which succumb to neither a pure dynamical systems, self-organizing, vocabulary nor a pure functional, homuncular⁽⁵⁾, description of classifying systems. It is precisely the necessity of emergence, or different levels of description, that makes systems with emergent classification complex.

1.4 Memory and Selected Self-Organization

"What do complex systems have to be so that they can know their worlds? By 'know' I don't mean to imply consciousness; but a complex system like E. Coli bacterium clearly knows its world. It exchanges molecular variables with its world, and swims upstream in a glucose gradient. In some sense, it has a representation of that world." [Kauffman, 1995, page 336]

"Metaphorically, life is matter with meaning. Less metaphorically, organisms are material structures with memory by virtue of which they construct, control, and adapt to their environment." [Pattee, 1995b, page 24]

Self-organizing systems such as neural networks clearly have the ability to discriminate inputs. Generally, the attractors of their dynamics are used to represent events in their environments: depending on inputs, the network will converge to different attractors. If this ability to classify an environment is implemented by the self-organizing system itself, then we can say that it is an autonomous (classifying) system. As previously stressed, not all possible distinctions in some environment can be "grasped" by the autonomous system: it can only classify those aspects of its environment/sensory-motor interaction which result in the maintenance of some internally stable state (attractor). Another way of looking at this is to say that autonomous systems do not represent their environment, they construct it. Autonomous classification is not open-ended but dependent on a system's dynamics.

1.4.1 Variety of Classification and the Edge of Chaos

Self-organizing approaches to life (biological or cognitive), in particular second-order cybernetics [Pask, 1992], take chaotic attractors as the mechanism which will be able to increase the variety (physiological or conceptual) of self-organizing, classifying, systems. External random perturbations will lead to internal chaotic state changes; the richness of strange attractors is converted to a wide variety of discriminative power. However, for any classification to have survival value, it must relate its own constructed states (attractors) to relevant events in its environment, thus, similar events in the world should correspond to the same attractor basin. Chaotic systems clearly do not have this property due to their sensitivity to initial conditions. Ordered systems follow this basic heuristic. If on the "edge of chaos" Langton [1990], ordered systems may in addition allow for higher information exchange and perhaps more 'clever' (evolvable) categorization mechanisms.

"Organisms and other entities which interact with their worlds are likely to couple to those worlds in such a way that smooth classification occurs, and the world is seen as relatively stable. Then the 'knower' should not be chaotic, nor should its classification, the 'known', be. It is a reasonable guess that both the knowing system and the known world are in the [ordered] regime, perhaps near the edge of chaos. [Kauffman, 1993, page 234]"

Kauffman [1993, page 232] further hypothesizes that "living systems exist in the [ordered] regime near the edge of chaos, and natural selection achieves and sustains such a poised state". This hypothesis is based on Packard's [1988] work showing that when natural selection algorithms are applied to dynamic systems such as boolean networks, with the goal of achieving higher discriminative power⁽⁶⁾, the parameters are changed generally to lead these systems into this transitional area between order and chaos. This idea is very intuitive, since chaotic dynamical systems are too sensitive to parameter changes, that is, a single mutation leads the system into another completely different behavior (sensitive to damage). By contrast, ordered systems are more resilient to damage, and a small parameter change will usually result in a small behavior change which is ideal for smooth adaptation (hill-climbing) in correlated fitness landscapes. However, even though very ordered systems can adapt by accumulation of useful successful variations (because damage does not propagate widely), they may not be able 'step out' of certain areas of their fitness landscapes. It is here that systems at the edge of chaos enter the scene, they are not as sensitive to damage as chaotic systems, but still they are more sensitive than fully ordered systems. Thus, some mutations will accumulate (by causing minor changes) and some others will cause major changes in the dynamics allowing more distant searches in fitness spaces. Simultaneous mutation buffering (to small changes) and dramatic alteration of behavior (in response to larger changes) has been shown to be ideal for evolvability [Conrad, 1983, 1990].

1.4.2. Structural Change and Emergent Classification

Chaotic classifications cannot grasp an ordered interaction with an environment, while point attractors and simple limit cycles may not allow enough behavior change for a good increase in variety. The edge of chaos regime seems to offer a good, intuitive, compromise. However, whatever the regime of a dynamic system, self-organization alone cannot escape its own attractor behavior. A given dynamic system is always bound to the complexity its attractor landscape allows. Even a strange attractor, though undoubtably endowed with a much richer variety of behavior than limit cycles or point attractors, is restricted to a very small volume of the state space of the respective dynamic system. If the classification variety of the self-organizing system is restricted to such small volumes, then the ability to classify a changing environment is severely constrained, indeed, it is minimal.

For a dynamic system to observe genuine emergence of new classifications, that is, to be able to accumulate useful variations, it must change its structure. Creativity, or open-ended variety can only be attained by structural perturbation of a dynamical system. One way or another, this structural change leading to efficient classification (not just random change), has only been achieved through some external influence on the self-organizing system. Artificial neural networks discriminate by changing the structure of their connections through an external learning procedure. Evolutionary strategies rely on internal random variation which must ultimately be externally selected. In other words, the self-organizing system must be structurally coupled [Maturana and Varela, 1987] to some external system which acts on structural changes of the first and induces some form of explicit or implicit selection of its dynamic representations: selected self-organization.

Explicit control of a classifying system's structure would amount to the choice of a particular dynamics for a certain task and can be referred to as learning⁽⁷⁾. Under implicit control, the self-organizing system is subjected to some variation of its structure which may or may not be good enough to perform our task. Those self-organizing systems which are able to perform the task are thus externally selected by the environment to which they are structurally coupled. If reproduction is added to the list of tasks these systems can produce based on their dynamic memories, then we have the ingredients for natural selection: heritable variation and selection.

1.4.3 Distributed Memory

The dynamical approach of von Foerster [1965] to cognition emphasized the concept of memory without a record. By utilizing functionals to change the functions of state-determined systems, von Foerster formalized the idea that memory can be observed in systems which are able to change their own structure and therefore its dynamics and attractor behavior. Today, we name this kind of memory distributed, and refer to the kind of models of memory so attained as connectionist. The categories a distributed memory system classifies are not stored in any particular location, they are nowhere to be found since they are distributed over the entire dynamics established by some network of processes [van Gelder, 1991]. They exist however in the form of attractors which are nonetheless discrete at a higher level of description. Categories are not stored in any particular location of the network, but are identified with particular dynamic attractors, for which we need a new, emergent, level of description. Since classified categories are lumped into the attractor landscape of a dynamical system of many components, they are not merely distributed in the sense of being extended over a number of components, they are in fact superposed in the network of component relationships [van Gelder, 1991]. It is precisely because of this superposition that a new level of description is required, since mere knowledge of component interactions cannot describe the classified categories of a connectionist system. Clark [1993], has discussed in detail how connectionism changed our understanding of cognitive categorization processes. More about cognitive categorization in section 2 of this chapter and chapter 3.

Now, for a self-organizing system to be informationally open, that is, for it to observe emergent classification of its own interaction with an environment, it must be able to change its structure, and subsequently its attractor basins, explicitly or implicitly. Whatever the form of selection, this kind of self-organization must be able to classify its interaction with an environment by utilizing its own distributed memory. For selection to occur we must have some internal vehicle for classification -- there must be different alternatives. The attractor landscape, or eigenvalues, offer these vehicles. However, and this is an important point, selection is ultimately not performed on the memory vehicles themselves, but on what they stand for, not on eigenvalues but on eigenbehavior. It is not the pattern of activation of a boolean network which is selected, but its ability to perform a particular task with repercussions on its environment. In other words, it is not the memory which is selected, but the particular repercussions it will lead the self-organizing system to perform in its environment. In terms of the hierarchy of emergence outlined previously, selection takes place on the representational (informational/functional) level (level 3 in figure 2) -- a selection of semantics.

This form of self-organization can be referred to as distributed memory selected self-organization. Its relying on some system-environment coupling of structure has been stressed most notably within second-order cybernetics and systems research. Maturana and Varela [1987] propose structural coupling as the general mechanism for variety increase, Pask [1976] refers to it as conversation in the cognitive realm. Both of these approaches owe a lot to von Foerster's eigenbehavior notions. More recently, in the realm of complex systems and evolutionary systems theory, Kauffman [1993] and others have relied on the notion of autocatalytic sets which are (structurally) mutable, self-replicating, self-organizing systems with distributed memory, evolvable through natural selection. What is yet to be discussed is the potential of this kind of self-organization for efficient, open-ended variety.

1.4.4 Embodiment

So far I have maintained that eigenvalues or attractors represent the building blocks of any system capable of discriminating its environment through some thus embodied construction. However, eigenbehavior (emergent classification) and its variety increase needs a structural coupling of these eigenvalues with some externally selective environment. This kind of selected self-organization obliges us "to understand perception not just as an interactive dynamical structure, but as a process that arises from a more fundamental embodiment that makes it possible for evolution to create structures that are internally assigned interactive roles." [Etxeberria, 1995].

Perhaps the most important characteristic of this distributed memory selected self-organization is the fact that its specific material dynamics both constructs the classification of the environment and ultimately defines selection. That is, distributed memory cannot classify everything, only those aspects of the environment that create internal stabilities. Also, selection eventually acts on the functional characteristics of the dynamics (desired for some task) and not on memory itself. The consequence of this fact for biological systems is that natural selection (acting on this form of self-organization) is not free to evolve any organism, but it is constrained by the dynamic properties of the materiality of the organisms it acts upon -- evolution with both a self-organizing and selection component. The consequence for cognitive systems, is that what can be classified is also constrained by the particular materiality of the classifying system at stake -- not everything "out there" can be grasped. In other words, the particular self-organizing dynamics of a particular classifying system constrains the universe of its classification. However, we should look into how this process can be made more efficient, and allow for genuine open-ended emergence of variety in classification.

1.5 Descriptions and Symbols

1.5.1 Von Neumann and Description-Based Selection

Von Neumann [1966] defended the idea that a threshold of complexity exists, before which complexity degenerates, and after which complexity can increase in an open-ended fashion. He proposed a self-replicating scheme based on the notion of a memory-stored description (A) that can be interpreted by a universal constructor A to produce A itself. However, to avoid a logical paradox of self-reference, the description, which cannot describe itself, must be both copied (uninterpreted role) and translated (interpreted role ) into the described automaton. This way, in addition to the universal constructor, an automaton B capable of copying any description, , is included in the self-replication scheme. A third automaton C is also included to effect all the necessary manipulation of descriptions. To sum it up, the self-replicating system contains the set of automata (A + B + C) and a description (A + B + C); the description is fed to B which copies it and 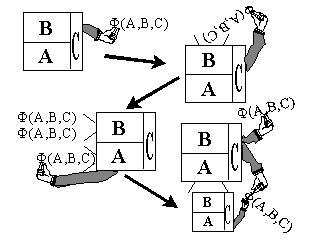to A which constructs another automaton (A + B + C); the copy is then handled separately to the new automaton which together with this description is also able to self-reproduce (figure 3).

As Von Neumann [1966] discussed, if the description of the self-reproducing automata is changed (mutated), in a way so as to not affect the basic functioning of (A + B + C) then, the new automaton (A + B + C) will be slightly different from its parent. Von Neumann used a new automaton D to be included in the self-replicating organism, whose function does not disturb the basic performance of (A + B + C); if there is a mutation in the D part of the description, say D, then the system (A + B + C + D) + (A + B + C + D) will produce (A + B + C + D) + (A + B + C + D). Von Neumann [1966, page 86] further proposed that non-trivial self-reproduction should include this "ability to undergo inheritable mutations as well as the ability to make another organism like the original", to distinguish it from "naive" template-based self-reproduction like growing crystals. Notice that changes in (A + B + C + D) are not heritable, only changes in the description, (A + B + C + D) are inherited by the automaton's offspring and are thus relevant for evolution. This ability to transmit mutations through descriptions cast in separate memories is precisely at the core of the principle of natural selection of modern Darwinism. Through variation (mutation) of memories, populations of different organisms are produced; the statistical bias these mutations impose on reproduction rates of organisms will create survival differentials (fitness) on the population which define natural selection. In principle, if the language of description is rich enough, an endless variety of organisms can be evolved. This is what open-ended emergent evolution means. This point needs to be further elaborated.

1.5.2 Descriptions require a Symbol System

Von Neumann's model clearly does not rely on a distributed but on a local kind of memory. Descriptions entail a symbol system on which construction commands are cast. These commands are not distributed (superposed) over patterns of activation of the components of a dynamic system, but instead localized on "inert" structures which can be used at any time -- a sort of random access memory. By "inert" I mean material structures with many dynamically equivalent states, in other words, the semantic relation, or what the structures are used to refer to, must possess a large degree of arbitrariness so that certain representations are not much more probable than others. In the genetic system, most any sequence of nucleotides is possible, and its informational value is almost completely independent of the particular dynamic behavior of DNA or RNA.

Notice that according to Von Neumann's own formulation, a symbol system utilized for the construction of self-reproducing systems is not an isolated artifact. Rather, in the context of construction, a symbol system entails a set of available parts. That is, construction blueprints are cast on a symbol system whose primitives are a finite set of parts. In the case of self-reproducing automata, these parts are "and", "or" and other logical operators, and in the case of the genetic code the parts are the set of aminoacids (the symbols are codons or sets of 3 nucleotides). It is in this sense that open-ended evolution must be understood. A given material symbol system cannot represent everything, only what its primitive parts can construct. Natural selection is open-ended for any form that can be constructed through folding aminoacid chains.

1.5.3 Parts, Symbols, and Embodiment

This parts problem can be rephrased as one of the aspects of embodiment. A particular materiality is tied to specific construction building blocks. The richer the parts, the smaller the required descriptions, but also the smaller the number of classifiable categories or constructed morphologies. For instance, Von Neumann used simple building blocks such as "and" and "or" gates to build his automaton, which in turn required a 29 state cellular automata lattice and very complicated descriptions. Arbib[1966, 1967] was able to simplify von Neumann's model greatly by utilizing more complicated logical building blocks. Likewise, the genetic system does not need to describe all the chemical/dynamical characteristics of a "desired" protein, it merely needs to specify an aminoacid chain which will itself self-organize (fold) into a functional configuration with some reactive properties. In other words, a given materiality, that is, a given set of parts such as amino acids, provides intrinsic dynamic richness which does not have to be specified by the symbol system on which construction commands are cast [Moreno, et al, 1994] making descriptions much smaller. Embodiment provides this kind of material information compression. The other side of Embodiment, is that it also constrains the universe of possible constructions (universe of open-endedness). Living organisms are morphologically restricted to those forms that can be made out of aminiacid chains through the genetic code, while in principle, a formal symbol system, stripped as it is from any materiality, can describe anything whatsoever. Of course, this 'in principle' is seriously, and easily, constrained by computational limits, as formal descriptions are much larger than material ones. A complete formal description of a protein would have to include all of its physical characteristics from the atomic to the chemical level, while a gene needs only a description of an aminoacid sequence. In chapter 5 I discuss how to incorporate the notion of embodiment in computational models, in order to obtain some form of descriptional information compression.

1.5.4 The Symbolic Advantage

Why then is there an advantage of local memory over distributed memory self-replication? Von Neumann's argument maintains that if we do not have symbolic descriptions directing self-replication, then an organism must replicate through material self-inspection of its parts. In other words, the dynamics must be able to produce copies of itself by template identification of parts existing in its environment. The simplest way would be to have every part of the structure individually heritable. Clearly, as systems grow in complexity, self-inspection becomes more and more difficult [Pattee, 1995a]. The existence of a language, a symbol system, allows a much more sophisticated form of communication. Functional, dynamic structures do not need to replicate themselves, they are simply constructed from physically non-functional (dynamically inert) descriptions. For instance, for an enzyme to replicate itself, it would need to have this intrinsic property of self-replication "by default", or it would have to be able to assemble itself from a pool of existing parts. But for this, it would have to "unfold" so that its internal parts could be reconstituted for the copy to be produced [Pattee, 1995a]. With the genetic code, however, none of these complicated "gimmicks" are necessary: functional molecules can be simply folded from inert messages. This method is by far more general since any functional molecule can be produced from a description, not merely those that either happen to be able to self-reproduce, or those that can unfold and fold at will to be reproduced from available parts. The evolution of distributed memory based self-organizing systems is restricted to this type of trivial (in von Neumann's sense) or through self-inspection reproduction [Kampis, 1991].

The symbol system, with its utilization of inert structures, opens up a whole new universe of functionality which is not available for purely dynamical self-replication. In this sense, it can evolve functions in an open-ended fashion. We can refer to this mechanism as description based evolution. It is the foundation of the neo-Darwinist position and of all genetic based schemes found in evolutionary computation. Its power is obviously immense. It is however at odds with the notions of self-organization depicted previously. For the purely formal von Neumann scheme, all constructions are possible, that is, in principle, there is nothing a formal symbol system cannot describe in a given set of primitive parts. All classifications, all functions, all morphologies can be attained from a finite set of parts by such a mechanism: open-endedness. In contrast, self-organization tells us that a given autonomous system will be able to classify or morphologically achieve only a (small) subset of all possible system/environment configurations; precisely those for which it can construct dynamic stabilities.

It can always be argued that the random access memory the genetic system establishes, is nothing but complicated dynamics, and the symbolic dimension is just the result of our subjective observation. In other words, again the distinction between the levels of attractor behavior and semantic emergence discussed earlier. But why stop there? The same argument may be applied to the dynamic level itself, since it too is constructed by our subjective observations. The genetic dimension has established a new hierarchical level in evolutionary systems [Laszlo, 1987] which allows a greater level of control of the purely self-organizing dynamics. Failing to recognize this emergent symbolic level, does not allow the distinction between self-organizing systems such as autocatalytic networks [Kauffman, 1993], from living systems whose genetic memory does not require larger and larger autocatalytic networks to develop more and more complicated morphologies. Distributed memory self-organization requires more and more complicated gimmicks to increase the complexity of its organization. There is inherited memory, but it is severely constrained as discussed above.

In evolutionary systems this is at the core of the feud between those who claim that natural selection is the sole explanation for evolution and those who stress that other aspects of evolutionary systems, such as developmental constraints, also play an important role. It is no wonder then that the first group stresses the symbolic description, the gene, as the sole driving force of evolution [Dawkins 1976, Dennett, 1995]. While the second group likes to think of the propensities of matter or historical contingencies as being of at least equal importance in evolution [Gould, 1989, Salthe 1985, 1993, Kauffman 1993]. In pragmatic terms, however, most evolutionary theorists, one way or another, will ackowledge that all these factors play important roles [Eldridge, 1995]. Then, is there some conceptual mechanism that will welcome inclusive approaches to evolutionary systems with both description based selection and self-organizing dimensions? Yes, Pattee's [1982, 1995a] semantic closure principle offers such a conceptual avenue. Also, and as we shall see later in chapter 5, in the field of Artificial Life models have been built that incorporate these views with no big fuss.

1.6 Semantic Closure and Open-Endedness

"The symbol vehicle is only a small material structure in a large self-referent organization, but the symbol function is the essential part of the organization's survival and evolution. This autonomous structure-function self-referent organization is what is entailed by my term semantic closure" [Pattee, 1995a, page 14]

The notion of description implies a self-referential linguistic mechanism. A description must be cast on some symbol system while it must also be implemented on some physical structure. Since many realizations of the same symbol system are possible, viewing descriptions only as physical systems explains nothing about their symbolic nature in the control of construction. When Von Neumann's universal constructor A interprets a description to construct some automaton, a semantic code is utilized to map instructions into physical actions to be performed. When the copier B copies a description, only its syntactic aspects are replicated. Now, the language of this semantic code presupposes a set of material primitives (e.g. parts and processes) for which the instructions are said to "stand for". In other words, descriptions are not universal as they refer to some material constituents which cannot be changed without altering the significance of the descriptions. We can see that a self-reproducing organism following this scheme is an entanglement of symbolic controls and material constraints which is closed on its semantics, inasmuch as the semantic code it utilizes is defined by the system itself and not from outside, that is, it relies on autonomous coding. Howard Pattee [1982, 1995a] calls such a principle of self-organization semantic closure.

A given semantically closed system is based on some sort of coding mechanism between inert and functional structures. However, the code and the associated construction are built on some material substrate constraining the whole semantic closure. I can think of two aspects related to this material dependence that are important: the finite number of available parts, and the dynamic, self-organizing, nature of the coded processes.

1.6.1 Finite Symbol-Part System

The symbolic code is defined by a small, finite, number of symbols (e.g. codons in DNA), which can encode a finite number of primitive parts (e.g. aminoacids). Hence, there is a finite number of functional structures which may be constructed with a given set of parts. This defines the representational power of a given symbol system. In other words, the larger the number of possible equally dynamically inert structures, the larger the universe of functionality that can be represented in them. This implies that systems utilizing Von Neumann's scheme of self-replication (biological organisms in particular) cannot evolve any functional structure whatsoever, since the finite properties of a code constrains the domain of evolvable structures. Nevertheless, the number of possible functional combinations attainable even with a small set of symbols and parts (4 and 20 respectively in the DNA-protein code system⁽⁸⁾) is very large, easily beyond computational limits⁽⁹⁾. In this sense, the emergence of functionality is open-ended though not infinite and universal.

1.6.2 Dynamic Part Compounds

"Organisms have hosts of emergent characteristics. In other words, genes interact in a nonlinear way. It is the interaction that defines the organism, and if those interactions, in a technical sense, are nonadditive - that is, if you can't just say that it's this percent of this gene plus that percent of that gene - then you cannot reduce to the lower-level entities, because the nonadditive features have emerged. These features don't exist until you get into the higher level." [Gould, 1995, page 62]

More important for the constraints applied to a selection mechanism based on a Von Neumann type coding system, are the dynamic characteristics of the coded products. A symbol-part system, even with finite number of symbols and parts, is open-ended in the sense discussed above. That is, from coded messages, a trans-computational number of products can be constructed. However, since the products are dynamic and not symbolic structures, they will have different dynamic characteristics (for which they are ultimately selected). Moreover, the messages encoded stand for some arrangement of parts (strings of aminoacids, phrases in natural language) and not just the parts themselves. An arrangement of dynamic structures, however simple, tends to form a complex dynamic compound which will self-organize according to physical laws. This establishes the sort of network causality described earlier in the discussion of self-organizing systems: e.g. folding of aminoacid chains into proteins in the DNA system.

These self-organized, coded, compounds can the interact with one another in many levels of organization which establish the hierarchical nature of evolution [Pattee, 1973; Laszlo, 1987]. Gould [1995], in particular refers to this hierarchy of levels as linked through non-linear relations, meaning that through the network causation of complex dynamic systems we cannot separate individual causes at a lower level from causes at a higher level. This argument is often used to discredit the genetic reductionist stance of Dawkins [1976], as the isolation of genes coding for particular phenotypic traits becomes impossible except for the simplest of cases. Notice that nonlinear behavior is a term often used instead of emergent behavior in complex systems, it is a different way to think about the same phenomenon created by network causality. For instance, the definition of distributed memory as the existence of superposition of representations, as opposed to mere extension of representations across several components, can be rephrased by saying that distributed memory relies on nonlinear representations which are extended across several components of the memory system. If representations were linear, it would mean that, even though extended across components, the percent to which the latter would affect the former would be quantifiable.

In any case, and more relevant here, is to recognize the principle of semantic closure as comprised of symbolic messages that code for self-organizing compounds of material parts. In the computational lingo of Artificial Life, we can say that there is not a linear mapping of coded messages to functional products, rather messages encode dynamic structures which are then left to their own devices as they self-organize. I have referred to this procedure previously as emergent morphology. This concept is developed in chapters 4 and 5 in the context of artificial life and evolutionary computation

1.6.3 Development: Constraints on Evolution

The notion of emergent morphology, as implied by semantic closure, has important implications for evolutionary systems and for cognitive systems. This importance lies on the constraints imposed on the evolution of organisms by natural selection, or the environmental classification performed by cognitive systems. As discussed earlier, self-organizing systems cannot classify or construct everything, as they converge to preferred dynamic pathways defined by their attractor landscape. A given dynamic system has in general only a relatively small number of possible final configurations [Kauffman, 1993]. If complex systems are based on the multi-level hierarchies of interacting dynamic systems built out of initially coded dynamic parts discussed above, then the number of possible final configurations (constructed morphologies or constructed representations) is constrained by this whole hierarchy of dynamic network causality. In other words, not everything can be evolved, as the initial encoded arrangement of parts will have to self-organize under the complicated influence of all sorts of levels of dynamic organization.

The process of reaching a multi-level structure through the self-organization of many dynamic parts is known as development. This process of hierarchical organization has been studied extensively by many in the context of evolutionary systems [e.g. Salthe, 1993; Goodwin, 1994; Buss, 1987]. Under semantic closure, development is seen as an orchestration of dynamic material building blocks and contextual environmental factors, under the initial direction of symbolic controls indispensable for the open-endedness of the process of natural selection according to Von Neumann's model. Some aspects of the notion of development are approached computationally in chapter 5.

1.6.4 Selected Self-Organization with Local Memory

We can then think of semantic closure as a conceptual principle that includes both description based evolution and self-organization, in other words, it implies a description based harnessing of self-organizing structures: selected self-organization with local memory. Figure 4 presents a taxonomy of self-organization dependent on some kind of memory. Notice that distributed memory selected self-organization can achieve plenty of the characteristics of semantic closure I have been discussing, however, without the attributes of local memory, that is, the symbolic dimension of descriptions, we cannot achieve the sort of open-endedness discussed earlier, since construction is not arbitrarily mediated by a code system [Umerez, 1995], but dependent on only those structures that happen to be able to be communicated by template reproduction or self-inspection. This point was discussed in 1.5.

It is here that the emphasis on the symbolic level of open-ended evolutionary systems must be tamed. Strong Darwinism, has emphasized the nature of the symbolic description of living systems. However, semantic closure with its description based selected self-organization is not reiterating this position. The symbolic component of evolutionary systems is stressed, but the material, dynamic, self-organizing characteristics of matter are equally stressed. It is the ultimate inclusive approach which is neither reductionist nor dualist [Pattee, 1995a]. While it is maintained that a purely physical description of dynamics will not explain symbolic function (as several material systems may implement the same function), it is also maintained that different material structures will not have identical domains of potentially evolvable functions. The important idea is that evolution relies both on self-organization and selection, and only those self-organizing systems able to harness their dynamics to obtain a symbolic dimension can have open-ended evolutionary potential.

1.6.5 The Credit Assignment Problem

To wrap up the concept of selected self-organization let me make a summary of the points expressed earlier:

A self-organizing dynamics cannot escape its attractor behavior unless its structure is changed.
To evolve, a self-organizing dynamics needs to accumulate useful variations of structure. In other words, it needs to classify its interaction with its environement. This amounts to the construction of some sort of memory.
Dynamic systems such as boolean networks have distributed memory, which, from an evolutionary perspective, entails a selected construction, or dynamically constrained representation, of their world. Not everything can be classified, only those interactions that lead to dynamically stable behavior and survive in some environment can.
Descriptions (local memory) allow for a more effective form of self-replication based on Von Neumann's scheme.
Von Neumann's scheme of description based evolution does not include dynamics. It is a purely informational, representational, approach. Everything can be classified.
Semantic closure offers a hybrid conceptual approach with both description based (symbolic) controls, and dynamic (self-organizing) constraints. Evolution is the symbolic control or harnessing of self-organization.

Following the previous discussion of emergence, we can see that a pure representational approach, that is, Von Neumann's scheme, utilizes only the third level of description portrayed in figure 2. It disregards all sorts of dynamic constraints that a given material substrate imposes on the classifying function. It formalizes the power of natural selection, which is probably the most important engine of evolution, but it fails to recognize its material constraints which many see as an important part of the evolutionary picture [Gould, 1995]. In fact, these constraints may not just limit the scope of representation, but they may also enable important changes in evolutionary trajectories [Salthe, 1993]. Further, some propose that these dynamic constrains obey universal laws or organization [Kauffman, 1993]. These constraints exist at many levels, from the materiality of specific information carriers, to the mechanisms of symbolic expression (e.g. RNA editing, see chapter 4), to ontogenetic developmental constraints, and all the way to social constraints [Wilson and Sober, 1994].

Semantic closure calls for the so-called credit assignment problem⁽¹⁰⁾. That is, evolutionary structures are subjected to several different controls and constraints, which must be weighted according to their particular relevance in specific organizations. The problem is posed in trying to establish how much of an evolving complex system can be explained by physical laws, self-organization, development and context, historical contingency, and symbolic driven selection. The inclusive nature of semantic closure implies that models of these systems should include as most of these aspects as possible, and not be committed to one single explanatory mode.

1.7 Evolving Semiotics

"The term 'semiotic' goes back to the Greek medical tradition which considered semiotic, embracing diagnosis and prognosis by signs, as one of the three divisions of medicine. The Stoics gave semiotic the dignity of a basic division of philosophy co-ordinate with physics and ethics, and included within it logic and the theory of knowledge. The whole Hellenistic philosophy centered around the semiotic, and in particular the problem of empiricism versus metaphysics was formulated as a problem of the limits of signifying by signs, the Stoics arguing that there were signs ("indicative signs") which could give necessary knowledge about things beyond the limits of observation; the Epicureans holding that while signs gained their signification through experience, some signs (such as 'atom' and 'void') could, though only with probability, refer to what was not capable of direct observation; the Sceptics questioned the whole edifice of metaphysics on the ground that signs could refer only to that which was observable, serving to recall (as "commemorative signs") that which had been observed even though it was not at the moment of reference directly observable." [Morris, 1946, pp. 285-286]

Semiotics concerns the study of signs/symbols in three basic dimensions: syntactics (rule-based operations between signs within the sign system), semantics (relationship between signs and the world external to the sign system), and pragmatics (evaluation of the sign system regarding the goals of their users) [Morris, 1946].

"[...] pragmatics is that portion of the semiotic which deals with origin, uses, and effects of signs within the behavior in which they occur; semantics deals with the signification of signs in all modes of signifying; syntactics deals with combinations of signs without regard to their particular significations or their relation to the behavior in which they occur.

When so conceived, pragmatics, semantics, and syntactics, are all interpretable within a behaviorally oriented semiotic, syntactics studying the ways in which signs are combined, semantics studying the signification of signs, and so the interpretant behavior without which there is no signification, pragmatics studying the origin, uses, and effects of signs within the total behavior of the intepretants of signs. The difference does not lie in the presence or absence of behavior but in the sector of behavior under consideration. The full account of signs will involve all three considerations." [Morris, 1946, page 219]

The importance of this triadic relationship in any sign system has been repeatedly stressed by many in the context of biology and genetics [e.g. Waddington, 1972; Pattee, 1982, 1995a]; in particular, Peter Cariani [1987, 1995] has presented an excellent discussion of the subject. It is a particularly intuitive way of thinking about Selected Self-Organization. Indeed, the three dimensions of semiotics can be mapped to the key aspects of semantic closure. First and foremost, semiotics reminds us that the essential attribute of complex systems with emergent classification is the symbolic, that is, the existence of memory tokens that stand for dynamical configurations. The syntactic dimension can be equated with whatever type of memory tokens⁽¹¹⁾ are utilized to refer to aspects of the complex system's environment (Level 3 in figure 2). The semantic dimension refers to actual (self-organizing) dynamical configurations and their relation to the memory tokens. The pragmatics dimension refers naturally to the selection of the complex system according to its behavior in an environment. Thus, selected self-organization refers to complex systems that observe an embodied evolving semiosis with their environments, which can be open-ended if the natural symbol systems they implement are symbolic and follow von Neumann's scheme (Pattee's semantic Closure). Embodied evolving semiosis is the main concept pursued in this dissertation. It takes the form of selected self-organization in biological systems, and evolutionary constructivism in cognitive systems as discussed in the next section. The implications of its application to AI and AL, which is pursued in chapters 3, 4 and 5, is discussed in chapter 6.

2 Evolutionary Constructivism

In section 1 selected self-organization was presented mostly within the context of theoretical biology, particularly in the study of evolutionary systems. In this section, I attempt to pinpoint more explicitly what evolutionary constructivism stands for in cognitive science, by basing it on the understanding of selected self-organization developed in section 1.

2.1 Material Basis: Selected Self-Organization and Constructivism

Selected Self-Organization relies on the following concepts discussed in section 1:

Self-Organization
Embodiment (materiality, dynamics, environmental interaction)
Classifications as internal stabilities
Constrained Classification power
Hierarchical Development

Semiotic control
Contextual Level integration
Network causality
Selection

Adaptation to an environment
Pragmatics, fitness, consensus
Semantics, function

Constructivism, notably in systems research, has emphasized points 1 and 2 above. The idea that classifications are internally constructed and contextually integrated in a hierarchy of development [Piaget, 1971] is its basic starting point. Classifications are not representations of an environment, but re-presentations generated by cognitive systems in their embodied interaction with an environment [von Glasersfeld, 1995]. Re-presentations refer to the mechanisms by virtue of which a previously constructed classification is re-presented (replayed, re-constructed) from memory given some sensory interaction with the environment. This is understood precisely in the same way as connectionist machines re-create their classifications from previously learned inputs, not so much a direct link to localized memory banks containing fixed representations of the world, but rather an active, dynamic, re-construction of patterns of activation. In fact, constructivism arises hand in hand with the cybernetic fixation on the connectionist machines of McCulloch and Pitts [1943] and von Foerster [1965]. The ability to increase the variety and creation of new re-presentations relies on psychological development primordially based on physiological primitives [Piaget, 1971; Medina-Martins and Rocha, 1992], which progressively generate hierarchies of re-presentations that can be accessed by the structural coupling of cognitive systems to their environments [Maturana, 1979] or through conversations with other such systems [Pask, 1976]. In other words, cognitive systems start with a variety of sensory primitives that are defined by the systems' physiology. This specific embodiment allows a number of interactions with an environment to create internal stabilities (attractors, eigenvalues) used precisely to classify such interactions. All cognitive capabilities are developed from this ability for emergent classification or eigenbehavior, by virtue of a process of learning that works by associating new classifications with existing re-presentations.

2.1.1 Radical Constructivism

Different breeds of constructivism exist. Traditionally, it has been identified with the radical constructivist position of von Glasersfeld [1995], that many fear much more solipsist than it actually is. Mostly because of the practice of its research program (largely implemented in education science), it has left the impression that radical constructivism stands for the sort of relativism found in the deconstructionist, post-modernist, breed of humanities [Derrida, 1977]: the idea that knowledge is personally or socially constructed, with the conclusion that there is no difference between science and humanities, and we can never fully understand our environments since everything is a construction anyway. Alas, this is not the case. Even the most radical of constructivists like von Glasersfeld recognize point 3 of the chart above, that is, they recognize that a level of pragmatics exists that leads constructed re-presentations to refer to relevant events in an environment. However, they tend to either consider cognitive development as the key process to achieve this relevance of classifications, or they are simply not concerned with this aspect of cognition, preferring to work on the construction side of cognition which they believe to be much more relevant.

Radical Constructivism asserts that speaking of representations is an illusion [Von Glassersfeld, page 115, based on arguments by Bickhard and Richie, 1983] that cannot be accepted. The argument is based on the notion of representation as an information-theoretic construct. When a semantic code is established, one can only speak of representation and information transfer if not only the signifiers but also the signifieds are accessible. If one cannot explicitly access all the elements of the set of possible items that one wants to symbolize, then an information channel cannot be defined between the world of signifieds and the language of signifiers, and thus no representational relation can be established.

However, by abandoning the notion of representation as a mapping of internal structures to the world outside, constructivism locks itself inside the autonomy of complex systems it so dearly embraces and restricts cognition to internal coherence models. Psychological development is defined as the process of constructing more and more complicated re-presentations from interaction with an environment comprised of other cognitive agents. What is subsumed in development are the mechanisms of selection of re-presentations which by being selected from outside (socially or ecologically) become effective representations (categorizations) of the classifying system's environment. Constructivism has a problem with accepting explicit external selection, thus the resistance to or downplay of natural selection by the theory of autopoiesis, for instance. As soon as one accepts external, explicit, selection, one must accept a relation (or correspondence) between the world and internal re-presentations which become, effectively, representations (intentionality).

Somehow, cognitive systems construct their classifications of an environment, but misclassifications of an environment may result in ecological or social death, and thus have no survival value. An herbivore in the African savannah should not construct a lion as an edible bush. If a lion triggers such a re-presentation in the herbivore, chances are that it will not survive long. We can say in this evolutionary, pragmatic, sense, that the herbivore misrepresented its environment, an expression which radical constructivism refuses. Such a notion of representation does not have to be seen as an information-theoretic definition. The herbivore's re-presentation of lion, insofar as it allowed the herbivore to survive in the savannah, is effectively a representation of the herbivore's environment where it exists in situated interaction. Such a distinction is possible without explicit access to the environment. A representation is an experiential re-presentation with identifiable repercussions in an environment. It is a pragmatically grounded re-presentation that can be communicated (internally or externally). Evolutionary Constructivism, as developed in more detail ahead, is precisely interested in the study of how communicable (linguistic) representations can establish a more open-ended system of recontextualization of internally coherent re-presentations, that can model cognitive creativity more efficiently.

2.1.2 Physical Constructivism

Heylighen and Joslyn [1992] have proposed a breed of Constructivism named Physical Constructivism which attempts to subsume dynamic, developmental, and evolutionary constraints into a physical dimension. Physicalism tends to reduce the influence of natural selection to laws of dynamics and complexity, stripping it off its pragmatic dimension, and thus preventing any discussion of functionality and representation. If Physical Constructivism merely demands that cognition be understood in terms of the physical processes which manifest cognition, then it is a more reductionist proposal than radical constructivism as proposed by Maturana [1978] or von Glassersfeld [1995]. There is no room for the notion of representation in such a view of cognition: cognitive categories are nothing but the internal, subsymbolic, stabilities of the brain's dynamics, much like the dynamic attractors of artificial neural networks.

2.1.3 Constructionism

Regardless of the problems with constructivism just discussed, the fact is that it brought to the limelight of science and philosophy issues that were being disregarded. Self-organization, embodiment, contextual dependencies, and hierarchical development have only recently been accepted into the core of scientific research, which has been gradually losing its naive realist stance. Most of the basic tenets of constructivism are found on the constructionist theory of learning as proposed by Papert [1991]. It basically asserts two types of construction, an active process in which people actively construct knowledge from their experiences in the world, and it further emphasizes the idea that people construct new knowledge more efficiently when engaged in constructing personally or socially meaningful objects. This approach to education is indeed based on Piaget's ideas, and relies on the basic tenets of constructivism: knowledge is a personal construction of social and ecological interaction. The embodied nature of this interaction is emphasized in the second type of construction used which attempts to maximize learning by physically engaging the participants of a learning experience. Such ideas have been explored by von Glasersfeld and Pask [1976] at least since the 1960's.

2.1.4 Situated Cognition

Similarly, most of the ideas now emerging from embodied artificial intelligence or situated cognition, have strong parallels to constructivist autonomous agents practice [Varela et al, 1992]. Traditionally, AI was concerned essentially with aspects of points 2 and 3 in the chart above. In other words, it relied strongly on models of representation and direct perception of the world. It was mostly preoccupied with functional semantics. The control of its robotic artifacts, for instance, was solely based on the high-level symbol-manipulation of semantic categories.

Artificial Life, mostly through the work of Brooks [1991], whose behavior language replaced the traditional high-level control of robots by a scheme of functional modularization by behavior generating modules, changed all this. Instead of a high-level computation of behavior, the bottom-up (emergentist) self-organization of simpler components produces a variety of behaviors depending on the interaction of a robot with its environment. "Situated" does not mean merely material, but interactive. The material (structural) coupling of the robot with its environment is the source of behavior, and not just the robot control system alone. In other words, the modeling of living and cognitive systems is moved to the dynamics of self-organization of a network of components and its interaction with an environment. Desired behavior is obtained from a hierarchy of simple behavior modules that interact nonlinearly with one another, and through a developmental process of reinforced learning that directs the self-organization of the behavior modules into desired patterns. Mataric [1995] has for instance developed populations of simple social robots that adapt to each other and as a group in this bottom-up fashion.

It can be argued that the behavior modules utilized are still too high level and do not allow the sort of plasticity that living systems observe. Indeed, it is not always obvious how to physically compartmentalize behavior modules: a bird's wing is both an airfoil and engine at the same time [Rosen, 1993]. The sort of behavioral decomposition pursued by Brooks may not offer yet the kind of entailment or network causality found in living organisms [Rosen, 1991; Prem, 1995] which allows for genuine evolution of new behaviors [Cariani, 1992], however, it does mark a very important shift in the practice of AI: the transition from a realist to a constructivist practice of autonomous agents. Cognition is no longer modeled as the creation of universal classifications of the world, but as the embodied interaction of a self-organizing system with its environment. Whichever way situated robots solve a problem, it is done by the construction of their own classifications, given the set of low level components they have available, as they interact with their environment, and not by externally imposed rules.

Furthermore, recent advances in this field, such as Mark Tilden's⁽¹²⁾ research at the Los Alamos National Laboratory, indicate that the descent into simpler material building blocks with rich dynamics, may be able to overcome the criticism that behavioral components are still too high level. Tilden's bots are not programmed with high level behaviors such as the ones traditionally used in situated robotics⁽¹³⁾, in fact they are not programmed at all! They are simply endowed with very dynamically rich components such as legs and antennas, which are nonlinearly connected by a sort of boolean network that converges to limit cycles defining which component is activated and in which sequence. By selecting those that solve intricate tasks by virtue of self-organization alone, Tilden has evolved a very rich fauna of bots capable of the most intricate and interesting behaviors. One shortcoming of his robots, and situated robotics in general, is that they implement solely the dynamic part of selected self-organization, that is, they model self-organization alone. The robots are indeed selected by their behaviors vis a vis a desired task, but for the most part they do not have a mechanism to implement open-ended evolution: the von Neumann scheme. Naturally, this is what situated robotics is trying to move into, though still with many difficulties to solve [Cariani, 1992]. In any case, situated robotics offers an excellent example of constructivist ideas put into practice.

2.2 Realism and Evolutionary Epistemology

As discussed in section 2.1, constructivism is concerned mostly with points 1 and 2 of the selected self-organization bullet chart, that is with Self-Organization and Development. Realism on the other hand is mostly concerned with points 3 and 2: Selection and Development. Selection in the sense that what is important to study is how well a classifying system maps its categories to the real world. In other words, how well it adapts to and performs in its environment, and what is the function and meaning of its categorizations. Realism is concerned with development only to the extent that it facilitates the linear learning of real-world categories, very much like genetic reductionism sees biological development as a cascade of linear transformations under complete genetic control. Realism understands classifications as representations that reflect an external reality.

Very few today pursue a naive realist view of cognition. In fact realism has undergone a series of transformations in order to adapt to systems concepts such self-organization and also to evolutionary thought. Hooker [1995] has reconceptualized realism in terms of Systems Theory and Evolutionary Epistemology sharing many of the motivations pursued by the present work. Being concerned with extreme relativism, Hooker incorporates context sensitivity (social and individual) into the scientific discourse, by regarding cognitive systems (people) as complex adaptive systems, and social processes as the self-organization of many-person systems. Cognitive agency is redefined as the search for increasing performance in a given context (increased fitness). This explicitly allows the introduction of context-dependency. He then views Science as a dynamic self-organizing complex adaptive process, embedded in wider social and biological adaptive systems (society and ecology). Cognition is the process of environmental information collection, given context-specific individual, social, and ecological interactions. Epistemology is thus re-characterized as the construction and re-construction of inquiry procedures invariant across systemic contexts⁽¹⁴⁾ [Ibid, page 4].

In other words, this breed of realism assumes contextual, dynamic, systemic categories as the reality from which invariant procedures can be discovered. The reality of the world is no longer things in themselves, but systemic patterns that are observed across contexts. It can be said that in order to achieve a realist, though contextual, correspondence theory of truth, a pragmatic, systemic, metaphysics needs to be introduced, since cognition is defined as fitness in a given self-organizing system which is assumed a priori. It presupposes complex self-organization as the nature of the world. Once we as cognitive agents interact in the multi-level dynamics of the universe, we can act as if the invariant processes found across a number of contexts were the reality. In other words, there is a consensual element to reality. Science's role is to explore consensually those invariant procedures across the largest number of contexts (individual, social, and ecological).

Now, either one substitutes naive realism for systemic naive realism, in which we believe that the universe is comprised of a number of forms or propensities waiting to instantiate themselves in different material substrates, or this form of realism is no different than constructivism supplemented with an evolutionary pragmatic dimension. Constructivism has always in practice followed an as if, consensual, view of reality [Glanville, 1994]. Given a certain context, for instance the condition of being human which specifies a number of sensory-motor-cognitive primitives, most individual observations in a social environment will be consensually agreed upon by all members of the social group, since, to put it in Hooker's terms, in such a many-person complex system we all share the same evolutionary constraints of fitness and thus our social-ecological reality is essentially the same.

One difference between this approach and the constructivist position is that Hooker seems to take the notions of information and self-organization itself as subject-free observables. He speaks of cognition as environmental information collection to be systematically constructed across contexts, whereas constructivism speaks of information construction as the cognitive primitive. For constructivists, information is by definition always dependent on an observer who constructs it. Evolutionary realism pursues a correspondence theory of truth because it is imbedded in a evolutionary, consensual, systemic, metaphysics. We can speak of truth correspondence between classifications and an environment in the context of natural selection and social-ecological self-organization. As previously stated, this ability to link personal constructed re-presentations to the world was lacking in radical constructivism but can be added by incorporating an evolutionary epistemology dimension. The differences between Hooker's evolutionary realism and the evolutionary constructivist position here pursued are essentially based on that the latter does not require information and systemic constructs as pre-existing realities.

2.3 Critical Realism

"Most scientific discourse is not about the natural world but about representations of selected aspects of that world. Our conceptions of what nature is are mediated by our representations of nature in models, which [...] are subject to certain important constraints. Constraints on our best representations of naturally occuring structures and processes mostly reflect historical conditions for the intelligibility of those representations and the experimental procedures we have devised for manipulating them." [Aronson, Harré, Way, 1995, page4].

A related avenue to reconceptualize realism in the light of systems concepts has been pursued by Aronson, Harré, and Way [1995] and named Critical Realism. As indicated in the quote above, it is a position that acknowledges our conception of nature as a mental artifact, which is nonetheless historically and experimentally constrained. It shares many of the ideas defended in Hooker's Evolutionary Realism, namely that instead of studying reality as comprised of isolated substances, it is studied as comprised of systemic types, that is, sets of relationships between substances. These relationships specify the kind of constraints imposed on nature which can be observed and are the basis of a new contextual ontology. Dynamic-type hierarchies [Way, 1991] are used to model such constraints. This way, the old-fashioned realist emphasis on propositional truth is substituted by a theory of verisimilitude of models -- the degree of match or mismatch between models.

Again, a correspondence theory of truth is maintained by accepting a systemic natural kinds metaphysics and scientific pragmatism. "In other words, ontological atomism is replaced by global-ontological relationalism." [Aronson, Harré, and Way, 1995, page 5]. Pragmatism to the extent that truth is the limit of verisimilitude which is consensually, and pragmatically, worked out as the degree of match and mismatch between models.

Both Evolutionary and Critical Realism share some of the goals of Evolutionary Constructivism though emphasizing different approaches. All accept contextual, embodied cognitive construction. While the new Realism extends Realism with the notion of systemic natural kinds, to be recognized in a contextual ontology, the new Constructivism extends Radical Constructivism with an evolutionary, contextual ontological grounding in an otherwise constructed epistemology. Both approaches are now essentially dual. Critical Realism works with a correspondence theory of truth based on pragmatic, contextual, and consensual verisimilitude, but it requires a systemic natural kinds metaphysics, while Evolutionary Constructivism is based on an internal coherence theory of truth, but it requires an evolutionarily pragmatic correspondence truth metaphysics.

The main difference lies on whether or not one is willing to start with the belief that the world is organized according to systemic natural kinds (based on self-organizing principles) in order to establish a contextual correspondence theory of truth. Realists prefer to ground science this way, while constructivists prefer to start only from the embodied construction of reality, working within an internal coherence theory of truth, which is now supplemented with evolutionary pragmatism to allow a practical belief in a contextual, consensual, as if, correspondence theory of truth. That is, Evolutionary Constructivism works to build the largest possible consensus amongst individually constructed epistemologies, which it believes to be selectively grounded in the natural world. Science is the search for those constructions (built with the extended embodiment of measurement devices) which can be consensually agreed by all individually constructing observers.

2.4 Language Theory and Evolutionary Constructivism⁽¹⁵⁾

The increased study of natural language during recent decades is biased toward two schools of thought. On the one hand is a focus on syntax [Chomsky, 1965; Jacobson, 1982], which studies the components of language and their arrangements, and how those arrangements might be determined. More recently evolution, and related biological aspects of language, have been adopted to the Chomskian school [Pinker, 1993]. The second approach, which attempts to describe natural language in purely biological terms, such as Maturana [1979], prefers to see language more as a phenomenon governed by autonomous self-organization (autopoietic) processes, with the relationship of components within a recursive neural network more a focus than the segregated elements of Chomsky's grammar. Semantics precedes syntax as the more revelatory linguistic feature.

Interestingly, while these methodologies seem opposed in fundamental ways, they each share a commitment to deny symbols and metaphors as proper aspects of theory, arguing for the inappropriateness of these language constructs [Varela et al 1991; Bickerton, 1990] due to the difficulty of objectively describing metaphor and symbolic expression because each requires a high level of subjective interpretive engagement on the part of the observer.

In the following it is argued that any language can be described as possessing four determining aspects:

All languages are biologically based on the neurological networks of the brain, thus any language inherits the self-organizing machine of the brain as fundamental to its operations.
All languages are a recreated system of structural perturbations.
The use of language continually re-contextualizes the epistemology of the individual; the act of recontextualization allows a leap from one dynamic state to another.
This recontextualization is inherently symbolic and metaphorical

A language is thus a system of access to the self-organizing machine of the brain, allowing the individual ecology to perturb and reconfigure the existing knowledge states. In other words, it is defended that language, with its symbolic and metaphorical attributes, allows a kind of selection of the dynamic states of the brain ultimately related to a subject's interaction with an environment. In this sense, language liberates the brain from its own, continuous, dynamic behavior and grants it a discontinuous leaping from one dynamic stability to another. This "leaping" opens the door to a much larger universe of meaning, unreachable by pure dynamics alone.

2.4.1 Selected Self-Organization

We know a good deal from ethology, enough to realize that one of the prevalent structuring processes of the animal brain is the propensity to deconstruct observable objects or events and then to respond based upon an assessment of the elemental parts. Lorenz [1981], Tinbergen [1951] and others have painstakingly documented the deconstruction process in bees, birds, and primates. As an example, a goose will 'see' not an egg as it will see elements of an egg such as color, speckled pattern, shape, and size. A goose can be easily fooled into sitting on a nest of wooden eggs with these elements exaggerated (a brighter green, a more perfect ovoid, larger speckles, and the like).

The deconstruction of reality into elements grants obvious and powerful survival potential: an animal will not be focused on one specific egg, but can 'interpret' all eggs within the selected for categorical constraints. The elements can vary -- in fact variety of recognizable phenomena is inherent in this process. Events and situations can have different components (a nest in one field will never be identical to a nest in another field years later) but elicit the same survival responses. Categorical flexibility is an optimum trait; responding only to a singular, uniquely 'perfect' egg would lead to extinction.

The self-organizing or connectionist paradigm in systems research and cognitive science, has rightly emphasized these characteristics of mental behavior. A given dynamics, say the neuronal interactions of the brain, will converge to a number of attractor states. Such a dynamic system will then utilize these attractors to categorize its own interactions with an environment. This emphasizes the constructivist position that a cognitive agent is not free to categorize all aspects of its environment but only those for which it can construct internal stabilities according to the dynamic characteristics of its particular embodiment, as previously discussed in this chapter. The ability to relate internal stabilities to environmental interactions has been referred to as emergent classification in section 1. It has lead to the idea of memory without record [von Foerster, 1965] and that symbols are not necessary to explain cognition which is inherently subsymbolic [Varela et al 1991]. In applied domains, we have seen the emphasis turn to connectionist machines which classify their environment by manipulation of a network's attractor landscape.

Clearly, these self-organizing systems, if not chaotic, will classify similar events in their environments to similar attractor points of their dynamics: the categorical flexibility observed above. However, to effectively deal with a changing environment, systems capable of relating internal stabilities to environmental regularities, must be able to change their own dynamics in order to create new basins of attraction for new classifications . In other words, the self-organizing system must be structurally coupled to some external system which acts on the structure of the first inducing some form of explicit or implicit selection of its dynamic representations, this was referred to as selected self-organization in section 1. In the biological realm, this selection is implicitly defined by surviving individuals in varying (genetic) populations, while in the cognitive realm we may have some form of explicit selection referred to as learning. A simple example in an applied domain, would be an external algorithm for selecting the weights (structural perturbation) of a neural network in order to achieve some desired classification.

2.4.2 Improving Structural Perturbation

A relevant question at this point is how effective can this structural perturbation get? Connectionist machines can only classify current inputs, that is, they cannot manipulate their own distributed records. Structural change can alter their classification landscape, but we do not have a process to actually access a particular category at any time, except by re-presenting the inputs that cause it to the network. As discussed in section 1, something similar happens at the biological level. If living systems were purely dynamic, then reproduction would have to rely on components that could replicate themselves in a template fashion, or components that could unfold and fold at will so that copies could be made from available elements. In other words, if life did not have a symbolic dimension in DNA, it would be restricted to those proteins and enzymes that could reproduce in a crystal-like manner, or that could unfold to be reconstructed from available amino acids, and then refold to their original form.

Indeed, DNA introduces a novel dimension to living systems which allows them to construct any protein from a genetic description, and not only those that can self-reproduce in the above described senses. This way, DNA introduces a kind of random access memory so that living systems have access at any time to the blueprints of their own construction. This ability liberates living systems from purely localized interactions; biological reproduction is not restricted to template reproduction as the genetic, localized, descriptions can be communicated much more effectively from generation to generation, as well as to different parts of organisms.

It can always be argued that the random access memory the genetic system establishes, is nothing but complicated dynamics, and the symbolic dimension is just the result of our subjective observation. However, the argument is also extendable to the dynamic level itself, since it too is constructed by our subjective observations. Ultimately, all models are subjective. Having accepted this, we can now go our way trying to establish models and explanations that can be consensually agreed by most. As Pattee [1982, 1995a] points out based upon the work of von Neumann (described in section 1), the genetic dimension has established a new hierarchical level in evolutionary systems which allows a greater level of control of the purely self-organizing dynamics. Failing to recognize this emergent symbolic level, does not allow the distinction between self-organizing systems with some dissipative structure such as autocatalytic networks [Kauffman, 1993] (perhaps even hurricanes), from living systems whose genetic memory does not require larger and larger autocatalytic networks to develop more and more complicated morphologies.

The point here, is that language has likewise opened up a whole new universe of meaning for cognitive systems, as they can access the dynamics of classification beyond local interactions. That is, communication between individuals, as well as internally, is not restricted to only those things we can "show" or otherwise somehow physically mimic: the displacement of local observations. Language may be, as the genetic system, a method to point to and reach a particular dynamics necessary in a particular context. It may allow a (fairly) random access to an otherwise distributed memory, defining a more sophisticated system of structural perturbation.

2.4.3 Metaphor

We can thus say that the existence and use of a language is extraordinarily transformational. The categorical constraints of, purely classifying, instinct-level self-organization can be accessed and recontextualized through the consensual, willful exercise of a system of perturbations. It is the recognition of the access to and limited control over a previously closed, interior ecology of largely self-organizing processes that more than likely gave rise to the myths, prevalent in all ancient cultures, that language was a gift of the gods and made humans god-like in its acquisition [Cassirer, 1946].

Language is thus seen as a systematic influence in the recontextualization of an existing epistemology that allows for the leap from one dynamic state to another. It is also critically important to note that any language, because it resides upon the neurological structure of the brain as its chief biological processor, is necessarily constrained by the self-organizing machine that it so perturbs and disrupts. I believe that the most efficacious means to explore the constraints and at the same time the leap of dynamic states is precisely in symbols and metaphors, which are properties that must occur as products of open-ended dynamic state transition.

Symbols, metaphor, and analogy recapitulate the ontogeny of a dynamic state through contestation with another, resulting in a new synthesis within the epistemological domains of those states that are consequently re-formed. Metaphor, symbol, and analogy all share the key characteristic of synthesis of apparent and, in more advanced utility, non-apparent elements of objects and events. A metaphor is thus a heightened degree of routine association made remarkable because it involves the juxtaposition of apparently dissimilar phenomena. This contributes significantly to our survival, enabling us to transfer solutions across problems with similar goal structures. In the most advanced stages of brain development, we achieve true system mapping [Way, 1991], far surpassing other species in our capability to transcend perceptual similarity. Discerning correspondence in non-similar phenomena is one of our highest achievements [Holyoak and Thagard, 1995; Henry, 1995].

2.4.4 Constraints and Evolutionary Contructivism

Constraints are integral to this selected cognitive strategy. A language is by nature open ended and capable of infinite combinations, but its semantic value would be null if there were no categorical restrictions. The variety and richness of semantics depends on the tension between the language as a means of leaping dynamic states while constrained by the inherited neurological processes upon which those states reside. Meaning, in large part, emerges from this tension, from the continual intersection of an abstracting system of organization that must relate by nature of its associative propensities to the external world.

The metaphoric/symbolic quality of language production is inevitable because meaning must be constructed from the associations of often disparate elements and events. To say language or its component words are purely 'representational' misses a critical point: words cannot represent singular objects or events without recourse to a variety of associations. Essentialism is impossible in linguistic constructs. On the other hand, some cognitive categories must relate to the external world, or an organism would not efficiently categorize (and thus survive in) its environment, in other words, the construction of categories must be evolutionarily, and consensually, viable.

Evolutionary constructivism calls for an integration of representational, connectionist, and situated, models of cognition, under an evolutionary epistemology framework. Neither open intentionality nor closed construction can alone explain cognition. Representationalism and constructivism must be brought together under an evolutionary model that includes syntax, semantics, and pragmatics. Evolutionary constructivism accepts that cognition is constructed, that is, it is constrained by its own dynamical embodiment and development, but this form of constructivism also acknowledges the pragmatic, functional, necessity of a representational dimension established through environmental selection. In other words, it merely accepts the need for both self-organizing and evolutionary constraints in models of cognitive categories.

Mental categories are certainly constructed by brains, but if the classification power of such categories in a given environment is null, then the biological systems associated with such brains will most probably not survive in the environment they misclassify. This does not mean that cognitive categorization should be seen as open-ended; not at all, a given material system will only be able to classify certain aspects of its environment, those for which it can construct dynamic stabilities. But it must be able to classify well enough in order to survive. An artificial neural network will also not be able to solve any problem, and we will choose different kinds of networks, with different dynamics, to solve different problems. Thus, models of cognitive categorization need to include the contextual influence of dynamic, developmental, and pragmatic (selective) constraints.

Radical constructivism, based as it is on the dynamic and developmental cybernetic explanations of cognition, often seems to either explain away the notion of representation or avoid it altogether. The same trend takes place in connectionist cognitive science. But we also do not have to pursue a naive realist avenue if we wish to study the notion of representation. It does not have to be seen as the syntactic one-to-one mapping of real world categories to brain categories. Quite the contrary, evolutionary constructivism sees representation as emerging from several dimensions that are mutually constraining: dynamics, development, and pragmatics. The representational aspects of categories have to do with the existence of a pragmatic (selective) dimension. But representation is also constrained by the dynamic and developmental dimensions. It is a truly inclusive approach. In Chapter 3, the problem of Cognitive Categorization is approached in this light, and it is modeled by the introduction of a mathematical structure named Evidence Set.

CHAPTER 3

EVIDENCE SETS: CONTEXTUAL CATEGORIES⁽¹⁶⁾

1. Cognitive Categorization

"Most of our words and concepts designate categories. [...] Categorization is not a matter to be taken lightly. There is nothing more basic than categorization to our thought, perception, action, and speech. Every time we see something as a kind of thing, for example, a tree, we are categorizing. [...] An understanding of how we categorize is central to any understanding of how we think and how we function, and therefore central to an understanding of what makes us human". [Lakoff, 1987, pages xiii, 5, and 6]

Categories are bundles of concepts somehow associated in some context. Cognitive agents survive in a particular environment by categorizing their perceptions, feelings, thoughts, and language. The evolutionary value of categorization skills is related to the ability cognitive agents have to discriminate and group relevant events in their environments which may demand reactions necessary for their survival. If organisms can map a potentially infinite number of events in their environments to a relatively small number of categories of events demanding a particular reaction, and if this mapping allows them to respond effectively to relevant aspects of their environment, then only a finite amount of memory is necessary for an organism to respond to a potentially infinitely complex environment. In other words, only through effective categorization can knowledge exist in complicated environments.

Thus, knowledge is equated with the survival of organisms capable of using memories of categorization processes to choose suitable actions in different environmental contexts. It is not the purpose here to dwell into the interesting issues of evolutionary epistemology [Campbell, 1974; Lorenz, 1971]; I simply want to start this discussion by positioning categorization as a very important aspect of the survival of memory empowered organisms. Understanding categorization as an evolutionary (control) relationship between a memory empowered organism and its environment, implies the understanding of knowledge not as a completely observer independent mapping of real world categories into an organism's memory, but rather as the organism's, embodied, thus subjective, own construction of relevant - to its survival - distinctions in its environment. This is the basis for the evolutionary constructivist position discussed in chapter 2.

Since effective categorization of a potentially infinitely complex environment allows an organism to survive with limited amounts of memory, we can also see a connection between uncertainty and categorization. George Klir [1991] has argued that the utilization of uncertainty is an important tool to tackle complexity. If the embodiment of an organism allows it to recognize (construct) relevant events in its environment, but if all the recognizable events are still too complex to grasp by a limited memory system, the establishment of one-to-many relations between tokens of these events and the events themselves, might be advantageous for its survival. In other words, the introduction of uncertainty may be a necessity for systems with a limited amount of memory, in order to maintain relevant information about their environment. Thus, it is considered important for models of human categories to capture all recognized forms of uncertainty.

Lakoff [1987] has stressed the relevance of the idea of categories as subjective constructions of any beings doing the categorizing, and how it is at odds with the traditional objectivist scientific paradigms. In the following, I will address the historical relation between set theory and our understanding of categories; in particular, I will discuss what kind of extensions we need to impose on fuzzy sets so that they may become better tools in the modeling of subjective, uncertain, cognitive categories.

1.1 Models of Cognitive Categorization

It is important to separate the idea of a model of cognitive categorization and a model of a category. Though obviously dependent on one another, categories are included in more general models of cognitive categorization and knowledge representation. Agreeing on what the structure of a category might be, is far from agreeing on what the structure and workings of cognitive categorization models should be. It is also a simpler problem. Lakoff [1987], for instance, proposes a theory of knowledge organization based on structures called idealized cognitive models (ICM), which contain categories as their substructures or by-products. Other similar models of knowledge organization exist: schema theory [Rumelhart, 1975], frames with defaults [Minsky, 1975], frame semantics [Fillmore, 1982], Dynamic Type Hierarchies [Way, 1991], etc. These models of knowledge organization vary in some ways; Lakoff's ICM's possess in addition to a propositional structure, a subject-dependent physiological structure, and metaphoric and metonymic mappings; in contrast to, for instance, Minsky's purely propositional frames with defaults.

Though, undoubtedly, the specific model of knowledge organization selected will dictate some of the properties of categories, the particular structure chosen to represent categories in such models does not have to offer an explanation for knowledge organization. All that is asked of a good category representation, is that it may allow the larger imbedding model of knowledge representation to function. For instance, if we use mathematical sets to represent categories, our models of knowledge representation may use set theory connectives and/or they may use more complicated sets of mappings or even introduce connectionist machines to produce the sets [Clark, 1993]. Thus, evaluating sets as prospective representations of categories should be done by analyzing the kinds of limitations they necessarily impose on any kind of model, and not simply models circumscribed to basic set-theoretic operations.

1.2 The Classical View

The classical theory of categorization defines categories as containers of elements with common properties. Naturally, the classic, crisp, set structure was ideal to represent such containers: an element of a universe of observation can be either inside or outside a certain category, if it has or has not, respectively, the defining properties of the category in question. Further, all elements have equal standing in the category: there are no preferred representatives of a category - all or nothing membership.

One other characteristic of the classical view of categorization has to do with an observer independent epistemology: realism or objectivism. Cognitive categories were thought to represent objective distinctions in the real world; say, divisions between colors, between sounds, were all assumed to be characteristics of the real world independent from any beings doing the categorizing. Frequently, this objectivism is linked to the way classical categories are constructed on all-or-nothing sets of objects: "if categories are defined only by properties inherent in the members, then categories should be independent of the peculiarities of any beings doing the categorizing" [Lakoff, 1987, page 7]. I do not subscribe to this point of view; we can use classical categories both in realist or constructivist epistemologies. Even with classical, all-or-nothing, categories, the properties are never considered inherent in the members, there is always something defining the necessary list of properties: the external observer/constructor [Medina-Martins and Rocha, 1992]. The question is who or what is to establish the shared properties of a particular category. A model, where these shared properties are regarded as observer dependent, that is, established in reference to the particular physiology and cognition of the agent doing the categorizing, is built under a constructivist epistemology. If on the other hand, these properties are considered to be the one and ultimate truth of the real world, then the aim is the definition of an objectivist model of reality.

Most modern theories of categorization will include classical categories as a special case of a more complex scheme, which does not imply that some categories are objective and others are subjective. Thus, classical categories have to do with an all-or-nothing description of sets, based on a list of shared properties defined in some model. This external model is indeed built within an objectivist epistemology in the classical approach, but these two aspects of the classical theory of categorization are not necessarily dependent. The chosen structure of categories and the chosen model of knowledge representation/manipulation, which can be realist or constructivist, may be independent concerns when modeling cognitive categorization.

1.3 Prototype Theory and Fuzzy Sets

Rosch [1975, 1978] proposed a theory of category prototypes in which, basically, some elements are considered better representatives of a category than others. It was also shown that most categories cannot be defined by a mere listing of properties shared by all elements. Some approaches define this degree of representativeness as the distance to a salient example element of the category: a prototype [Medin and Schaffer, 1978]. More recently, prototypes have been accepted as abstract entities, and not necessarily a real element of the category [Smith and Medin, 1981]. An example would be the categorization of eggs by Lorenz'[1981] geese, who seem to use an abstract prototype element based on such attributes as color, speckled pattern, shape, and size. It is easy to fool a goose with a wooden egg if the abstract characteristics of the prototype are emphasized.

Naturally, fuzzy sets became candidates for the simulation of prototype categories on two counts: (i) membership degrees could represent the degree of prototypicality of a concept regarding a particular category; (ii) a category could also be defined as the degree to which its elements observe a number of properties, in particular, these properties may represent relevant characteristics of the prototype. These two points are distinct. The first makes no claim whatsoever on the mechanisms of creation and manipulation of categories. It may be challenged, as I will do in the sequel, on the grounds that due to its simplicity, models using it must be extremely complicated. Nonetheless, it does offer the minimum requirement a category must observe: a group (set) of elements with varying degrees of representativeness of the category itself.

Now, the second point goes beyond the definition of a category and enters the domain of modeling the creation of categories. As in the classic case, categories are seen as groups of elements observing a list of properties, the only difference is that elements are allowed to observe these properties to a degree. However, the so called radial categories [Lakoff, 1987] cannot be formed by a listing of properties shared by all its elements, even if to a degree. They refer to categories possessing a central subcategory core, defined by some coherent (to a model or context) listing of properties, plus some other elements which must be learned one by one once different contexts are introduced, but which are unpredictable from the core's context and its listing of shared properties⁽¹⁷⁾. Thus, the second interpretation of fuzzy sets as categories leads fuzzy logic to a corner which renders it uninteresting to the modeling of cognitive categorization. Notice that Rosch herself made a distinction between the notion of category prototypes and the notion of knowledge representation:

"Prototypes do not constitute any particular processing model for categories [...]. What the facts about prototypicality do contribute to processing notions is a constraint -- process models should not be inconsistent with the known facts about prototypes. [...] As with processing models, the facts about prototypes can only constrain, but do not determine, models of representation." [Rosch, 1978, pg. 40]

1.4 Dynamic Categories

As Hampton [1992] and Clark [1993] discuss, the important question to ask at this point is "where do the distance degrees come from?" Barsalou [1987] has shown how the prototypical judgments of categories are very unstable across contexts. He proposes that these judgements, and therefore the structure of categories, are constructed "on the hoof" from contextual subsets of information stored in long-term memory. The conclusion is that such a wide variety of context-adapting categories cannot be stored in our brains, they are instead dynamic categories which are rarely, if ever, constructed twice by the same cognitive system. Categories have indeed Rosch's graded prototypicality structure, but they are not stored as such, merely constructed "on the hoof" from some other form of information storage system.

"Invariant representations of categories do not exist in human cognitive systems. Instead, invariant representations of categories are analytic fictions created by those who study them." [Barsalou, 1987, page 114]

As Clark [1993] points out, the reason for this is that since the evidence for graded categories is so strong, even in ad hoc categories such as "things that could fall on your head" or viewpoint-related categories, "it seems implausible to suppose that the gradations are built into some preexisting conceptual unit or prototype that has been simply extracted whole out of long-term memory." [Ibid, page 93] Thus, we should take the graded prototypical categories as representations of these highly transient, context-dependent knowledge arrangements, and not of models of information storage in the brain. In the following, the extensions of fuzzy sets proposed to model cognitive categories should be understood as such.

As for the modeling of cognitive categorization itself, an attempt to model certain aspects of it is developed with an extended theory of approximate reasoning, which is used on a computational system of database retrieval developed in chapter 5. In section 6, this extended theory of approximate reasoning is developed.

1.5 Fuzzy Objectivism

With fuzzy sets and approximate reasoning Zadeh [1965, 1971] substitutes a classic logic of truth by a logic of degrees of truth: instead of having members of classes/categories which belong or not belong to it, we have members that possibly belong to a category to a certain degree. Lakoff [1987] believes that the utilization of degrees of truth adds nothing to the main shortcoming of classical categories, as they are usually thought of as objective graded degrees that exist in the real world; objectivism is merely replaced by fuzzy objectivism. Now, even if Zadeh's initial formulation of fuzzy sets may have been indeed a realist one, nothing prevents us from using fuzzy sets as representations of categories within a constructivist epistemology. Categories defined by fuzzy sets may represent degrees of prototypicality which may vary according to contexts introduced in imbedding models of categorization processes. In particular, a model may take into account levels of physiological subjectivity as desired by Lakoff [1987]. A computational example of such a model has been developed by Medina-Martins and Rocha [1992; Medina-Martins, Rocha, et al, 1994; Medina-Martins, 1995].

Since fuzzy sets, at least to a degree, can be included in realist or constructivist frameworks, its dismissal as good models of cognitive categories has to be made on different grounds. In the following I will maintain that fuzzy sets are unsatisfactory because they (i) lead to very complicated models, (ii) do not capture all forms of uncertainty necessary to model mental behavior, and (iii) leave all the considerations of a logic of subjective belief to the larger imbedding model, which makes them poor tools in evolutionary constructivist approaches. A formal extension based on evidence theory is proposed next.

2. Mathematical Background

This section is not included, please refer to the postscript version

3. Sets and Cognitive Categorization

3.1 Fuzzy Sets and the Prototype Combination Problem

Whenever fuzzy set models of cognitive categories have been proposed, a model of cognitive categorization or human reasoning has also been included in the package. Zadeh [1975] proposed a theory of approximate reasoning based of fuzzy predicate logic. Gorzaczany [1987] proposed a method of inference in approximate reasoning based on interval-valued fuzzy sets. Turksen [1986] presented a method of concept combination based on the idea that fuzzy sets, when combined, should introduce a second degree level of uncertainty. Bo Yuan et al [1994] also investigate an interval valued fuzzy set approach to approximate reasoning based on normal forms. Atanassov [1986; Atanassov and Gargov, 1989] introduced the concept of intuitionistic fuzzy sets and intuitionistic interval valued fuzzy sets together with a whole set of operators [Atanassov, 1994] leading to yet another form of approximate reasoning. These are some of the available models of fuzzy reasoning based on fuzzy categories.

As previously discussed, fuzzy sets are actually fairly accurate representations of categories simply because they are able to represent prototypicality (understood as degree of representativeness); how the prototype degrees are constructed is, on the other hand, a different matter. Fuzzy sets are simple representations of categories which need much more complicated models of approximate reasoning than those fuzzy predicate logic alone can provide in order to satisfactorily model cognitive categorization processes. Critics [Osherson and Smith, 1981; Smith and Osherson, 1984; Lakoff, 1987] have shown that the several fuzzy logic connectives (e.g. conjunction and disjunction) based on different conjugate pairs of t-norms and t-conorms⁽²³⁾, cannot conveniently account for the prototypicality of the elements of a complex category, which may depend only partially on the prototypicality of these elements in several of its constituent categories and may even be larger (or smaller) than in any of these. This is know as the prototype combination problem.

A complex category is assumed to be formed by the connection of several other categories. Approximate reasoning defines the sort of operations that can be used to instantiate this association. Smith and Osherson's [1984] results, showed that a single fuzzy connective cannot model the association of entire categories into more complex ones. Their analysis centered on the traditional fuzzy set connectives of (max-min) union and intersection. They observed that max-min rules cannot account for the membership degrees of elements of a complex category which may be lower than the minimum or higher than the maximum of their membership degrees in the constituent categories. Their analysis is very incomplete regarding the full-scope of fuzzy set connectives, since we can use other operators [see Dubois and Prade, 1985], to obtain any desired value of membership in the [0, 1] interval of membership. However, their basic criticism remains valid: even if we find an appropriate fuzzy set connective for a particular element, this connective will not yield an accurate value of membership for other elements of the same category. Hence, a model of cognitive categorization which uses fuzzy sets as categories will need several fuzzy set connectives to associate two categories into a more complex one (in the limit, one for each element). Such model will have to define the mechanisms which choose an appropriate connective for each element of a category. Therefore, a model of cognitive categorization based solely on fuzzy sets and their connectives will be very complicated and cumbersome. No single fuzzy set connective can account for the exceptions of different contexts, thus the necessity of a complex model which recognizes these several contexts before applying a particular connective to a particular element.

The prototype combination problem is not only a problem for fuzzy set models, but for all models of combination of prototype-based categories. Fodor [1981] insists that though it is true that prototype effects obviously occur in human cognitive processes, such structures cannot be fundamental for complex cognitive processes (high level associations): "there may, for example, be prototypical cities (London, Athens, Rome, New York); there may even be prototypical American Cities (New York, Chicago, Los Angeles); but there are surely not prototypical American cities situated on the east coast just a little south of Tennessee."[Ibid, page 297] As Clark [1993] points out, the problem with Fodor's point of view, and indeed the reason why fuzzy set combination of categories fails, is that "he assumes that prototype combination, if it is to occur, must consist in the linear addition of the properties of each contributing prototype." [Ibid, page 107] Clark proposes the use of connectionist prototype extraction as an easy way out of this problem. In fact, a neural network trained to recognize certain prototype patterns, e.g. some representation of "tea" and "soft drink", which is also able to represent a more complex category such as "ice tea", "does not do so by simply combining properties of the two 'constituent' prototypes. Instead, the webs of knowledge structure associated with each 'hot spot' engage in a delicate process of mutual activation and inhibition." [Ibid, page 107] In other words, complex categories are formed by nonlinear, emergent, prototype combination.

As Clark himself points out, however, this ability to nonlinearly combine prototypes in connectionist machines is a result of the pre-existence of a (loosely speaking) semantic metric which relates all knowledge stored in the network. It is not a proper metric since it may not follow the triangle inequality, but the kind of distance in which the shortest distance between two stored concepts may not be the straight line, often referred to as semi-metric. In any case, through the workings of the network with its inhibition and activation signals, new concepts can be learned which must somehow relate to the existing knowledge previously stored. Therefore, any new knowledge that a connectionist device gains, must be somehow related to previous knowledge. This dependence prevents the sort of open-ended conceptual combination that we require of higher cognitive processes.

This problem might be rephrased by saying that connectionist devices can only make nonlinear prototype combinations given a small number of contexts. We often use a network to classify, say, sounds, another one images, and so sorth. In their own contexts, each network combines prototypes into more complex ones, but they cannot escape their own contexts. I believe, with Clark, that connectionist machines are nonetheless very powerful, even given these constraints. The approach I am about to follow, is not proposed to be used instead of connectionist devices, but one that may offer a more high-level treatment of the contextual problem in prototype combination. In fact, in chapter 5, a computational model is presented that even though not using connectionist machines (distributed memory), uses networked relational databases that also possess semantic semi-metrics and which can approach this contextual problem.

3.2 Interval Valued Fuzzy Sets

As discussed in the previous section, fuzzy sets have extremely limited abilities to model the combination of prototypical categories. They can only work on very limited contexts, whose categories can be formed from the linear combination of constituent categories. The Introduction of a theory of approximate reasoning based on interval valued fuzzy sets [Gorzaczany, 1987; Türken, 1986] represents a step forward in the modeling of cognitive categorization, as it offers a second level of uncertainty, but it only slightly improves the contextual problem referred above. The membership degrees of IVFS are nonspecific (see section 2.3). This second dimension of uncertainty allows us to interpret the interval of membership of an element in a category as the membership degree of this element according to several different contexts, which we cannot a priori identify.

In particular, Turksen's concept combination mechanisms are based on the separation of the disjunctive and conjunctive normal forms of logic compositions in fuzzy logic. A disjunctive normal form (DNF) is formed with the disjunction of some of the four primary conjunctions, and the conjunctive normal form (CNF) is formed with the conjunction of some of the four primary disjunctions: . In two-valued logic the CNF and DNF of a logic composition are equivalent: CNF = DNF. Turksen observed that in fuzzy logic, for certain families of conjugate pairs of t-norms and t-conorms, we have instead DNF CNF for some of the fuzzy logic connectives. He then proposed that fuzzy logic compositions could be represented by IVFS's given by the interval [DNF, CNF] of the fuzzy set connective chosen [Turksen, 1986]. With IVFS based connectives, Turksen was able to deal more effectively with the shortcomings of a pure fuzzy set approach. In his model, two fuzzy sets are combined into an IVFS. The fuzzy and nonspecific degrees of membership of the elements in the category obtained, can be interpreted as inclusion in a category according to several possible, fuzzy degrees.

Turksen's model simplifies the pure fuzzy set approach since we will find more categories which can be combined into complex categories with a single connective used for all elements of the universal set, though it will not work for all radial categories. The IVFS approach provides a way to acknowledge the existence of contextual nonspecificity in complex category formation, thus producing a more accurate representation of different forms of uncertainty present in such processes. The problem is that categories demand membership values which more than nonspecific can be conflicting. That is, the contextual effects may need more than an interval of variance to be accurately represented. Also, even though IVFS use nonspecific membership, thus allowing a certain amount of contextual variance, the several contexts are not explicitly accounted for in the categorical representation. Section 4 proposes set structures which (i) capture all recognizable forms of uncertainty in their membership representation, (ii) point explicitly to the contexts responsible for a certain facet of their membership representation, and (iii) in so doing, introduce a formalization of belief.

3.3. Set complement and intuitionistic sets

Before I introduce such structures in section 4, a comment should be made regarding Atanassov's [1986, 1994; Atanassov and Gargov, 1989] intuitionistic fuzzy sets and interval valued intuitionistic fuzzy sets. A fuzzy set is defined by a degree of membership in [0,1]. As it was noticed in the discussion of uncertainty forms in section 3.2., fuzziness is identified with the conflict between inclusion and non-inclusion in a set. If an element x of X is included in set A to a degree d, then it is also not included in A to a (1-d) degree; in other words, it is included in the complement of A, to a (1-d) degree. An intuitionistic A set is instead defined by both the degree of membership and the degree of non-membership: , with the restriction: . This idea of intuitionistic set introduces an asymmetry between inclusion and non-inclusion which may be very relevant in the modeling of cognitive categories rich in all sorts of asymmetries. These sets have been successfully extended into IVFS with a whole set of relevant operators, thus Gorzaczany and Türken's mechanisms mentioned before could be endowed with this extra asymmetry. I do not pursue this avenue here, but it may prove to be an extension well worth pursuing.

4 Evidence Sets: Membership and Belief

An alternative way to represent an IVFS A is to consider that for every element x of X, there is a body of evidence (F^x, m^x)defined on the set of all intervals of [0,1], I[0, 1], with a single focal element given by the interval . The basic probability assignment function m^x assumes the value 1 for this single focal element, representing our belief that the degree of membership of element x of X in A is (with all certainty) in the sub-interval I^x of [0, 1]. In other words, our judgement of the (nonspecific) degree of membership, I^x, of x in set A indicates that we fully believe it is correct. Notice that the universal set of the IVFS is X, but the universal set of the body of evidence is the unit interval[0, 1].

It is now clear that an IVFS is a very special case of a more general structure which I refer to as evidence set. An evidence set A of X, is defined by a membership function of the form:

A(x): X B[0, 1]

where, B[0, 1] is the set of all possible bodies of evidence (F^x, m^x) on I[0, 1]. Such bodies of evidence are defined by a basic probability assignment m^x on I([0, 1]), for every x in X (focal elements must be intervals). Notice that [0, 1] is an infinite, uncountable, set, while X can be countable or uncountable. Thus, evidence sets are set structures which provide interval degrees of membership, weighted by the probability constraint of DST. They are defined by two complementary dimensions: membership and belief. The first represents a fuzzy, nonspecific, degree of membership, and the second a subjective degree of belief on that membership, which introduces conflict of evidence as several, subjectively defined, competing membership intervals weighted by the basic probability constraint are created.

4.1 Consonant Evidence Sets

An interesting case occurs when we restrict F^x to consonant bodies of evidence, that is, to a nested structure of interval focal elements: . In this instance we obtain a sort of graded and nested structure of several IVFS (Figure 2), which leads to consonant belief measures:. Instead of using a single interval with maximum degree of belief, to formalize the nonspecificity of the degree of membership of element x of X in a set A, as is the case of IVFS, a consonant evidence set uses several nested intervals (three in the case of Figure 2) with different degrees of belief, stating our graded evidence claims regarding the membership of element x of X in A.

4.2 Non-Consonant Evidence Sets

When F^x is no longer restricted to consonant bodies of evidence, we obtain evidence sets that are a bit more "incoherent", that is, disjoint intervals of membership exist for the same membership degree in the evidence set. In other words, the evidence we possess leads to a conflicting characterization of the membership value of x. Figure 3 shows an example of a non-consonant evidence set.

4.3 Complexity of Computation

Even though evidence sets are more complicated than standard fuzzy sets or IVFS, computationally they are still easier structures than general type 2 fuzzy sets or probabilistic sets. As discussed in section 2.3 IVFS require only an upper a lower value for their interval of membership, which is simpler than defining a probability or possibility distribution on membership degrees. Evidence sets are also interval-based set structures, thus each membership degree needs only to be described by simple intervals and their respective weight. If the number of intervals is kept fairly small, which is expected of human discriminative capacities, the complexity of computation is kept very small. In chapter 5 a computer application using evidence sets is proposed which faced no computational problems associated with the complexity of evidence sets. Indeed, the objects used to implement evidence sets are rather trivial compared to the larger relational database scheme in which they are imbedded.

4.4 Contextual Interpretation of Evidence Sets

"To speak of a prototype at all is simply a convenient grammatical fiction; what is really referred to are judgements of degree of prototypicality." [Rosch, 1978, page 40 second italics added]

In the previous sections, the idea of categories as subjective creations of a cognitive agent doing the categorizing was stressed. It was also discussed how a full representation of uncertainty forms, as well as an adequate accounting of context are necessary attributes of good feasible models of categories. None of the fuzzy set and IVFS approaches to this problem consider, explicitly, the notion of subjective context dependencies. This is so because fuzzy sets do not offer an explicit account of belief in evidence; in other words, we have degrees of prototypicality and not judgements of degrees of prototypicality as Eleanor Rosch required in the previous quote.

The interpretation I suggest for the multiple intervals of evidence sets, in light of the problem of human categorization processes, considers each interval of membership I_j^x, with its correspondent evidential weight m^x( I_j^x), as the representation of the prototypicality of a particular element x of X , in category A according to a particular perspective. In other words, each interval I_j^x represents a particular perspective of the element x of a category represented by an evidence set A. Thus, each element x of our evidence set A will have its membership varying within several intervals representing different, possibly conflicting, perspectives. An IVFS refers to the case where we have a single perspective on the category in question, even if it admits a nonspecific representation (an interval)⁽²⁴⁾.

The ability to maintain several of these perspectives, which may conflict at times, in representations of categories such as evidence sets, allows a model of cognitive categorization or knowledge representation to directly access particular contexts affecting the definition of a particular category, essential for radial categories. In other words, the several intervals of membership of evidence sets refer to different perspectives which explicitly point to particular contexts. In so doing, evidence sets facilitate the inclusion of subjectivity in models of cognitive categorization in addition to the inclusion of the several forms of uncertainty.

"Whenever I write in this essay 'degree of support' that given evidence provides for a proposition or the 'degree of belief' that an individual accords the proposition, I picture in my mind an act of judgement. I do not pretend that there exists an objective relation between given evidence and a given proposition that determines a precise numerical degree of support. Nor do I pretend that an actual human being's state of mind with respect to a proposition can ever be described by a precise real number called his degree of belief, nor even that it can ever determine such a number. Rather, I merely suppose that an individual can make a judgement. Having surveyed the sometimes vague and sometimes confused perception and understanding that constitutes a given body of evidence, he can announce a number that represents the degree to which he judges that evidence to support a given proposition and, hence, the degree of belief he wishes to accord the proposition." [Shafer, 1976, p. 21, italics added]

Shafer's intent captured in the previous quotation seems to follow Rosch's earlier quotation in the context of cognitive categorization. The degrees of belief on which evidence theory is based do not aspire to be objective claims about some real evidence, they are rather proposed as judgements, formalized in the form of a degree. Likewise, Rosch's prototypes are not assumed to be an objective grading of concepts in a category, but rather judgements of some uncertain, highly context-dependent, grading. Evidence sets offer a way to model these ideas since an independent⁽²⁵⁾, unconstrained, membership grading of elements (concepts) in a category is offered together with an explicit formalization of the belief posited on this membership. In a sense, in evidence sets, membership in a category and judgments over membership are different, complementary, qualities of the same phenomenon. None of the other structures so far presented are able to offer both this independent characterization of membership and a formalization of judgments imposed on this membership: traditional set structures (crisp, fuzzy, or interval-valued) alone offer only an independent degree of membership, while evidence theory by itself offers primordially a formalization of belief which constrains the elements of a universal set with a probability restriction.

Regarding the previously discussed connectionist extraction of prototypes, notice that Evidence Sets, as any set structure, have independent, unconstrained membership. Connectionist prototypes are implicitly defined by a semantic metric constraining the elements of the categorizing universe. The existence of such metrics may be very important for cognitive categorization. However, and as previously stressed, Evidence Sets are merely proposed as models of cognitive categories, it is up to the model of cognitive categorization to supply additional constraints such as semantic metrics. As a higher level structure, it is very important that Evidence Sets do not have such constraints a priori, in fact, it is precisely their advantage over connectionist devices which are not flexible enough to allow users to arbitrarily change constraints and contexts on prototype-based categories. Later in this chapter, approximate reasoning methods are proposed which shall be used in Chapter 5 to define a database retrieval system that constrains Evidence Sets with context-specific semantic metrics.

5. Relative Uncertainty and Evidence Sets

This section is not included, please refer to the postscript version

6. Belief-Constrained Approximate Reasoning

This section is not included, please refer to the postscript version

7. Evidence Sets and Evidence Theory

This section is not included, please refer to the postscript version

CHAPTER 4

CONTEXTUAL GENETIC ALGORITHMS⁽³¹⁾

1 Models with both Dynamic and Selective Dimensions

The origin of coded systems with both dynamic and selective dimensions is far from understood. It is in fact the problem of the origin of life. But whether or not we know how coded systems can naturally arise, should not stop us from exploring the dynamics-selection coupling of Selected Self-Organization, as described in chapter 2, in scientific models and computational tools. Especially regarding the latter, we may be able to improve information compression in current evolutionary computation algorithms tremendously by including self-organizing layers between solution encoding and expression.

The study of evolutionary systems is often divided in two camps: those that are concerned with self-organizing properties of dynamical systems, and those concerned with models of genetically driven natural selection. The former often use boolean networks and cellular automata as their computational models, while the latter use genetic algorithms or other forms of evolutionary computation. It is not very common to build models with both dimensions in order to explore the nature of this fundamental coupling. It is precisely the nature of the relationship between memory tokens of the selection engine, and construction parts of the self-organizing dynamics that I wish to explore formally here (figure 1). This relationship is in living systems implemented by the genetic code. In abstract terms, it is the harnessing of dynamic materiality by symbolic memory [Pattee, 1982, 1995a]. To fully explore it, it may be useful to frame the problem in terms of the science of semiotics.

2 Semiotics of Living Organizations

As introduced in section 1.7 of chapter 2, semiotics concerns the study of signs/symbols in three basic dimensions: syntactics (rule-based operations between signs within the sign system), semantics (relationship between signs and the world external to the sign system), and pragmatics (evaluation of the sign system regarding the goals of their users) [Morris, 1946]. We can understand the semiotics of the genetic system if we consider all processes taking place before translation as the set of syntactic operations; the relation between mRNA (signifier) and folded amino acid chains (signified), through the genetic code, as the implementation of a semantic relation; and finally, the selective pressures on the developed phenotypes as the pragmatic evaluation of the genetic sign system. Figure 2, which is adapted from Peter Cariani's [1987] extensive discussion of the semiotics of living organizations, depicts these relationships.

Computational models of evolutionary systems, such as genetic algorithms, explore only small portions of the semiotics of the genetic system scheme as depicted in figure 2, namely the pragmatics axis between genotype and phenotype through a linear code that establishes simpler semantic relations. They do not generally explore the syntax axis or the development portion of the semantics axis (except for a few exceptions in the field of Artificial Life [Kitano, 1984; Dellaert and Beer, 1984].) I feel that the inclusion of a more complete picture of the semiotics of living organisms in computational models, can contribute to a much better understanding of evolutionary systems, as well as the definition of more efficient tools for adaptive systems theory. I will discuss the inclusion of syntax and a more complete developmental semantics separately in the next sections. Let us start by looking into the semiotics of the genetic system in more detail.

2.1 Two Type Symbol System: Contextual Environmental Information

Until now, the semiotics of DNA has been considered to be strictly unidirectional: DNA stands for proteins to be constructed. In other words, the symbolic DNA encodes (through the genetic code) phenotypes with repercussions in some environment. Naturally, through variation and natural selection (pragmatic evaluations) new semantic relations between genes and phenotypes are created which are better adapted to a particular environment. However, real-time contextual measurements are not allowed by this unidirectional semiotics. If in addition to symbols standing for actions to be performed, the genetic sign system is also allowed a second type of symbols standing for environmental, contextual, measurements, then a richer semiotics can be created which may have selective advantage in rapidly changing environments, or in complicated, context dependent, developmental processes. Figure 3 depicts such a sign system. The top plane contains two different types of symbols which are combined in different ways (symbolic operations). Type 1 symbols stand for actions through a code (e.g. the genetic code) and type 2 symbols stand for measurements through a different code which is being hypothesized here.

Notice that code is proposed here as an abstraction referring to the set of mechanisms which will link environmental measurements (context) to type 2 symbols. It is not expected to function as a proper genetic code with clear cut symbols (nucleotide codons standing for aminoacid chains). Jon Umerez [1995] has stressed the importance of a code in any form of evolving semiotics. In simple terms, what I refer to as a code here is any mechanism able to relate "inert" material structures (signifiers) to other material structures with some functional dynamics (signifieds) "by virtue" of a larger organizational closure. In other words, the function of the material signifiers is not dependent on their particular materiality, but on what they are used to refer to for the imbedding, material semantic closure [Pattee, 1995a], as discussed in chapter 1. Leaving pragmatic evaluations (selection) out of the picture momentarily, the semantic closure with two symbol types, which is able to act as well as perform measurements on its environment can be represented by the cube in figure 4. The semiotic triadic relationship is only complete when individual semantic closures are coupled to an environment which ultimately selects (pragmatic evaluation) the most fit amongst these symbol-matter closures (e.g. in natural selection, those that reproduce the most), as depicted in figure 5. In section 4, genetic systems with 2 types of symbols are presented by both discussing the RNA editing system and proposing a formal counterpart.

2.2 Embodiment and Implementation Dependence: Selected Self-Organization

The issue of materiality is extremely important for two reasons: (i) all which can be represented in this evolutionary semiotics is restricted to what can be constructed by the specific, material, semantically closed system in the first place; and (ii) selection is ultimately performed on this specific material organization capable of performing a number of functions in an environment. The conceptual framework put forward by this material, evolutionary, semiotics forces self-organization and selection together as two indispensable dimensions of evolutionary systems as discussed in chapter 1. Selection takes place on particular dynamics, on the other hand, open-ended evolution is only possible through the existence of a symbolic dimension mediated through a code. Moreover, this code must be built out of some materiality that constrains its representation power and which also ultimately defines an organism's ability to construct and discriminate its environment. This last point raises the issue of implementation-independence and multiple realizability [Umerez, 1995]. A semantically closed system is not implementation independent because matter constrains its classification power as well as its evolutionary potential. The second constraint is clear when we realize that two distinct closures which at some point may establish the same representational function, if materially different, will potentially evolve differently given their situated interaction with an environment (see section 2.1.4 in chapter 2). The first constraint is not so clear since we hypothetically allow the idea that two different closures can have the same representational function. However, this equivalence can only be established between formal symbol systems which by definition are not materially constrained and are therefore universal, that is, the set of possible semantic relations is infinite (figure 6). Material symbol systems do not have this property. A coding relation must be formed out of certain available material parts in each domain (e.g. nucleotides and aminoacids in the genetic code), and no semantic relation can escape them (this was discussed as the parts problem in section 1.5 of chapter 2). In the genetic system we can represent any protein, but we cannot represent and construct any other material structure which is not made out of aminoacid chains. Thus, our semiotics is necessarily constrained by matter, not just due to selection pressures, but on account of the parts available for the symbol system itself (figure 7).

Material sign systems are not universal and cannot represent anything whatsoever, but this turns out to be their greatest advantage. The price to pay for the universality of formal symbol systems is complete specificity, that is, full description of its components and behavior. Conversely, material sign systems are based on certain building blocks which do not need a description. For instance, DNA does not need to encode anything other than aminoacid chains, there is no need to include in genetic descriptions information regarding the chemical constituents of aminoacids nor instructions on how to fold an aminoacid chain -- folding comes naturally from the dynamical self-organization of aminoacid chains. Notice how a logical simulation of these genetic mechanisms needs to include all this information that comes for free when the self-organizing characteristics of matter are actually used rather than simulated [Moreno et al, 1994]. This information compression is discussed in section 5 by presenting a formal system of development in Genetic Algorithms based on fuzzy logic. A computer simulation of this material semiotics is developed in chapter 5.

3. Contextual Genetic Algorithms

The essence of Genetic Algorithms (GA's) lies on the separation of the description of a solution (e.g. a machine) from the solution itself: variation is applied solely to the descriptions, while the respective solutions are evaluated, and the whole selected according to this evaluation [Holland, 1975]. A genetic algorithm "is primarily concerned with producing variants having a high probability of success in the environment" [Langton, 1989, page 35]. Nonetheless, one important difference between evolutionary computation and biological genetic systems, lies precisely on the connection between descriptions and solutions, between signifier and signified. In genetic algorithms the relation between the two is linear and direct: one description, one solution. While in the biological genetic system there exists a multitude of processes, taking place between the transcription of a description and its expression, responsible for the establishment of an uncertain relation between signifier and signified, that is, a one-to-many relation.

"The proteins encoded by [DNA] are [...] oxymorphic: their individual shapes are precisely unpredictable. So long as this is true, the genomic language, like our own languages, will not have a logical link between signifier and signified. This will not prevent its being read or understood; rather, it will assure that DNA remains a language expressing as full a range of meanings through arbitrary signifiers as any other language." [Pollack, 1994, p. 70]

In other words, the same genotype will not always produce the same phenotype; rather, many phenotypes can be produced by one genotype depending on changes in the environmental context. If the effects of changing environmental contexts affecting gene expression within an individual can be harnessed and used to it's selective advantage in a changing environment, then we can say that such an individual has achieved a degree of control over its own genetic expression. It is the objective of this chapter to propose computational schemes which may be able to achieve this degree of control.

Genetic algorithms explore the semiotics of the genetic system as depicted in figure 2, solely in its pragmatic dimension and in the coded information portion of its semantic dimension. A GA is defined by a population of symbol strings S (Chromosomes) which encode a population of solutions x to a problem. Variation (e.g. crossover and mutation) is applied to the strings, while the solutions are evaluated regarding some problem. The best chromosome-solution pairs, according to the evaluation preformed by a fitness function, will have more (mutated and crossed over) copies of themselves in the next generation. The fitness evaluation implements the pragmatic dimension, while the encoding of solutions to our problem in descriptional strings implements the coded portion of the semantic dimension. Traditional GA's have a one-to-one mapping between chromosomes and solutions, in other words, there is a direct encoding scheme between genotype and phenotype (figure 8). Code in figure 8 implements the semantic relation: on the upper side we have descriptions (signifiers), and on the lower side solutions (signifieds), which relate to each other linearly.

In order to expand GA's to model more aspects of the semiotics of the genetic system, we can act on both sides of this code. Expanding the upper portion enhances the syntax (e.g by allowing 2 types of symbols), while expanding the lower portion enhances the semantics of GA's with a developmental stage, yielding GA's with indirect encoding and a more complicated syntax (figure 9). Both of these expansions can introduce nonlinear interactions, in particular the extension of semantic relations with a developmental self-organization system such as boolean networks [Dellaert and Beer, 1994] or L-Systems and Neural Networks [Kitano, 1994, 1995] offers the desired coupling of models of self-organization to models of Natural Selection.

The expansion of the syntactic dimension makes GA's more accurate models of the Genetic System which is rich in nonlinear interactions before translation through the genetic code (e.g. RNA Editing). Furthermore, since the systems which implement the development of solutions and the manipulation of chromosomes (symbol strings) can receive inputs other than chromosomes (e.g. environmental observables) genetic transcription and solution development may be dependent on contextual factors. Hence, I refer to these expanded GA's as Contextual Genetic Algorithms (CGA's). In the next sections both of these avenues are pursued separately.

4. Exploring Syntax and RNA Editing

The genetic semiotics described in section 2.1 (figures 3 and 4) expands the syntax of the traditional genetic semiotics of figure 2 by postulating richer symbolic interactions than mere DNA/RNA transcription. If a second type of symbols exists, which operate with genetic messages and in so doing change the latter's encoded meaning, their access to environmental information can provide the genetic system real-time control of genetic expression according to context. This ability would certainly be useful for phenotypical development in changing environments. Some evidence has been presented [Benne, 1993; Stuart, 1993; Simpson and Maslov, 1994; Lomeli et al, 1994] that RNA Editing is used in some genetic systems in different amounts according to different contexts (namely, different stages of a developmental process).

4.1 RNA Editing

The discovery of messenger RNA (mRNA) molecules containing information not coded in DNA, first persuaded researchers in molecular biology that some mechanism in the cell might be responsible for post-transcriptional alteration of genetic information; this mechanism was called 'RNA Editing' [Benne at al, 1986]. "It was coined to illustrate that the alterations of the RNA sequence (i) occur in the protein-coding region and (ii) are most likely the result of a posttranscriptional event" [Benne, 1993, page 16]. The term is used to identify any mechanism which will produce mRNA molecules with information not specifically encoded in DNA. Usually we will have insertion or deletion of particular bases (e.g. uridine), or some sort of base conversion (e.g. adenosine guanisine).

The most famous RNA editing system is that of the African Trypanosomes [Ibid; Stuart, 1993]. The mitochondrial DNA of this parasite, responsible for sleeping sickness, "consists of several dozen large loops called maxicircles and thousands of smaller ones called minicircles." [Rennie, 1993, page 132] At first, the minicircles were assumed to contain no genetic information, while maxicircles were known to encode mitochondrial rRNA. However, the maxicircles were found to possess strange sequence features such as genes without translational initiation and termination codons, frame shifted genes, etc. Furthermore, observation of mRNA's showed that many of them were significantly different than the maxicircles from which they had been transcribed. These facts suggested that mRNA's were edited post-transcriptionally.

It was later recognized that this editing was performed by guide RNA's (gRNA's) coded mostly by the minicircles, the strands of DNA previously assumed to contain no useful information [Sturn and Simpson, 1990; Blum, Bakalara, and Simpson, 1990]. In this particular genetic system, gRNA's operate by inserting, and sometimes deleting, uridines. To appreciate the effect of this edition consider figure 10. The first example [Benne, 1993, p. 14] shows a massive uridine insertion (lowercase u's); the aminoacid sequence that would be obtained prior to any edition is shown on top of the base sequence, and the aminoacid sequence obtained after edition is shown in the gray box. The second example shows how potentially the insertion of a single uridine can change dramatically the aminoacid sequence obtained; in this case, a termination codon is introduced.

It is unclear how exactly gRNA's insert uridines into mRNA's; basically, the shorter gRNA strings base-pair with stretches of mRNA, and at some point will insert a number of uridines [Seiwert and Stuart, 1994]. An interesting aspect of the gRNA/mRNA base-pairing is that it is more general than the Watson-Crick base-pairing found in DNA and RNA, it is more ambiguous since "uracils in mRNA can be specified by either guanine or adenine in gRNA" [Stuart, 1993, page 36]

But even if the precise mechanisms of RNA editing are not yet know, its importance is unquestionable, since it has the power to dramatically alter gene expression: "cells with different mixes of [editing mechanisms] may edit a transcript from the same gene differently, thereby making different proteins from the same opened gene." [Pollack, 1994, page 78] (one-to-many relations). It is important to retain that a mRNA molecule can be edited in different degrees precisely according to the concentrations of editing operators it encounters. Thus, at the same time, several different proteins coded by the same gene may coexist, if all (or some) of the mRNA's obtained from the same gene, but edited differently, are meaningful to the translation mechanism.

If the concentrations of editing operators can be linked to environmental contexts, the concentrations of different proteins obtained may be selected accordingly, and thus evolve a system which is able to respond to environmental changes without changes in the major part of its genetic information (genome size optimization). One gene, different contexts, different proteins. This may be precisely what the Trypanosome parasites have achieved: control over gene expression during different parts of their complex life cycles.

"Space is clearly not a problem for mammalian nuclear DNA, so the [previous] rationale is not so obvious for the [editing mechanisms of mammals]. Also there, however, we see one gene encoding two proteins. In mammalian genomes, gene duplication followed by separate evolution of the two copies would be a more obvious way of producing closely related proteins in regulatable amounts. RNA editing, however, does provide the opportunity to introduce highly specific, local changes into only some of the molecules. [...] It could be reasoned that somehow this would be more difficult to achieve via gene duplication, since independently accumulating mutations would make it harder to keep the remainder of the two sequences identical" [Benne, 1993, p. 22]

Thus, RNA editing may be more than just a system responsible for the introduction of uncertainty (one-to-many relations), but also, and paradoxically, a system that may allow the evolution of different proteins constrained by the same genetic string. In other words, even though one gene may produce different mRNA's (and thus proteins), the latter are not allowed heritable variation since they are always constrained by the gene from which they are edited, and which is ultimately selected and transmitted to the offspring of the organism. We can see RNA Editing, especially in the case of gRNA's, as a case of co-adaption of two distinct systems: the stored genetic information (e.g. maxicircles) and the contextual editors (e.g. minicircles), also stored in DNA, but independent and meaningless to the larger semantic loop of the genetic code (figure 11).

The dependent evolution of one gene and several contexts, as expressed by Rob Benne in the previous quote, may allow the introduction of highly specific, local (contextual) changes, more effectively than the independent evolution of several genes. If all of the different expressions were allowed different genes, they would evolve separately not only increasing the size of the genome, but also, possibly, making it harder to maintain coherent, multicellular, phenotypes as well as coherent developmental processes. For instance, the editing of several genes of the Trypanosoma Brucei is developmentally regulated [Stuart, 1993] which may be of evolutionary advantage for these parasites [Simpson and Maslov, 1994]. Though in the course of evolution editing was partially or completely eliminated in many lineages of eukaryotic organisms containing mithocondria, by reverse transcription of partially edited mRNA's, it may be useful for the development of parasitic adaptations as is the case of the developmental regulation of editing in T. Brucei, because parasites need to survive in several completely different environments which require very different responses from them[Ibid]. The African Trypanosomes for instance, use the famous Tsé Tsé flies as carriers before infecting mammals; both present the parasite with completely different environments that trigger in it very different stages of development, at least in great part through the workings of the RNA editing system.

The role of RNA editing in the development of multicellular organisms has also been shown to be important, Lomeli at al [1994] have discovered that the extent of RNA editing affecting a type of receptor channels responsible for the mediation of excitatory postsynaptic currents in the central nervous system, increases in rat brain development. As a consequence, the kinetic aspects of these channels will differ according to the time of their creation in the brain's developmental process.

We can think of DNA as a set of symbolic descriptions based on two types of symbols: type 1 symbols will be expressed in mRNA molecules and will stand for actions to be performed; type 2 symbols will be expressed in gRNA molecules (or other editing mechanisms) and will stand for contextual observables. RNA editing can be seen as a set of symbolic operations performed with symbols of both types, resulting in symbols of type 1 to be translated into actions by the genetic code. This implements the two type symbol semiotics system described in section 2.1.

4.2 A Formal Model of Genetic Editing

This section is not included, please refer to the postscript version

4.3 Context and Evolutionary Systems

This section is not included, please refer to the postscript version

5. Development and Material Constraints

In chapter 2 (section 1.5.3) I equated the notion of embodiment with von Neumann's parts problem. This aspect of evolutionary systems lies on the semantic area of the semiotics of the genetic system. In figure 2 it is depicted in the bottom part of the semantic relations axis, that is, the development of a phenotype from amino acid chains. Especially in computational realms, we tend to think of the genetic system as a one-to-one mapping of genetic strings to completed phenotypes or solutions to a problem. However, as emphasized earlier (section 2.2 and chapter 1), biological genetic strings encode amino acid strings that will themselves self-organize (fold and subsequently engage in some developmental process) into a final product that is not explicitly genetically encoded -- if it were, genotypes would have to be tremendously larger. This fabulous information compression is achieved by utilizing powerful dynamic building blocks, the amino acids, whose physical characteristics do not require encoding.

To explore these ideas computationally, we need to use genetic algorithms that code for some computational building blocks whose (computational) dynamic characteristics do not require genetic encoding, and which will self-organize into a final solution not explicitly encoded. The self-organization of solutions from encoded descriptions is an instance of the process of emergent morphology/classification as discussed in chapter 1. In the following I discuss some approaches to achieve models of this selected self-organization. I also propose a scheme in which the computational building blocks are represented by fuzzy sets to be implemented in chapter 5.

5.1 Development in Artificial Life

Development refers to those processes taking over an organism once it is reproduced and which are responsible for the transformation of its form. Generally, artificial life models of development are based on Wilson's [1988] ideas: a GA will encode "a production system program (PSP) consisting of a finite number of production (condition-action) rules [...] of the form: X + K_i K_jK_k. The K's stand for cell phenotypes and X represents the local context". [Ibid, page 159]. Basically, the symbolic descriptions of the GA code for a population of "mother cells", or "eggs". These "eggs" code for a specific PSP (a set of production rules) dictating how the "cell" develops into some multicellular aggregate, which is then evaluated for its fitness. The more fit aggregates will have the symbolic description of its "egg" reproducing with a larger probability in the population. These ideas have been used mostly to generate neural networks [Kitano, 1990; Belew, 1993; Gruau, 1992] or more generally sensorimotor control systems [for a good overview see Husbands et al, 1994].

Lately much attention has been posited on evolutionary strategies that bring together self-organizing systems and natural selection inspired algorithms. Particularly in the field of Artificial Life, Kitano[1994], and Dellart and Beer [1994], have proposed GA's which do not encode directly their solutions, but rather encode generic rules (through L-Systems) which develop into boolean networks simulating metabolic cycles. With these approaches, GA's no longer model exclusively selection, but also a self-organizing dimension standing for some materiality. The GA does not search the very large space possible solutions, but a space of basic rules which can be manipulated to build different self-organizing networks. These networks are then started (sometimes with some learning algorithm) and will converge to some attractor behavior standing for a solution of our simulation. Rather than directly encoding solutions, the GA harnesses a space of possible self-organizing networks which will themselves converge to a solution -- emergent morphology.

Usually such indirect encoding schemes for genetic algorithms are based on the encoding of generic rules for developing dynamic systems, e.g. boolean networks [Dellaert and Beer, 1994] or neural networks [Kitano, 1994, 1995], which will themselves self-organize into final solutions. The primary advantage of indirect encoding GA's is the information compression of encoded solutions into smaller chromosomes. The GA does not search the very large space of possible solutions, say, the set of weights of a large neural network (see chapter 5), but a space of generic rules which self-organize into solutions (usually L-Systems that produce large neural networks). Indirect encoding in GA's is an attempt to utilize the advantages of embodiment discussed earlier in a computational realm.

The semiotic genetic system does not encode every detail of the obtained solutions, rather it encodes a development scheme which relies on the pre-existence of rich enough building blocks that do not require a description. In biological systems these building blocks are amino acids whose dynamical characteristics genes do not need to encode as they "come for free" with the laws of matter. In the computational realm, we can ease the chromosomes of a GA from having to describe every detail of the solutions through an indirect encoding scheme. However, some form of that description is unavoidable somewhere else in a computer implementation, since computer programs require full specification by definition. It is therefore important to have as simple as possible a description of the dynamic building blocks for the indirectly encoded GA solutions. If a true computational dynamic system, such as a boolean network, is used, every time a chromosome is decoded into a set of rules to build the network that will self-organize into a solution [Dellaert and Beer, 1994], the network will actually have to be implemented and run for a number of cycles in all its details. Thus at each step of the GA, the evaluation of a chromosome relies on a computationally demanding evaluation procedure that must implement and observe the dynamic behavior of a network, which many times develops into long transient cycles. For this reason I have developed an indirect encoding scheme which utilizes fuzzy sets as representations of the states of dynamical systems presented next.

5.2 Fuzzy Development Programs: Emergent Classification in Contextual Genetic Algorithms

This section is not included, please refer to the postscript version

CHAPTER 5

IMPLEMENTING CONTEXTUAL STRUCTURES FOR DATA MINING

In this chapter the formalisms defined in chapters 3 and 4 are explored computationally. The applications developed pertain to the broad field of data mining. This area of Information Sciences and Machine Learning is dedicated to building computational tools that can help us search and categorize the immense information resources available today. One of the most significant subareas of data mining research is that of knowledge discovery in databases. Particularly with the exponential growth of the Internet, it is becoming harder and harder to effectively search databases without being overwhelmed by a cascade of unrelated results to users' queries. Section 1 of this chapter presents a conversational knowledge discovery system for relational databases that uses evidence sets as categorization mechanisms. Its objective is the definition of a human-machine interface that can capture more efficiently the user's interests through an interactive question-answering process.

Another area of interest to data mining is that of the search of solutions for a problem in very large state spaces. Contextual genetic algorithms (CGA's) with fuzzy indirect encoding are used in two different problems. The first is the search of the appropriate set of weights for a very large Neural Network. The GA is used as a learning algorithm. It is a continuous variable problem. The second problem is the evolution of Cellular Automata rules to solve non-trivial tasks. It is a discrete variable problem. The fuzzy indirect encoding CGA of chapter 4 is shown to deal with such large problems efficiently.

1. Computing Categories in Relational Databases: Linguistic Categories as Consensual Selection of Dynamics⁽³³⁾

The notion of uncertainty, is very relevant to any discussion of the modeling of linguistic/mental abilities. From Zadeh's [1971, 1975] approximate reasoning to probabilistic and even evidential reasoning [Schum, 1994], uncertainty is more and more recognized as a very important issue in cognitive science and artificial intelligence with respect to the problems of knowledge representation and the modeling of reasoning abilities [Shafer and Pearl, 1990]. Engineers of knowledge based systems can no longer be solely concerned with issues of linguistic or cognitive representation, they must describe "reasoning" procedures which enable an artificial system to answer queries. In many artificial intelligence systems, the choice of the next step in a reasoning procedure is based upon the measurement of the system's current uncertainty state [Nakamura and Iwai, 1982; Medina-Martins et al, 1992, 1994]. Now that a theory of evidential approximate reasoning and measures of uncertainty are defined for evidence sets (see chapter 3), we can extend fuzzy data-retrieval systems to an evidence set formulation.

1.1 Nakamura and Iwai's Fuzzy Information Retrieval System⁽³⁴⁾

This section is not included, please refer to the postscript version

1.2 Contextual Expansion With Evidence Sets

In chapter 3, section 3, the construction of prototypical categories from connectionist machines was examined. One of the problems referred was that connectionist machines do not easily allow the treatment of several different contexts in the categories they construct. Each network is trained in a given problem area or context, whose concepts are stored in a distributed manner and for which a semantic semi-metric is established. But one network will not be able to relate a completely novel concept with its semantic semi-metric unless it is retrained in a larger context with expanded training patterns. Similarly, the system described above in 1.1. though not connectionist, observes some of the key characteristics of such systems. In particular, the inclusion of a new concept in its knowledge space, implies the recalculation of the entire set of distances for all concepts related to the new one up to a desired level (n-reachable concepts)⁽³⁶⁾.

Ideally, for both machines with connectionist or relational long-term memory, there should exist a mechanism that bridges information from networks trained in specific contexts. In other words, we would like a mechanism to categorize information stored in different long-term contextual memory banks. It is also desirable that the higher-level, short-term categorization processes may re-shape the long-term memory banks with the history of categorizations. The expansion of the system in 1.1 to an evidence framework achieves precisely that.

1.2.1 Distances from Several Relational Databases: The Extended Long-Term Memory Structure

Consider that instead of one single database (with concepts and properties) we have several databases which share at least a small subset of their concepts (keywords). Since they are linked to different properties, the similarity relation between concepts as defined by equation (1) is different from database to database, and so will the distance semi-metric given by (2). For instance, keyword "fuzzy logic" will be differently related to keyword "logic" in the library databases of a control engineering research laboratory or a philosophy academic department. We may desire however tosearch for materials in both of these contexts. Figure 3 depicts such structure with two different relational databases.

The knowledge space X of this new structure is now the set of all concepts in the n_d included databases. Unlike the knowledge space of the system in section 1.1, that had only one distance semi-metric defined on set X, in this case the system has n_d different distance semi-metrics, d_k, associated with it. Each distance semi-metric is still built with equation (2) for some acceptable level of n-reachable concepts. But since each of the n_d databases has a different concept-property pattern of connectivity, each distance semi-metric d_k will be different. When a concept exists in one database and not on another, its distance to all other concepts of the second database is naturally set to infinity. If the databases derive from similar contexts, naturally their distance semi-metrics will tend to be more similar. This distinction between the several contextual relational memory banks provides the system with intrinsic contextual conflict in evidence.

The ability to relate several relational databases is a very relevant endeavor for data-mining in this age of networked information. Users have available today a large number of networked client-server relational databases, which keep partially overlapping information gathered in different contexts. It is very useful to set up search applications that can relate the several sources of information to the interests of users. Such mechanisms need to effectively group several contextual sources of related long-term memory into temporarily meaningful categories.

1.2.2 Extended Short-Term Categorization

This section is not included, please refer to the postscript version

1.2.3 Document Retrieval

The mechanism of document retrieval is very similar to the one described in 1.1.3, except that the indices given by equations (5), (6) and (7) are adapted for evidence sets. First the evidence set category is simplified to its closest fuzzy set by a process of elimination of nonspecificity and conflict. Basically, the fuzzy membership is defined as the center of all weighted interval focal elements. Once this fuzzy set is obtained (5), (6), and (7) can be used.

1.2.4 Adaptive Alteration of Long-Term Structure

The adaptive alteration of the long-term structure is also essentially equivalent to the one described in section 1.1.4. When concepts tend to be present in short-term learned categories, their relative distance in the long-term relational structure is adaptively reduced. The only difference is that now the long-term structure is divided in several sub-databases. Thus, when two highly activated concepts in the learned category are not present in the same database (each one exists in a different database) they are added to the database which does not contain them, with property counts given by equations (8) and (9). If the simultaneous activation keeps occurring, then a database that did not previously contain a certain concept, will have its presence progressively strengthened, even though such concept does not really possess any properties in this database - properties end up being associated with it through the concept's relations to native concepts of the database. This way, short-term memory not only adapts an existing structure to its users as the system in section 1.1, but effectively creates new elements in different, otherwise independent, relational databases, solely by virtue of its temporary construction of categories.

1.2.5 Categories as Linguistic, Metaphorical, Structural Perturbation

The evidence set question-answering system follows essentially the algorithm presented in section 1.1 except that now the constructed categories capture more of the prototypical effects discussed in chapter 3. Such "on the hoof" construction of categories triggered by interaction with users, allows several unrelated relational networks to be searched simultaneously, temporarily generating categories that are not really stored in any location. The short-term categories bridge together a number of possibly highly unrelated contexts, which in turn creates new associations in the individual databases that would never occur within their own limited context. Therefore, the construction of short-term linguistic categories in this artificial system, implements the sort of structural perturbation of a long-term system of associations discussed in chapter 2, section 2.4. It is in fact a system of recontextualization of otherwise, contextually constrained, independent relational networks.

This transference of information across dissimilar contexts through short-term categorization models some aspects of what metaphor offers to human cognition: the ability to discern correspondence in non-similar concepts [Holyoak and Thagard, 1995; Henry, 1995]. Consider the following example. Two distinct databases are going to be searched using the system described above. One database contains the books of an institution devoted to the study of computational complex systems (e.g. the library of the Santa Fe Institute), and the other the books of a Philosophy of Biology Department . I am interested in the concepts of Genetics and Natural Selection. If I were to conduct this search a number of times, due to my own interests, the learned category obtained would certainly contain other concepts such as Adaptive Computation, Genetic Algorithms, etc. Let me assume that the concept of Genetic Algorithms does not initially exist in the Philosophy of Biology library. After I conduct this search a number of times, the concept of Genetic Algorithms is created in this library, even though it does not contain any books in this area. However, with my continuing to perform this search over and over again, the concept of Genetic Algorithms becomes highly associated with Genetics and Natural Selection, in a sense establishing a metaphor for these concepts. From this point on, users of the Philosophy of Biology library, by entering the keyword Genetic Algorithms would have their own data retrieval system output books ranging from "The Origin of Species" to treatises on Neo-Darwinism - at which point they would probably bar me from using their networked database! The point is, that because of the Evidence Set system of short-term categorization that uses existing, fairly contextually independent relational sub-networks, an ability to create correspondence between somewhat unrelated concepts is established.

1.2.6 Open-Ended Structural Perturbation

Given a large number of sub-networks comprised of context-specific associations, the categorization system is able to create new categories that are not stored in any one location, changing the long-term memory banks in an open-ended fashion. Thus the linguistic categorization Evidence Set mechanism achieves the desired system of open-ended structural perturbation of long-term networked memory. As discussed in chapter 2, open-ended in terms of all the available dynamic building blocks that establish the personal construction of associations. Open-endedness does not mean that the categorizing system is able to discern all physical details of its environment, but that it can permutate all the associative information that it constructs in an open-ended manner. Each independent network has the ability to associate new knowledge in its own context (e.g. as more books are added to the libraries of the prior examples): these are the building blocks. To this, the categorization scheme adds the ability of open-ended associations built across contexts. Therefore, a linguistic categorization mechanism as defined above, offers the ability to re-contextualize lower level dynamic memory banks, as a result of pragmatic, consensual, interaction with an environment. This linguistic consensual selection of dynamics, was identified in chapter 2 as the main idea behind Evolutionary Constructivism as the cognitive version of a theory of embodied, evolving, semiosis.

1.2.7 TalkMine: The Implemented Application

This section is not included, please refer to the postscript version

2. Emergent Morphology and Evolving Solutions in Large State Spaces⁽³⁷⁾

The Contextual Genetic Algorithm (CGA) with fuzzy indirect encoding defined by Fuzzy Development Programs (FDP'S) described in chapter 4 (section 5.2), was applied to two different cases. The first one refers to the evolution of weights for a large neural network; it is a continuous variable problem. The second, refers to the evolution of Cellular Automata (CA) rules for solving non-trivial problems; it is a discrete variable problem.

2.1 Implementation Details

This section is not included, please refer to the postscript version

2.2 Continuous Variables: Evolution of Neural Network Weights

Interesting results have been obtained when using genetic algorithms (GA's) to evolve the weights of a neural network with a fixed architecture. For instance, Montana and Davis [1989] utilized a GA instead of a standard training algorithm such as back-propagation to find a good set of weights for a given architecture. It is reasoned that the advantage of using GA's instead of back-propagation lies in the latter's tendency to get stuck at local optima, or the unavailability of a large enough set of training patterns for certain tasks [Mitchell, 1996a]. I explore the problem here, not to prove or disprove its merits, but simply because it is usually a very computationally demanding problem, which can potentially benefit from the chromosomal information compression offered by CGA's with fuzzy indirect encoding.

The set of weights of a neural network defines a vector of real values. Montana and Davis' network required a vector of 126 weights to evolve. Because the weights are real-valued, they used what is usually referred to as the real encoding of chromosomes in a GA. That is, instead a binary strings as chromosomes, a real-encoded GA uses strings of real numbers. The operation of mutation is now different: a random number is added to each element of the vector with low probability. Montana and Davis also used a different kind of crossover operation, the details of which are unnecessary for the current presentation (see Montana and Davis [1989] for more details).

2.2.1 Hand-Written Character Recognition: The Network Architecture

I applied the CGA with fuzzy indirect encoding to a problem that requires larger real-valued chromosome vectors. The problem I approached was that of the recognition of hand-written characters in an 8 by 10 grid⁽³⁸⁾: each pattern is defined by an 80 bits long vector. There were a total of 260 patterns available, which contained 5 different categories, that is 5 different hand-written characters with 52 instance patterns each. The patterns were divided equally between the learning and the validation sets, preserving the ratios per category. In other words, the learning and the validation sets contained both 130 patterns, 26 patterns for each of the 5 categories.

Since each pattern is an 80-length bit vector, the input layer to the neural network has also 80 nodes, plus one for the bias unit. The output layer requires only 3 nodes, whose binary output encode 5 categories (3 nodes can encode up to 8 categories). Experiments were ran with a hidden layer of 2 and 5 Nodes. The information requirements of the sets of weights for these architectures are summarized in the following table:

Neural Network Architecture with 81 input nodes and 3 output nodes
Hidden Nodes	2	5
Number of Weights	171	423
Bits of Information (4 byte real number)	5472	13536

Thus, the real encoded GA requires chromosomes defined by real-valued vectors of length 171 and 423, for the 2 and 5 hidden nodes architectures, respectively. Such vectors actually cost some computer implementation 5472 and 13536 bits of information each (assuming an implementation where real numbers are only 4 bytes long which is actually rather small).

2.2.2 Results from Back-Propagation

This section is not included, please refer to the postscript version

2.2.3 Results from Real-encoded GA

This section is not included, please refer to the postscript version

2.2.4 Results from CGA with Fuzzy Indirect Encoding

This section is not included, please refer to the postscript version

2.3 Discrete Variables: Evolution of Cellular Automata Rules

This section is not included, please refer to the postscript version

2.4 The Effectiveness of Computational Embodiment: Epistasis and Development

The introduction of an intermediate development layer in CGA's serves to reduce the size of genetic descriptions (see chapter 4). This is done because some fixed computationally building blocks are assumed for any problem we encode. Chromosomes code for these building blocks which will themselves self-organize (develop) into a final configuration. The algorithm used in this chapter achieves precisely that. It is an instance of the selected self-organization ideas presented in chapter 2. The developmental stage is in effect simulating some specific dynamic constraints on evolution posed by a simulated embodiment of the evolving semiotic system.

Fuzzy indirect encoding captures computationally the advantages of materiality by reducing genetic descriptions, which may be very relevant in practical domains such as data mining. However, it does also capture the reverse side of embodiment, that is the limiting constraints that a given materiality poses on evolving systems. Given a specific simulated embodiment defined by the particular fuzzy set shapes and operations used (see section 2.1), the algorithm cannot reach all portions of space of solutions. It can only reach those solutions that can be constructed from the manipulation of the allowed fuzzy sets and operations - the building blocks. This echoes my early observation (see chapter 2 and 4), that the genetic system is similarly not able to evolve anything whatsoever, but only forms that can be built out of aminoacid chains. Such constraints are observed on the problems of sections 2.2 and 2.3, as the solution vectors obtained by the indirect encoding scheme are much less random than the solutions obtained by direct encoding. The solutions reached are much more ordered, in other words, the inclusion of the developmental stage introduced a lot of order "for free". Such order was not a result of the selection mechanism, but of the intrinsic dynamics the system possesses (the developmental rules) that tends to produce mostly ordered solutions.

Another way to think of this, is that in traditional GA's, each position of the solution vector maps to only one position in the chromosomes (allele), which can be independently mutated. In other words, the mutation of one bit in the chromosome will affect only one component in the solution vector. Whereas in the indirect encoding scheme, each bit of the chromosomes affects several elements of the solution vector non-linearly. In the scheme here utilized, flipping one bit in the FDP may result in changing a fuzzy set operation to another, thus causing the fuzzy sets it operates on to be connected in a totally different manner for all its elements. Thus, one single bit of indirectly encoded chromosomes can affect many, potentially all, elements of the solution vector as the development program is changed. This introduces epistasis to evolutionary computation, which we know exists in natural genetic systems.

All of these aspects of indirectly encoded GA's, both enabling constraints such as genetic information compression, and limiting constraints such as reduction of the space of solutions, are desired of models of evolutionary systems. But what does it mean for practical applications in data mining? Genetic compression is obviously a plus, but the limiting constraints may be problematic if the reduced search space includes only mediocre solutions to our problems. When genetic descriptions are not very large, the only reason to use indirect encoding is if we wish to avoid very random solution vectors that tend to be produced with GA's. This was the case of the evolution of neural network weights in section 2.2. The indirect encoding scheme was able to produce better cross-validation results. Due to its intrinsic order, its solutions did not overly adapt to the patterns in the learning set. When the genetic descriptions are very large, or require real-encoding (such as the case of section 2.2), then it is advantageous to use indirect encoding. Sometimes, even if the reduced solution space is mediocre, such less that optimum solutions might be all that we can hope to find in huge solution spaces, inaccessible to standard GA's due to computational limitations.

CHAPTER 6

SIMULATIONS OF EMBODIED EVOLVING SEMIOSIS

It is one simple idea that unites the present work: Embodied Evolving Semiosis (EES). It takes the form of Selected Self-Organization in the study of biological systems, and Evolutionary Constructivism in the study of Cognitive Systems. EES defines an inclusive position between that bridges the self-organizing with the symbolic paradigm. It asserts that the modeling of living phenomena cannot do without some account of both self-organization and symbolic representation (genetic or cognitive). EES understands the living organization to be comprised of self-organizing principles, which in (situated) interaction with an environment define inert (stable) memory structures that can be used to classify such interaction (see chapter 2). The particular material, situated interaction with an environment defines the universe of possible inert structures which determines the universe of constructed classification. In other words, the living organization requires embodied semiosis with an environment which in turn requires the notion of semantic emergence in addition to mere self-organizing emergence as discussed in chapter 2.

If the inert structures have more explicit symbolic attributes beyond dynamic classification, then the evolutionary potential of embodied semiosis becomes open-ended (see chapter 2). That is, if the classification of the situated interaction between living system and environment is based on local and not distributed memory, and is tied to a selection mechanism, we reach EES. In biological systems this is achieved with the description-based self-reproducing scheme of Von Neumann which effectively describes genetic-based natural selection. In cognitive systems, linguistic categorization may offer a similar selection mechanism which is based on social consensus.

In summary, EES requires:

Material self-organization in situated interaction with an environment
Semantic emergence: classification based on structural perturbation of self-organizing dynamics by inert memory structures that define a material symbol system
Selection in an environment leading to open-ended evolution

The first point implies the notion of embodiment. 1 and 2 imply the notion of emergent classification (semantics), that is, classifications are relative to the situated interaction of a living system with its environment and its ability to construct internal stabilities. Point 2 refers to the establishment of a descriptional syntax necessary to achieve open-endedness. Point 3 effectively grounds the personal, situated construction of points 1 and 2 in a particular environment which is common to other living systems. It is therefore a pragmatic dimension that leads living systems' classifications to be coherent with their environments in order to survive or effectively communicate. Genetic based natural selection evolves organisms that can coherently classify their environments well enough to persist. Linguistic interaction establishes a consensual selection of the personal constructions of cognitive systems so that they can coherently interact with one another. Points 1, 2 and 3 establish a complex system's semiosis with its environment by defining a pragmatic semantics of situated interaction. Syntax is defined by the mechanisms that manipulate the necessary internal inert structures.

Though allowing for open-ended evolution (as described in chapter 2), material symbol systems are nonetheless constrained in what they can describe. This point refers to the parts problem as stated by Von Neumann, and it was computationally modeled with the Contextual Genetic Algorithms experiments of chapter 5. This point was defended only for biological systems, since we have no evidence of the mechanisms that actually implement a system of linguistic structural perturbation in cognitive systems which can "rewire" cognitive emergent classification. In biological systems we have recognized the genetic system as the mechanism of structural perturbation which allows us to discuss its limitations in terms of the Parts Problem. Until more knowledge is gained about language and the brain the argument for EES in cognitive systems is more restricted than the one for biological systems (more on this in the next section). Notice that the application Talkmine developed in chapter 5 as a model of cognitive categorization, does establish an adaptive mechanism to "rewire" its long-term associative structure as it is perturbed by a system of linguistic interaction with its users based on short-term categorization. What was not studied were the limitations of such a "rewiring" mechanism. Figures 1 and 2 depict the skeleton of the arguments developed in this dissertation for selected self-organization and evolutionary constructivism respectively.

1. What Would Invalidate EES?

For EES to be wrong, one of the three points discussed above would need to be proved false. Ample evidence has been given for the self-organizing characteristics of living systems in interaction with an environment [e.g. Kauffman, 1993; Goodwin, 1994; Salthe, 1995] in what is often referred to as the structuralist position. Much evidence has also been compiled for the self-organizing characteristics of cognitive systems [e.g. Churchland and Sejnowski, 1991; Varela, Thompson, and Rosch, 1991; Clark, 1993] in connectionist cognitive science.

That natural selection occurs in living systems is rarely disputed even by the most ardent structuralists. What may be debated is the extent of its influence. This is largely irrelevant for EES as it implies a case by case credit assessment of different aspects of living systems (see chapter 2). Much evidence has also been given for the mechanisms of social consensual selection of cognitive classifications (cognitive development) in education theory and psychology [e.g. Piaget, 1971; Pask, 1975; von Glasersfeld, 1993].

The second point may require more caution. It is the existence of material inert memory structures functioning as symbols that are used in the classification of an environment, as well as in establishing a relation to dynamic building blocks that eventually construct a self-organizing classification. If no such inert structures are proved to exist in biological and cognitive systems, then EES as described in the present work is not a valid systems theoretic framework to study the living organization, biological or cognitive.

In biological systems, the existence of these inert structures is well established. Indeed, the genetic system defines an effectively symbolic coded relation between genes and aminoacid chains that develop into phenotypes. Genes, though probably more dynamic than usually thought of, are based on DNA molecules which naturally have some dynamic properties. However, when used as descriptions of aminoacid chains DNA molecules are essentially inert information carriers, since their function in the genetic system is not defined by their minimal reactive chemical characteristics but by the sequence of constituents (nucleotides) they are comprised of. Changing this sequence does not change the reactive, dynamic, characteristics of the DNA molecule, but it changes the information it carries to the genetic decoding machinery. It is also understood that genes act as the vehicles of descriptional variation necessary to define von Neumann's scheme of open-ended evolution. Therefore, for biological systems EES has been all but proved, even though the advantages of using such complete semiosis in living organisms are usually not fully understood. The Contextual Genetic Algorithms presented in chapter 4 and 5 aim precisely at the exploration of these advantages whose results are discussed in the next section.

In cognitive systems the story is quite different since no such inert structures have been found. I am convinced that some form of such structures will one day be discovered, but if the reverse is eventually proved, that is, that no such structures exist, then EES will not be valid for cognitive systems. We have plenty of evidence for the self-organizing, connectionist, attributes of cognition, which is effectively non-symbolic [Varela, Thompson, and Rosch, 1991]. However, all current models of connectionism are very incomplete at describing cognitive behavior, in particular its metaphoric characteristics and open-ended associative power. This leads some [e.g. Clark, 1993] to defend that connectionism is only part of the story, and that cognition cannot be completely characterized by non-representational, action-reaction, self-organizing situated interaction. Since connectionist models cannot efficiently deal with open-ended contextual dependencies and metaphor, all bets are still open as to what constitutes the nature of cognitive behavior, at least until we learn more about the brain.

In Chapter 3 and 5 I developed a model of cognitive categorization using evidence sets, which culminated in the TalkMine application. This model proposes that prototype linguistic categories function as a temporary system of structural perturbation of an array of context-specific dynamic networks that keep long-term associations in a connectionist manner. The consensual selection of these categories by the environment eventually adapts the long-term associations to such environment. It is a representational mechanism of structural perturbation and, given a large number of context-specific networks, offers the ability of open-ended, multi-context, categorical constructions. The long-term connectionist networks can be seen as the dynamic building blocks necessary for environmental classification, while the short-term categories offer the ability to harness such dynamics, with a specific syntax defined in TalkMine by Evidence Sets. Furthermore, these categories offer a selection mechanism in consensual environmental interaction through conversation with other categorizing systems. If such a system of structural perturbation does occur in the brain, then some sort of information carrier for these short-term categories will have to be found.

2. What Does EES Have to Offer to AI and AL?

Besides identifying the concept of EES in its varieties of Selected Self-Organization and Evolutionary Constructivism as a systems theoretic framework for biological and cognitive systems, the purpose of this dissertation is to actually propose models for AI and AL that take advantage of the EES concept. Figure 3 shows the layout of the dissertation in trying to achieve this. In chapter 2 EES was explored philosophically, while chapters 3 and 4 approached the subject from the point of view of cognitive and biological systems respectively. Chapter 5 described the computational applications that can be built from the EES framework with significant practical application potential.

2.1 Evolutionary Constructivism and AI

Evidence Sets were proposed as models of short-term prototype categories in an Evolutionary Constructivist framework that assumes a connectionist, self-organizing, long-term memory organization. Evidence Sets model the subjective, context-dependent, uncertain, linguistic categories that are to be used in a socially consensual system of structural perturbation of long-term networked memory. These ideas are then implemented in the TalkMine application of Chapter 5. TalkMine does not use distributed connectionist networks for its long-term memory banks but a relational database structure which captures many of the desired characteristics of connectionist machines (see chapters 3 and 5). In this sense, it offers a hybrid architecture which simulates both the personal, self-organizing, construction of long-term associations and the communicatable, short-term, categories that allow the system to adapt to its environment as it interacts with its users. This defines the desired Selected Self-Organization or Evolutionary Constructivism in a computational environment.

Furthermore, it is by virtue of this system of short-term construction of categories which perturbs the long-term networked memory banks, that the bringing together of many different contexts is attained. The possibility of utilization of many contexts establishes a virtually open-ended association mechanism capable of relating concepts that would otherwise be highly distinct. Such capability effectively simulates metaphorical categorizations (see chapter 5). The continued development of systems such as TalkMine and Evidence Sets, is necessary in order to lead AI away from fruitless debates over the merits of self-organizing or symbolic paradigms. If we accept cognition to depend on EES, then the future of AI should be on hybrid structures such as TalkMine that try to bridge the gap between self-organizing constraints and symbolic open-endedness, and in so doing define very useful applications for data-mining problems.

2.2 Selected Self-Organization and AL

Similarly Contextual Genetic Algorithms (CGA's) were proposed as means to model more accurately the self-organizing, developmental, constraints of genetic driven Natural Selection in a Selected Self-Organization framework. The inclusion of indirect encoding between genetic descriptions and problem solutions in evolutionary computation applications, is an attempt to simulate embodiment in a computational realm. The results obtained with the Fuzzy Development Programs (FDP) CGA's in chapter 5, which allow large information reduction of genetic descriptions, show the advantages of applying the EES concept to evolutionary computation. They also show that the evolution of solutions for a given problem depends on the particular (simulation of) dynamic building blocks of the genetic system. In the FDP CGA's, this means that the pool of Fuzzy Set shapes and operations selected dictates the space of solutions that be constructed. In other words, Fuzzy Sets work as the material building blocks that constrain the evolutionary potential of an (artificially) embodied symbol system.

The CGA model implements both enabling and restraining constraints of evolutionary systems. The existence of a finite number of building block eases the information necessities of genetic descriptions, enabling the construction of complex solutions from simple descriptions. On the other hand, depending on the richness of these building blocks, the space of possible solutions is restrained since not all possible solutions can be reached, but only those that can be built out of these building blocks. If the EES framework is right, that is if evolutionary systems are based on embodied evolving symbol systems, that follow Von Neumann's scheme of descriptional selection but which equally emphasize the dynamic constraints of a symbol system's building blocks (the parts problem), then AL must be preoccupied with models of life-as-it-could-be that explicitly define a particular simulated embodiment from which the living organization is constructed.

The CGA model of chapter 5 shows that genetic driven selection leads evolving symbol systems to seek higher values of fitness only in so far as its specific embodiment can reach them. Evolution is open-ended only in the context of a given set of material building blocks. Thus, AL, like AI, should avoid the fruitless debate over the supremacy of selection or structure, and devote itself to inclusive strategies that incorporate notions from both paradigms. AL can indeed offer the right forum to implement a new synthesis of these two camps of evolutionary thought, by investigating computationally the relative importance of the several factors that define evolutionary systems. In other words, AL is the ideal field to study the credit assignment problem of evolutionary systems. The CGA model developed in chapters 4 and 5 offers the possibility of studying how the same problem (same fitness) can be solved by differently embodied, evolving, symbol systems defined by different sets of Fuzzy Set building blocks. In this sense, the CGA model opens the door to an inclusive, synthetic, theory of Artificial Evolutionary Systems.

3. Limitations of EES

3.1 The Origin Problem

EES as presented in the present work does not address the origin of semiosis itself. It defends that the living organization requires symbolic representation to be accurately simulated, but the arguments on which it is based follow from ample evidence obtained from the observation of biological and cognitive systems - the genetic and natural language systems. The problem of the origin of symbolic representation is not discussed. How is it that symbols appear in the living organization from a non-informational milieu is a question that is beyond the scope of this work. Indeed, such is the main question that any theory of the origin of life or cognition must answer. EES can only stress the central importance of the concept of embodied semiosis. It may therefore offer yet another modest push to direct the research of problems of origin to the mechanisms that would allow the emergence of semiosis from self-organization.

3.2 Computational Limitations

The computational models of EES developed in chapter 5 one way or another struggle with the necessity of simulating a dynamic self-organizing system which is harnessed or structurally perturbed by some representational syntactic manipulations. TalkMine uses the language of Evidence Sets to structurally perturb a model of dynamic representation defined by relational databases, leading the associative memory banks to match the expectations of the consensus of its users. The CGA model uses a genetic variation engine to perturb a dynamic system simulated by Fuzzy Sets which can construct solutions for some problem.

The problem of building models of EES such as TalkMine and CGA's in an universal computation environment is that, at some level of the simulation, the dynamics of self-organization must also be symbolically computed. In natural EES systems, matter does not have to compute its next state as it self-organizes, but merely follow the laws of physics. When we use universal computers, every single aspect of the simulation must be computed. For instance, natural genetic systems do not have to describe the phenotypes they produce in all their physical details, instead they merely have to describe the set of aminoacid chains that develops into such phenotypes. In other words, the natural embodied semiosis of biological systems utilizes pre-existing order that "comes for free" with the laws of matter. Conversely, computational simulations of these systems must not only describe the genetic descriptions but also the self-organizing dynamics in all of its details, which burdens simulations tremendously.

The models developed in chapter 5 try to simplify the simulation of dynamic interactions as much as possible and still preserve some of the essential characteristics of self-organizing, connectionist, dynamics. TalkMine uses relational databases instead of true connectionist machines precisely to avoid the lengthy process of re-training that such systems require, which is nothing more than the simulation of self-organizing classification behavior. This move allows TalkMine to maintain the required associative metric produced by connectionist machines with a simpler re-computation algorithm (see chapters 3 and 5). The FDP CGA uses a Fuzzy Set system of representing a dynamical system without actually implementing one also to avoid lengthy computations. FDP's maintain some characteristics of dynamic development (see chapter 4) but are not truly dynamic. In this sense, both TalkMine and the FDP CGA's try to streamline as much as possible the computational requirements of EES in a universal computer environment.

In order to build better models of EES we would do well by abandoning the universal computer framework and utilize genuinely hybrid computation environments. In other words, instead of using universal computers we might use problem-specific computers, also known as analogues. Consider the FDP CGA model. If the FDP's instead of being implemented in a program for a universal computer, were actual physical building blocks observing the desired behavior, then the software part would only have to implement the genetic variation engine which would harness such physical building blocks that do not require simulation. If the analogue part is fast enough, then we would save tremendously on computer resources and computation time.

Universal computation environments are based on a hierarchy of virtual machines that eventually produces a sequence of binary operations implemented in silicon flip-flops. As this hierarchy becomes more and more sophisticated, say with the development of visual object oriented programming, the size of the lower level binary operations needs to increase dramatically. By using problem-specific analogues, we can do without this complicated hierarchy at least when it comes to constant aspects of our computations. Universal computation by definition is designed to as independent as possible of physical law, while requiring the highest amount of syntactic description. Problem-specific analogue computation, harnesses more complicated physical processes that spontaneously follow pre-defined, unprogrammed, dynamic behavior thus requiring much smaller descriptions, though, of course, reducing the scope of possible problems that can be computed. In order to simulate complex systems that observe EES we would be better off with such hybrid computational/analogue systems precisely because EES demands the simulation of self-organizing dynamics that analogues could offer without computational expenses. Perhaps in the future, research into molecular computation might establish such a framework.

In the meantime, the FDP CGA model can be made much more effective if the Fuzzy Set building blocks are hardwired into a separate silicon chip that the universal computer can access without simulating it. Once a good pool of Fuzzy Set shapes and operations is found for a set of problems, they can be hardwired so that the software variation engine can act on them to construct solutions in a much faster way. In other words, if the indirect encoding layer of CGA's is substituted by a very fast physical process with some fixed, known characteristics, then the genetic variation engine would only trigger a true material development layer which would be in turn interpretable as a solution. This would establish a hybrid software/hardware system for optimization of informationally expensive problems.

Hence, in order to pursue richer models of EES, we need to do more than just simulating materiality, but actually use it. Practically, this means leading AI and AL more and more into the area of situated robotics and cognition. This direction of research re-emphasizes the earlier cybernetic vision of hybrid machines that intertwine computation and true self-organization in order to simulate the living organization in embodied interaction with an environment. Pragmatically it requires the investigation of good material substrates that can establish true, fast, self-organizing behavior in order to bypass lengthy hierarchical universal computation that must eventually boil down to the "chunk-chunk-chunk" of silicon 0's and 1's. Being an inclusive idea, EES does not imply the abandonment of symbolic computation, not at all, but it does alert us to a theory of life and cognition that must pragmatically use both universal computation and analogue self-organization in its models as previously defended by Cariani[1989].

4. Future Directions and Conclusions

Several formalisms and models were proposed in this dissertation to establish EES as a systems-theoretic framework for biological and cognitive systems. Even though good computational results were obtained from these models, there is ample room to develop them into richer formalisms.

Many avenues exist to develop and affirm evidence sets as robust mathematical structures to model linguistic uncertainty, a list of a few of these is presented next:

The study of information measures developed in section 5 of chapter 3 can address the very recent developments in the measurement of nonspecificity in nonsdiscrete domains, by discussing Klir and Yuan's [1995] Hartley-like measure in terms of the general measure of nonspecificity (11) proposed in section 5 of chapter 3. The computational simplicity of the relative measures of uncertainty developed in section 5.4 of chapter 3 can be evaluated by comparing them to standard measures of uncertainty.
A more complete belief-constrained theory of approximate reasoning can be pursued by proposing more operators for evidence sets such intersections and unions with extended range of operations. The combination of the belief qualification of evidence sets can be studied in more detail in order to develop more sophisticated forms of context preservation in linguistic categories.

Evidence sets can be compared to additional models of uncertain linguistic categories and belief formalisms such as the possible-world semantics of modal-logics, fuzzy rough sets, rough fuzzy sets, etc. This study should pay attention to the computational costs of the different approaches as computational models of linguistic categories.
The definition of -cuts for Evidence Sets can be pursued.

Similarly, contextual genetic algorithms can be better established as valid tools for evolutionary computation by pursuing different avenues:

More experiments should be made with different classes of computationally demanding problems. Only the repeated success of the scheme when applied to different classes of problems can establish it as a valid evolutionary computation tool.
Good pools of fuzzy set operations and shapes for different classes of problems can be investigated. Heuristics should be developed to aid the selection of such pools for particular problems.
Once good pools are discovered, they can be hardwired to obtain much faster evolution of solutions for general classes of problems. The software part of the implementation would be responsible for the genetic variation and decoding portions of the algorithm, while the hardwired part would be responsible for the development portions.
Artificial life models of environmental influence in genetic transcription and phenotypic development can be implemented and evaluated.
Artificial Life models of hierarchical development can be pursued. In this case, the building blocks that build the solutions (the fuzzy sets) should have several stages of development.

I consider the research presented in this dissertation to be an exploration into the coupling of symbolic controls to self-organizing dynamics. Computational models were developed in order to explore the limits of current universal computation techniques as models of EES. Many practical applications spin off this dissertation, which emphasize both the power and limits of symbol manipulation coupled to self-organization. Evidence Sets enlarged the mathematical study of linguistic uncertainty as an extension of Zadeh's Fuzzy Sets by explicitly formalizing subjective context-dependencies. When coupled to networked memory structures, they also offer a model of cognitive categorization, which is used in the development of the useful database retrieval system TalkMine. Contextual Genetic Algorithms enlarge evolutionary computation as proposed by Holland, by including non-linear, self-organizing, relations between genetic descriptions and solutions to optimization problems. The FDP CGA experiments of chapter 5 demonstrate the power of this expansion. The underlying conclusion to the present work is that both symbols and dynamics are important to models of evolving cognitive and biological systems, and that the key to these complex systems is precisely the integration of both of these aspects.

REFERENCES

Arbib, M.A. [1966]."A simple self-reproducing universal automaton." Information and Control. Vol. 9, pp. 177-189.

Arbib, M.A. [1967]."Automata theory and development: Part I." Theoretical Biology. Vol. 14, pp. 131-156.

Arbib, M.A. [1987]. Brains, Machines, and Mathematics. (2nd Edition). Springer-Verlag.

Aronson, J.L., R. Harré, and E.C. Way [1995]. Realism Rescued: How Scientific Progress is Possible. Open Court.

Ashby, W.R. [1962]."Principles of the self-organizing system." In: Principles of Self-Organization. H. von Foerster and G.W. Zopf (eds.). Pergamon Press. Reprinted in Klir [1991], pp. 521-536.

Atanassov, K. [1986]."Intuitionistic fuzzy sets." fuzzy Sets and Systems . Vol. 64, pp. 159-174.

Atanassov, K. [1994]."Operators over interval valued intuitionistic fuzzy sets." Fuzzy Sets and Systems. Vol. 64, pp. 159-174.

Atanassov, K. and G. Gargov [1994]."Interval valued intuitionistic fuzzy sets." Fuzzy Sets and Systems. Vol. 31, pp. 343-349.

Barsalou, L. [1987]."The instability of graded structure: implications for the nature of concepts." In: Concepts and Conceptual Development: Ecological and Intellectual Factors in Categorization. U. Neisser (ed.). Cambridge University Press.

Benne, R. (Ed.) [1993]. RNA Editing: The Alteration of Protein Coding Sequences of RNA. Ellis Horwood Publishers.

Benne, R., J. van den Burg, J.P.J. Brakenhoff, J.H. van Boom, and M.C. Tromp [1986]."Major transcript of the frameshifted coxII gene from trypanosome mitochondria contains four nucleotides that are not encoded in the DNA." Cell. Vol. 46, pp. 819-826.

Bickerton, D. [1990]. Language and Species. University of Chicago Press.

Bickhard, M.H. and D.M. Richie [1983] On the Nature of Representation. Praeger.

Blum, B., N. Bakalara, and L. Simpson [1990]."A model of RNA editing in kinetoplast mitochondria: "guide" RNA molecules transcribed from minicircle DNA provide the edited information." Cell. Vol. 60, pp.189-198.

Boulding, K. E. [1956]."General Systems Theory - the skeleton of science." Management Science. Vol. 2, pp. 197-208. Reprinted in Klir [1991] pp. 239-248.

Brooks, R.A. [1991]."Intelligence without reason." In: Proceedings of the 12th International Conference on Artificial Intelligence, San Mateo 2992. . Morgan Kaufmann.

Buss, L. [1987]. Evolution of Individuality. Princeton University Press.

Campbell, D.T. [1974]."Evolutionary Epistemology." In: The Philosophy of Karl Popper. P.A. Schilpp (ed.). Open Court Publishers, pp. 413-463.

Cariani, Peter [1989]. On The Design of Devoces With Emergent Semantic Functions. PhD Dissertation. State University of New York at Binghamton.

Cariani, Peter [1992]."Emergence and Artificial Life." In: Artificial Life II. C. Langton, C. Taylor, J.D. Farmer, and S. Rasmussen (eds.). SFI Series in the Sciences of Complexity. Addison-Wesley, pp. 775-797.

Cariani, Peter [1995]."Towards an evolutionary semiotics: the role of symbols in organisms and adaptive devices." In: International Seminar on Evolving Systems, Vienna, 1995. G. Van de Vijver and S. Salthe (eds.). Kluwer (In Press).

Cassirer, E. [1946]. Language and Myth. Dover.

Chomsky, N. [1965]. Aspects of the Theory of Syntax. MIT Press.

Churchland, P. and T. Sejnowski [1992]. The Computational Brain. MIT Press.

Clark, Andy [1993]. Associative Engines: Connectionism, Concepts, and Representational Change. MIT Press.

Clark, Andy [1996]."Happy couplings: emergence and explanatory interlock." In: The Philosophy of Artificial Life. M. Boden (ed.). Oxford University Press, pp. 262-281.

Conrad, Michael [1983]. Adaptability. Plenum Press.

Conrad, Michael [1990]."The geometry of evolutions." BioSystems. Vol. 24, pp.61-81.

Crutchfield, J.P. and M. Mitchell [1995]."The evolution of emergent computation." Proc. National Academy of Sciences, USA, Computer Sciences. Vol. 92, pp. 10742-10746.

Dawkins, R. [1976]. The Selfish Gene. Oxford University Press.

Dawkins, R. [1987]. The Blind Watchmaker: Why the Evidence of Evolution Reveals a Universe Without Design. Norton.

de Cooman, G., D. Ruan, and E. Kerre (eds.) [1995]. Foundations and Applications of Possibility Theory. World Scientific.

Dellaert, Frank and R.D. Beer [1994]."Toward an evolvable model of development for autonomous agent synthesis." Artificial Life IV. R. Brooks and P. Maes (eds.). MIT Press. pp. 246-257.

Dempster, A. [1967]."Upper and lower probabilities induced by multivalued mappings." Annals of Mathematical Statistics. Vol. 38, pp. 325-339.

Dennet, D.C. [1995]. Darwin's Dangerous Idea: Evolution and The Meanings of Life. Simon and Schuster.

Derrida, J. [1988]. Limited Inc. Northwestern University Press.

Dinsmore, J. (ed.) [1992]. The Symbolic and Connectionist Paradigms: Closing the Gap. Lawrence Erlbaum.

Dubois, D. and H. Prade [1985]."A note on measures of specificity for fuzzy sets." International Journal of General Systems. Vol. 10, pp. 279-283.

Dubois, D. and H. Prade [1986]."A set-theoretic view of belief functions: logical operations and approximations by fuzzy sets." Int. Journal of General Systems. Vol. 12, pp. 193-226.

Dubois, D. and H. Prade [1987]."Properties of measures of information in evidence and possibility theories." Fuzzy Sets and Systems. Vol. 24, pp. 161-182.

Eigen, M. [1992]. Steps Towards Life: A Perspective on Evolution. Oxford University Press.

Eldridge, N. [1995]."A battle of words." In: The Third Culture: Beyond The Scientific Revolution. J. Brockman. Simon and Schuster, pp.119-128.

Etxeberria, Arantza [1995]."Embodiment of Natural and Artificial Agents." In: International Seminar on Evolving Systems, Vienna 1995. G. van de Vijver and S. Salthe. Kluwer.

Fillmore, C. [1982]."Frame semantics." In: Linguistics in the Morning Calm. Linguistics Society of Korea. Hanshin, pp. 111-138.

Fodor, J. [1981]. Representations: Philosophical Essays on the Foundations of Cognitive Science. MIT Press.

Forrest, S. (ed.) [1991]. Emergent Computation. MIT Press.

Galvin, F. and S.D. Shore [1991]."Distance functions and topologies." The American Mathematical Monthly. Vol. 98, No. 7, pp. 620-623.

Glanville, R. [1988]. Objekte. Merve Verlag.

Glanville, R. [1994]."as if." In: Cybernetics and Systems 94. R. Trappl (ed.). Vol.1, pp. 613-620.

Goldberg, D.E. [1989]. Genetic Algorithms in Search, Optimization, and Machine Learning. Addison-Wesley.

Goodwin, B. [1994]. How the Leopard Changed its Spots: The Evolution of Complexity. Charles Scribner's Sons.

Gorzaczany, M.B. [1987]."A method of inference in approximate reasoning based on interval-valued fuzzy sets." Fuzzy Sets and Systems. Vol. 21, pp. 1-17.

Gould, S.J. [1989]. Wonderful Life. Norton.

Gould, S.J. [1995]."The pattern of life's history." In: The Third Culture: Beyond the Industrial Revolution. J. Brockman (ed.). Simon and Schuster, pp. 51-73.

Gruau, F. [1992]."genetic synthesis of boolean neural networks with a cell rewriting developmental process." In: Proceedings of the International Workshop on Combinations of Genetic Algorithms and Neural Networks. L.D. Whitley and J.D. Schaffer. IEEE Press, pp. 55-74.

Haken, H. [1977]. Synergetics. Springer-Verlag.

Hamming, R.W. [1980]. Coding and Information Theory. Prentice-Hall.

Hampton, J. [1992]."Prototype models of concept representation." In: Categories and Concepts: Theoretical Views and Inductive Data Analysis. I. Van Mechelen, J.Hampton, R. Michalski, and P.Theuns. Academic Press.

Harmanec, D. and G. Klir [1994]."Measuring total uncertainty in Dempster-Shafer theory: a novel approach." Int. J. of General Systems. Vol. 22, pp. 405-419.

Hartley, R. [1928]."Transmission of informations." In: The Bell System Technical Journal. Vol. 7, pp. 31-46.

Henry, C. and L.M. Rocha [1996]."Language theory: consensual selection of dynamics." In: Cybernetics and Systems: An International Journal. . Vol. 27, pp 541-553.

Henry, Charles [1995]."Universal Grammar." Communication and Cognition - Artificial Intelligence. Vol. 12, Nos. 1-2, pp. 45-62.

Heylighen, F. and C. Joslyn [1992]."Physical constructivism." Principia Cybernetica Web. WWW document: http://pespmc1.vub.ac.be/physcons.html.

Higashi, M. and G. Klir [1983]."Measures of uncertainty and information based on possibility distributions." Int. J. of General Systems. Vol. 9, pp. 43-58.

Hirota, K. [1981]."Concepts of probabilistic sets." Fuzzy Sets and Systems. Vol. 5, pp. 31-46.

Holland, J.H. [1975]. Adaptation in Natural and Artificial Systems. University of Michigan Press.

Holyoak, K.J. and P. Thagard [1995]. Mental Leaps: Analogy in Creative Thought. MIT Press.

Hooker, C.A. [1995]. Reason, Regulation and Realism: Towards a Regulatory Systems Theory of Reason and Evolutionary Epistemology. State University of New York Press.

Hordijk, W., J.P. Crutchfield, and M. Mitchell [1996]."Embedded-particle computation in evolved cellular automata." In: Proceedings of Physics and Computation 96. In Press. Available as a Santa Fe Institute preprint (96-09-073).

Husbands, P., I. Harvey, D. Cliff, and G. Miller [1994]."The use of genetic algorithms for the development of sensorimotor control systems." In: Proc. of the International Workshop from Perception to Action. P. Gaussier and J. Nicoud (eds.). IEEE Press, pp. 110-121.

Jacobson, P. [1982]. The Nature of Syntactic Representation. Kluwer.

James, W. [1892]. Psychology: The Briefer Course. University of Notre-Dame Press, 1985..

Kampis, George [1991]. Self-Modifying Systems in Biology and Cognitive Science. Pergamon Press.

Kauffman, S. [1993]. The Origins of Order: Self-Organization and Selection in Evolution. Oxford university Press.

Kauffman, S. [1995]."Order for free." In: The Third Culture: Beyond the Scientific Revolution. J. Brockman (ed.). Simon and Schuster, pp. 333-343.

Kitano, H. [1994]."Evolution of metabolism for morphogenesis." In: Artificial Life IV. R.A. Brooks and P. Maes (eds.). MIT Press. pp 49-58.

Kitano, H. [1995]."Cell differentiation and neurogenesis in evolutionary large scale chaos." In: Advances in Artificial Life. F. Moran et al (Eds.). Springer-Verlag. pp. 341-352..

Klir, G.J. and T. Folger [1988]. Fuzzy Sets, Uncertainty, and Information. Prentice Hall.

Klir, G.J. and B. Parviz [1992]."A note on the measure of discord." In: Proceedings of the Eigth Conference on Artificial Intelligence. D. Dubois (ed.). Morgan Kaufmann, pp. 138-141.

Klir, G.J. and A. Ramer [1990]."Uncertainty in the Demster-Shafer theory: a critical re-examination." Int. J. of General Systems. Vol. 18, pp. 155-166.

Klir, G.J. and M.J. Wierman [1997]. Uncertainty-Based Information: Elements of Generalized Information Theory. Lecture Notes in Fuzzy Mathematics and Computer Science. Creighton University, Omaha, Nebraska.

Klir, G.J. and B. Yuan [1993]."On measures of conflict among set-valued statements." In: Proceedings of the 1993 World Congress on Neural Networks; July 11-15, 1993, Portland. Oregon. pp. 627-630.

Klir, G.J. and B. Yuan [1995]. Fuzzy Sets and Fuzzy Logic: Theory and Applications. Prentice Hall.

Klir, George, J. [1991]. Facets of Systems Science. Plenum Press.

Klir, George, J. [1993]."Developments in uncertainty-based information." In: Advances in Computers. M. Yovits (Ed.). Vol. 36, pp. 255-332.

Kramosil, I. [1995]."Believeability and plausibility functions over infinite sets." Int. J. of General Systems. Vol. 23, pp. 173-198.

Lakoff, G. [1987]. Women, Fire, and Dangerous Things: What Categories Reveal about the Mind. University of Chicago Press.

Langton, C.G. [1989]."Artificial life." In: Artificial Life. C. Langton (ed.). Addison-Wesley.

Langton, C.G. [1990]."Computation at the edge of chaos: phase transitions and emergent computation." Physica D. Vol. 42, pp. 12-37.

Laszlo, E. [1987]. Evolution: The Grand Synthesis. New Science Library.

Leduc, S. [1911]. The Mechanism of Life. Renman, London..

Lee, K.M., J. Favrel, H. Lee-Kwang, and C.B. Kim [1996]."Fuzzy convolution as a nonlinear digital filter." In: Proceedings of the 1996 NAFIPS Conference, Berkley 1996. M.H. Smith, M.A. Lee, J. Keller, and J. Yen (eds). IEEE Press, pp. 577-580.

Levins, R. [1968]. Evolution in Changing Environments: Some Theoretical Explorations. Princeton University Press.

Lomeli, H. et al [1994]."Control of kinetic properties of AMPA receptor channels by nuclear RNA editing." Science. Vol. 266, pp 1709-1713..

Lorenz, K. [1965]. Evolution and Modification of Behavior. Chicago University Press.

Lorenz, K. [1971]."Knowledge, beliefs and freedom." In: Hierarchically Organized Systems in Theory and Practice. P. Weiss (ed.). Hafner.

Lorenz, K. [1981]. The Foundations of Ethoogy. Springer-Verlag.

Mataric, M.J. [1995]."Evaluation of learning performance of situated embodied agents." In: Advances in Artificial Life. F. Moran, A. Moreno, J.J. Merelo, and P. Chacon (eds.). Springer-Verlag, pp. 579-589.

Maturana, H. [1979]."Biology of language: the epistemology of reality." Psychology and Biology of Language and Thought: Essays in honor of Eric Lenneberg. Academic Press, pp. 27-63.

Maturana, H. and F. Varela [1987]. The Tree of Knowledge: The Biological Roots of Human Understanding. New Science Library.

Maynard Smith, J. [1986]. The Problems of Biology. Oxford University Press.

McCulloch, W.S. and W. Pitts [1943]."A logical calculus of the ideas immanent in nervous activity." Bulletin of Mathematical Biophysics. vOL. 5, PP. 115-133.

Medin, D.L. and M.M. Schafer [1978]."A context theory of classification learning." In: Psychological Review. . Vol. 35, pp. 207-238.

Medina-Martins, P. and L. Rocha [1992]."The in and the out: an evolutionary approach." In: Cybernetics and Systems 92. R. Trappl (Ed.). World Scientific Press, pp. 681-689.

Medina-Martins, P., L. Rocha, et al [1993]. CYBORGS: A Fuzzy Conversational System. Final report for the NATO International Program on Learning Systems.

Medina-Martins, P., L. Rocha, et al [1994]."Metalogues: an essay on computers' psychology - from childhood to adulthood." In: Cybernetics and Systems 94. R. Trappl (Ed.). World Scientific Press, pp. 565-572.

Medina-Martins, Pedro [1995]."Metalogues: an abridge of a genetic psychology of non-natural systems." Communication and Cognition - Artificial Intelligence. Vol. 12, Nos. 1-2, pp. 111-156.

Minch, Eric [1995]."The beginning of the End: on the origin of final cause." In: International Seminar on Evolving Systems, Vienna March 1995. G. van de Vijver and S. Salthe (eds.). Kluwer (In Press).

Minsky, M. [1975]."A framework for representing knowledge." In: The Psychology of Computer Vision. P. Winston (ed.). McGraw-Hill.

Mitchell, Melanie [1996a]. An Introduction to Genetic Algorithms. MIT Press.

Mitchell, Melanie [1996b]."Computation in cellular automata: a selected review." In: Nonstandard Computation. H.G. Schuster and T. Gramms (eds.). VCH Verlagsgesellschaft (In Press). Available as Santa Fe Institute Preprint (96-09-074).

Montana, D.J. and L.D. Davis [1989]."Training feedforward networks using genetic algorithms." In: Proceedings of the International Joint Conference on Artificial Intelligence. . Morgan Kaufmann.

Moreno, A., A. Etxeberria, and J. Umerez [1994]."Universality without matter?." In: Artificial Life IV. R. Brooks and P. Maes (eds.). MIT Press, pp. 406-410.

Morris, C.W. [1946]. Signs, Language, and Behavior. G. Braziller Publishers..

Nakamura, K. and S. Iwai [1982]."A representation of analogical inference by fuzzy sets and its application to information retrieval systems." In: Fuzzy Information and Decision Processes. Gupta and Sanchez (Eds.). North-Holland, pp. 373-386.

Nicolis, G. and I. Prigogine [1977]. Self-Organization in Nonequilibrium Systems: From Dissipative Structures to Order through Fluctuations. Wiley-Interscience.

Osherson, D. and E. Smith [1981]."On the adequacy of prototype theory as a theory of concepts." Cognition. Vol. 9, pp. 35-58.

Packard, N. [1988]."Adaptation to the edge of chaos." In: Complexity in Biologic Modelling. S. Kelso and M. Shlesinger (eds.). 21

Papert, S. [1991]."Situating construction." In: Constructinism. I. Harel and S. Papert (eds.). Ablex Publishing.

Pask, Gordon [1975]. Conversation, Cognition, and Learning: A Cybernetic Theory and Methodology. Elsevier.

Pask, Gordon [1976]. Conversation Theory: Applications in Education and Epistemology. Elsevier.

Pask, Gordon [1992]."Different kinds of cybernetics." In: New Perspectives on Cybernetics. G. van de Vijver (ed.). Kluwer, pp.11-31.

Pattee, Howard H. (Ed.) [1973]. Hierarchy Theory: The Challenge of Complex Systems. George Braziller, New York.

Pattee, Howard H. [1978]."The complementary principle in biological and social structures." Journal of Social and Biological Structures. Vol. 1, pp. 191-200.

Pattee, Howard H. [1982]."Cell psychology: an evolutionary approach to the symbol-matter problem." Cognition and Brain Theory. Vol. 5, no. 4, pp. 191-200.

Pattee, Howard H. [1989]."Simulations, realizations, and theories of life." In: Artificial Life. C. Langton (ed.). SFI Series in the Sciences of Complexisty. Addison-Wesley, pp. 63-77.

Pattee, Howard H. [1995a]."Evolving self-reference: matter, symbols, and semantic closure." Communication and Cognition - Artificial Intelligence. Vol. 12, nos. 1-2 (Rocha[1995a]), pp. 9-27.

Pattee, Howard H. [1995b]."Artificial life needs a real epistemology." In: Advances in Artificial Life. F. Moran, et al. Springer-Verlag. pp 23-38.

Piaget, J. [1971]. The Construction of Reality in the Child. Ballantine Books.

Pinker, S. [1993]. The Language Instinct. Morrow.

Pollack, R. [1994]. Signs of Life: The Language and Meanings of DNA. Houghton Mifflin.

Poundstone, W. [1987]. The Recursive Universe. Oxford University Press.

Prem, Erich [1995]."Grounding and the entailment structure in robots and Artificial Life." In: Advances in Artificial Life. F.Moran, A. Moreno, J.J. Merelo, and P. Chacon (eds.). Springer-Verlag, pp. 39-52.

Prigogine, I. [1985]."New perspectives on complexity." In: The Science and Praxis of Complexity. United Nations Library. Reprinted in Klir [1991].

Ramer, A. [1987]."Uniqueness of information measure in the theory of evidence." Fuzzy Sets and Systems. Vol. 24, pp. 183-196.

Ramer, R. [1990]."Concepts of fuzzy information on continuous domains." Int. J. of General Systems. Vol. 17, pp. 241-248.

Ramsey, W.M., S.P. Stich, and D.E. Rumelhart (eds.) [1991]. Philosophy and Connectionist Theory. Lawrence Erlbaum.

Random House, [1994]. Webster's Electronic Dictionary and Thesaurus. WordPerfect Corporation.

Rennie, J. [1993]."DNA's new twists." Scientific American. March 1993.

Resconi, G., G. Klir, U. St.Clair, and D. Harmanec [1993]."On the Integration of Uncertainty Theories." International Journal Of Uncertainty, Fuzziness and Knowledge Based Systems. Vol. 1, No. 1, pp. 1-18.

Riedl, R [1977]."A systems-analytical approach to macro-evolutionary phenomena." Quarterly Review of Biology. Vol. 52, pp. 351-370.

Riedl, R. [1984]. Biology of Knowledge. Wiley.

Rocha, Luis, M. [1991]."Fuzzification of conversation theory." In: . F. Heylighen (Ed.). Paper delivered at the Principia Cybernetica Workshop, Free University of Brussels.

Rocha, Luis, M. [1994a]."Cognitive categorization revisited: extending interval valued fuzzy sets as simulation tools concept combination." Proceedings of the 1994 International Conference of NAFIPS/IFIS/NASA. IEEE Press, pp. 400-404.

Rocha, Luis M. [1994b]."Von Foerster's cognitive tiles: semantically closed building blocks for AI and ALife." In: Cybernetics and Systems' 94. R, Trappl (Ed.). World Scientific Press. pp. 621-628.

Rocha, Luis M. (Ed.) [1995a]. special issue in Self-Reference in Biological and Cognitive Systems of Communication and Cognition - Artificial Intelligence. Vol. 12 nos. 1-2.

Rocha, Luis M. [1995b]."Artificial semantically closed objects." Communication and Cognition - Artificial Intelligence. . Vol. 12, nos 1-2, (Rocha[1995a]) pp. 368-382.

Rocha, Luis M. [1995c]."Contextual genetic algorithms: evolving developmental rules." In: Advances in Artificial Life. J. Moran, A. Moreno, J.J. Merelo, and P. Chacon (Eds.). Springer -Verlag, pp. 368-382.

Rocha, Luis M. [1995d]."Interval based evidence sets." Proc. of ISUMA-NAFIPS'95. IEEE Press, pp. 624-629.

Rocha, Luis [1995e]. Evolutionary Systems and Artificial Life - Lecture Notes. WWW Document. http://ssie.binghamton.edu/~rocha/alife.html.

Rocha, Luis M. [1995f]."Selected self-organization: from eigenbehavior to descriptions." In: Proceedings of the International Seminar on Evolving Systems, Vienna 1995. S. Salthe and G. Van de Vijver. Kluwer. (in press).

Rocha, Luis M. [1996a]."Eigenbehavior and symbols." Systems Research. Vol. 13, No. 3, pp. 371-384.

Rocha, Luis M. [1996b]."Relative uncertainty: measuring uncertainty in discrete and nondiscrete domains." In: Proccedings of the NAFIPS'96. M. Smith et al (Eds.). IEEE Press. pp. 551-555.

Rocha, Luis M. [1997a]."Relative uncertainty and evidence sets: a constructivist framework." International Journal of General Systems. Vol. 25. (In Press).

Rocha, Luis M. [1997b]."Evidence Sets: Contextual Categories." In: Semiotics and Control of Complex Systems. M. Coombs and J. Casti (Eds.). Santa Fe Institute Series in the Sciences of Complexity. Addison-Wesley. (In Press).

Rocha, Luis M. [1997c]."Interval based evidence sets: modeling subjective categories." International Journal of General Systems. In Press.

Rocha, Luis M. [1997d]."Fuzzy Development Programs: Emergent Classification and Embodied Genetic Algorithms." Evolutionary Computation. (Submitted).

Rocha, Luis M., V. Kreinovich, and K. B. Kearfott [1996]."Computing uncertainty in interval based sets." In: Applications of Interval Computations. V. Kreinovich and K.B. Kearfott (Eds.). Kluwer Academic Publishers, pp. 337-380.

Rosch, E. [1975]."Cognitive representations of semantic categories." J. of Experimental Psychology. Vol. 104, pp. 27-48.

Rosch, E. [1978]."Principles of categorization." In: Cognition and Categorization. E. Rosch and B. Lloyd (Eds.). Hillsdale, pp. 27-48.

Rosen, Robert [1985]. Anticipatory Systems. Pergamon Press.

Rosen, Robert [1991]. Life Itself. Columbia University Press.

Rosen, Robert [1993]."Bionics revisited." In: The Machine as a Metaphor and Tool. H. Haken, A. Karlqvist, and U. Svedin (eds.). Springer-Verlag, pp. 87-100.

Rosen, Robert [1995]."The mind-brain problem and the physics of reductionism." Communication and Cognition - Artificial Intelligence. Vol. 12, nos. 1-2 (Rocha[1995a]) pp. 29-43.

Rumelhart, D. [1975]."Notes on a schema for stories." In: Representation and Understanding: Studies in Cognitive Science. D.Bobrow and A. Collins (eds.). Academic Press, pp. 211-236.

Salthe, Stanley N. [1985]. Evolving Hierarchical Systems. Columbia University Press.

Salthe, Stanley N. [1991]."Varieties of Emegence." World Futures. Vol. 32, pp. 69-83.

Salthe, Stanley N. [1993]. Development and Evolution: Complexity and Changes in Biology. MIT Press.

Salthe, Stanley N. [1995]."A Peircean semiotic interpretation of development." Ludus Vitalis. Vol. 3, No. 4, pp. 15-228.

Schum, D.A. [1994]. Evidential Foundations of Probabilistic Reasoning. John Wiley and Sons.

Seiwart, S.D. and K. Stuart [1994]."RNA Editing: transfer of genetic information from gRNA to precursor mRNA in Vitro." Science. Vol. 226, pp. 114-116.

Shafer, G. [1976]. A Mathematical Theory of Evidence. Princeton University Press.

Shafer, G. and J. Pearl (Eds.) [1990]. Readings in Uncertain Reasoning. Morgan Kauffman.

Simpson, L. and D. Maslov [1994]."RNA editing and the evolution of parasites." Science. Vol. 264, pp. 1870-1871.

Smith, E.E. and D.L. Medin [1981]. Categories and Concepts. Harvard University Press.

Smith, E. and D. Osherson [1984]."Conceptual combination with prototype concepts." Cognitive Science. Vol. 8, pp. 337-361.

Stuart, K. [1993]."RNA editing in mitochondria of african trypanosomes." In: RNA Editing : The Alteration of Protein Coding Sequences of RNA. R. Benne (Ed.). Ellis Horwood. pp. 26-52.

Sturn, N.R. and L. Simpson [1990]."Kinetoplast DNA minicircles encode guide RNA's for editing of cytochrome oxidase subunit III mRNA." Cell. Vol. 61, pp.879-884.

Thom, R. [1976]. Structural Stability and Morphogenesis: An Outline of a General Theory of Models. Benjamin/Cummings Publishing.

Tinbergen, N. [1951]. The Study of Instinct. Clarendon Press.

Turksen, B. [1986]."Interval valued fuzzy sets based on normal forms." Fuzzy Sets and Systems. Vol. 20, pp. 191-210.

Turksen, B. [1994]."Interval valued fuzzy sets and fuzzy measures." Proc. of the NAFIPS/IFIS/NASA '94. IEEE Press, pp. 317-321.

Turksen, I.B. [1996]."Non-specificity and interval-valued fuzzy sets." Fuzzy Sets and Systems. Vol. 80, pp. 87-100.

Umerez, Jon [1995]."Semantic Closure: a guiding notion to ground Artificial Life." In: Advances in Artificial Life. F. Moran, A. Moreno, J.J. Merelo, and P. Chacon (eds.). Springer-Verlag, pp. 77-94.

van Gelder, Tim [1991]."What is the 'D' in 'PDP': a survey of the concept of distribution." In: Philosophy and Connectionist Theory. W. Ramsey et al. Lawrence Erlbaum.

Varela, F. [1979]. Principles of Biological Autonomy. Elsevier North-Holland.

Varela, F. E. Thompson, and E. Rosch [1991]. The Embodied Mind: Cognitive Science and Human Experience. MIT Press.

Varela, F.J. and P. Bourgine [1992]. Towards a Practice of Autonomous Systems: Proceedings of the First European Conference on Artificial Life. MIT Press.

Vejnarová, J. and G.J. Klir [1993]."Measure of strife in Dempster-Shafer Theory." International Journal of General Systems. Vol. 22, pp. 25-42.

von Glasersfeld, E. [1995]. Radical Constructivism: A Way of Knowing and Learning. The Falmer Press.

von Foerster, H. and G.W. Zopf (eds.) [1962]. Principles of Self-Organization. Pergamon Press.

von Foerster, Heinz [1960]."On self-organizing systems and their environments." In: Self-Organizing Systems. M.C. Yovits and S. Cameron (eds.). Pergamon Press, pp. 31-50. Reprinted on von Foerster [1981], pp. 2-22.

von Foerster, Heinz [1965]."Memory without record." In: Anatomy of Memory. D.P. Kimble (ed.). Science and Behavior Books, pp. 388-433. Reprinted in von Foerster [1981], pp. 91-137.

von Foerster, Heinz [1969]."What is memory that it may have hindsight and foresight as well?." In: The Future of the Brain Sciences. S. Bogoch (ed.). Plenum Press, pp. 1965 and 89-95.

von Foerster, Heinz [1977]."Objects: tokens for (eigen-)behaviors." In: Hommage a Jean Piaget: Epistemologie Genetique et Equilibration. B. Inhelder, R. Gracia, and J. Voneche (Eds.). Delachaux et Niestel. Reprinted in von Foerster [1981], pp. 274-285.

von Foerster, Heinz [1981]. Observing Systems. Intersystems Publications.

von Neumann, J. [1966]. The Theory of Self-Reproducing Automata. University of Illinois Press.

Waddington, C.H. [1972]."Postcript." In: Towards a Theoretical Biology. C.H. Waddington (ed). Endinburgh University Press.

Wang, Z. and G. Klir [1992]. Fuzzy Measure Theory. Plenum Press.

Way, Eileen C. [1991]. Knowledge Representation and Metaphor. Kluwer.

Weaver, W. [1848]."Science and complexity." American Scientist. Vol. 36, pp. 536-544. Reprinted in Klir [1991], pp. 449-456.

Wiener, N. [1961]. Cybernetics. MIT Press. Second Edition. (first edition 1948).

Wilson, D.S. and E. Sober [1994]."Re-introducing group selection to the human behavioral sciences." Behavior and Brain Sciences. Vol. 17, pp. 585-654.

Wilson, D.S. and A. Wells [1995]."Radical epistasis and the genotype-phenotype relationship." Artificial Life. Vol. 2, no.1, pp. 117-128.

Wilson, S.W. [1988]."The genetic algorithm and simulated evolution." In: Artificial Life. C.G. Langton (ed.). SFI Studies in the Sciences of Complexity. Addison-Wesley, pp. 157-166.

Wuketis, F.M. [1990]. Evolutionary Epistemology and Its Implications for Humankind. State University of New York Press.

Yager, R.R. [1979]."On the measure of fuzziness and negation. Part I: membership in the unit interval." Int. J. of General Systems. Vol. 5, pp. 221-229.

Yager, R.R. [1980]."On the measure of fuzziness and negation: Part II: lattices." Information and Control. Vol. 44, pp. 236-260.

Yager, R.R. [1982]."An introduction to applications of possibility theory." Human Systems Management. Vol. 3, pp. 246-269.

Yager, R.R. [1983]."Entropy and specificity in a mathematical theory of evidence." Int. J. of General Systems. Vol. 9, pp. 249-260.

Yen, John [1990]."Generalising the Dempster-Shafer theory to fuzzy sets." IEEE Transactions on Systems, Man, and Cybernetics. Vol. 20, pp. 559-570.

Yuan, Bo, W. Wua, and Y. Pan [1994]."On normal form based interval valued fuzzy sets and its application to approximate reasoning." International Journal of General Systems. .

Zadeh, Lofti A. [1965]."Fuzzy Sets." Information and Control. Vol. 8, pp. 338-353.

Zadeh, Lofti A. [1971]."Quantitative fuzzy semantics." Informations Sciences. Vol. 3, pp. 159-176.

Zadeh, Lofti A. [1975]."The concept of a linguistic variable and its application to approximate reasoning, I, II, and III." Information Sciences. Vol. 8, pp. 199-249;301-357, Vol. 9, pp. 43-80.

Zadeh, Lofti A. [1978]."PRUF-a meaning representation language for natural languages." Int. J. of Man-Machine Studies. Vol. 10, pp. 383-410.

Zeleny, M., G. Klir, and K. Hufford [1989]."Precipitation membranes, osmotic growths, and synthetic biology." In: Artificial Life. C. Langton (ed.). SFI Studies in the Sciences of Complexity. Addison-Wesley, pp. 125-155.

Zhu, Q. and E.S. Lee [1995]."Evidence theory in multivalued logic systems." Int. J. of Intelligent Systems. Vol. 10, pp. 185-199.

Zimmerman, H. and P. Zysno [1980]."Latent connectives in human decision making." Fuzzy Sets and Systems. Vol. 4, pp. 37-51.

1. This subsection follows essentially my introduction to the special edition of Communication and Cognition - Artificial Intelligence, Self-Reference in Biological and Cognitive Systems [Rocha, 1995a, page 3-8].

2. The ideas presented in this section were first developed in Rocha [1995c, 1995f, 1996a, 1997d], as well as on the lecture notes for the course "Evolutionary Systems and Artificial Life" [Rocha, 1995e].

3. The structure of a dynamical system refers to the actual components and interrelations between components that establish the dynamics.

4. Causal in the sense that self-organization is considered to have exclusively a material substrate with no other processes are involved. It is not the scope of the present work to dwell into the issues of causation. Those who are more satisfied with Aristotelian classes of causation [e.g. Rosen, 1991, Minch, 1995], will find the previous expression vexed as material causality does not imply final causality. I thank Stan Salthe for pointing this out.

5. Homuncular explanation occurs when "we explain the capacities of the overall system by adverting to the capacities of its components, and the way they interrelate" [Clark, 1996, page 263]

6. More on the coupling of dynamical systems and evolutionary algorithms to achieve higher discriminative power in chapter 5.

7. I am thinking more of machine learning here. It can be argued that human learning is based on a more implicit developmental, Piagetian, process [Pask, 1977]. Such a discussion is largely beyond the scope of the present work, but will be given larger attention in section 2 of this chapter.

8. In the genetic system there are 4 nucleotides (adenine, guanine, cytosine, and thymine/uracil), since each aminoacid is coded by 3 nucleotides, codons, there are 4³ = 64 possible combinations of these, which makes the genetic code degenerate with only 20 aminoacids.

9. To appreciate the dimensions of such a combinatorial universe, consider the often used [Eigen, 1992] sequence space devised by Hamming [1980] for a linear sequence of symbols. A sequence of dimension n, where each position can take 2 values (note that DNA actually has 4 values possible for each position), forms a hypercube of n dimensions where each corner represents a possible sequence. There are 2ⁿ possible sequences.

10. As introduced by Howard Pattee in the Biological Systems course materials.

11. Memory tokens, as discussed previously, can be either distributed or local. In the local case, they can be referred to as symbols.

12. From unpublished personal communication .

13. For instance, "homing", "safe-wondering", "resting" as in Majaric's robots.

14. Systemic contexts because all social ecological interactions are defined as self-organizing systems.

15. The material in this subsection reflects work published in [Henry and Rocha, 1996] and [Rocha, 1997a, 1997c]

16. The material in this chapter has been previously published in Rocha [1994a, 1995d, 1996b, 1997a, 1997b, 1997c], Rocha, Kreinovich and Kearfott [1996] and Henry and Rocha [1996].

17. An example of a radial category [after Lakoff, 1987] is the category of mother. A listing of core properties to be considered a member of this category, coherent in the context of birth, would be, for instance: woman who gives birth, raises, nurtures, educates a child. However, members of the category of mother exist which do no obey such listing: adoptive mother, surrogate mother, genetic mother, etc. These members do not obey the list, or obey it only to a very small degree; however, though not prototypes, they are elements of the category mother. They are also not random elements, but are unpredictable until a different context is introduced.

18. A -algebra is a class of X that contains X and is closed under the formation of complements and countable unions.

19. To visualize this, consider an "L" shaped focal element of X � Y, its projections R_X and R_Y will be the same as those of a focal element given by a rectangle with the same width and length as the L-shaped one. The rectangle clearly contains the "L"-shaped focal element.

20. This is the definition of a standard fuzzy set. Other types of fuzzy sets exist, some of which are introduced throughout this chapter. In the following, unless otherwise noticed, the name fuzzy set refers to this definition of standard fuzzy set.

21. Notice that both crisp and fuzzy sets capture nonspecificity in the cardinality of their elements. The inclusion of nonspecificity discussed here is in the formalization of their membership degrees, which in this sense, represents a second-order nonspecificity.

22. Possibility understood as the truth-value representation of fuzzy logic propositions, not to normalized possibility distributions in the current interpretations of possibility theory [de Cooman et al, 1995].

23. Triangular norms (t-norms) and triangular conorms (t-conorms) are the general names given to the families of fuzzy intersections and unions respectively. Those t-norms that uniquely determine a dual t-conorm, and vice versa are referred to as conjugate pairs of t-norms and t-conorms.

24. This idea of interpreting bodies of evidence as perspectives, spins off from a generalization of Gordon Pask's [1975, 1976] Conversation Theory which I have proposed with the construction of a data-retrieval system to be discussed in chapter 5 [Medina-Martins and Rocha, 1992].

25. That is, every element of the set is formally free to be ascribed any value in the unit interval, independently of the values of other elements in the set.

26. Inclusion in DST was discussed in section 2.2.6.

27. Note that the bodies of evidence considered here, and throughout the paper, have a finite number of focal elements (see section 2.2.3).

28. Since we desire positive measures of information.

29. �(A) �(B) when A B.

30. Nonspecificity measure (20) is in some ways similar to Yager's [1982, 1983] specificity. However, Yager's measure deals with the intuitive inverse of nonspecificity, but in absolute terms. Even though it is restricted to the unit interval, the specificity content of a body of evidence is independent on the size of its universal set.

31. The material presented in this chapter has been previously published in Rocha [1995c, 1995f, 1997d],

32. Discrete type variables can also of course be represented in FDP's as fuzzy sets can be defuzzified into crisp sets. An example is discussed in chapter 5.

33. Some of the work presented in this section was first presented in Rocha[1991].

34. Nakamura and Iwai's work has been expanded formally and in its interpretation from its original form.

35. This measure of distance calculated in a large network of nodes, is usually not a Euclidean metric because it does not observe the triangular inequality. In other words, the shortest distance between two nodes of the network might not be the direct path. This means that two nodes may be closer to each other when another node is associated with them. Such measures of distance are referred to as semi-metrics [Galvin and Shore, 1991]. For the purposes of the work here presented, we do not need to worry about the mathematical significance of semi-metrics.

36. In general, it is still much easier to recalculate the distance of the n-reachable concepts to a new concept in a database, than to completely retrain a neural network.

37. Portions of the work here presented were published in Rocha [1997d]

38. These patterns were obtained from Don Gause with his permission from the data files of the Neural Network and Genetic models class.

39. Other values of these probabilities were tried, as well as other fitness functions. The set of parameters described above proved to be the most efficient.

40. This work has been mainly pursued by the Adaptive Computation Group of the Santa Fe Institute, whose members I am indebted to for many conversations on this problem. I particularly wish to thank Melanie Mitchell and Wim Hordijk for making many of their unpublished research available to me, without which I would not be able tackle the problem.

41. This fitness is not the same as the one used in the GA. The latter uses IC's whose density of ON's is uniformly distributed in the unit interval, while the former is the so-called unbiased fitness. It is computed by randomly flipping each bit of the IC's with equal probability. This results in densities closer to 0.5 which are the toughest for the rule to tackle.